
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сумісна дія згинання та кручення для стержнів круглого або кільцевого перерізуСодержание книги
Поиск на нашем сайте
У сучасних силових пристроях широко використовується вали – циліндричні стержні круглого або кільцевого перерізів, за допомогою яких передається та розподіляється потужність (крутний момент) між елементами механічної системи. Навантаження на вали з боку зубчатих коліс, натягу ременів, власної ваги вала та шківів спричиняють просторове згинання і кручення, чи складне згинання, кручення та розтягання (стискання). Тому у поперечних перерізах валів виникають такі внутрішні силові фактори: Отже, в будь-якому перерізі можуть одночасно виникнути нормальні напруження Зазначимо, що у даному випадку, як і при складному згинанні, впливом дотичних напружень від поперечних сил можна знехтувати по зрівнянню з дотичними напруженнями, спричиненими крученням. Якщо відсутні і поздовжні сили Згинальні і крутний моменти діють у трьох взаємно - ортогональних площинах. Якщо площина дії моменту проходить крізь вісь балки, то такий момент є згинальним. Моменти, що діють у площині, ортогональній до осі вала, приводять к його крученню. Наступним кроком до вирішення задачі є визначення небезпечного перерізу. Для круглого та кільцевого профілів ця операція спрощується завдяки променевій симетрії перерізу. Оскільки усі осі, які проходять крізь центр ваги кола або кільця, є головними, то просторове згинання можна завжди звести до плоского, у площині дії сумарного згинального моменту
Це легко пояснити, якщо згадати визначення вектора-моменту
Рисунок 26
Величина цього вектора дорівнює діючому моменту, а його напрям ортогональний до площини, у якій розташований момент. Вектор – момент має додатне значення, якщо дивлячись з кінця цього вектора, обертання пари сил здійснюється проти годинникової стрілки. Розглянемо, наприклад, переріз вала, і позначимо внутрішні моменти (рис. 27).
Рисунок 27
Побудуємо вектори – моменти
Площина дії сумарного згинального моменту
де Розподіл дотичних напружень від дії крутного моменту у тому ж перерізі наведений на рис. 28.
Рисунок 28
Розподіл
де Таким чином, у точках 1,2 маємо збіг найбільших нормальних та дотичних напружень. Напружений стан у цих точках – двохвісний (плоский) Будемо вважати, що матеріал вала є пластичним, до якого можна застосувати ІІІ або ІV гіпотезу міцності. Тоді формули умови міцності для плоского напруженого стану мають такий вигляд:
Використовуючи (38) та (39) отримаємо
Вирази (41) свідчать, що розрахунок круглих та кільцевих валів при сумісній дії згинання та кручення формально зводиться до розрахунку на „просте згинання” під дією еквівалентного моменту
Таким чином, для визначення найбільш небезпечного перерізу слід зробити лише ряд розрахунків. Згідно з (42) треба підрахувати величини еквівалентних моментів у всіх потенційно небезпечних перерізах. Найнебезпечніший з них має максимальний еквівалентний момент. Зазначимо також, що знаки складових моментів (їх напрям) у виразах (42) не мають особливого значення, тому при підрахунках, перш за все треба звертати увагу до перерізів з максимальними за модулем компонентами.
Приклад 5 Розглянемо випадок складного опору на прикладі розрахунку діаметру вала редуктора (рис 29). Нехай вал редуктора передає потужність
Рисунок 29
Для того щоб зробити розрахунки напружено-деформованого стану будь-якої деталі, треба визначити розподіл внутрішніх силових факторів в перерізах цієї деталі. Тому, зовнішні навантаження у вигляді сил та моментів, що не діють безпосередньо на розрахунковий об’єкт, треба спочатку привести до центру ваги відповідних перерізів деталі. Якщо деталь знаходиться у складі механізму, враховуються лише ті навантаження, що діють саме на позначену деталь з боку інших відкинутих складових частин механізму. Тому у формуванні розрахункової схеми мають бути задіяні як активні, так і реактивні зусилля. Так тангенціальні сили Усі прикладені сили діють на відстані радіусів відповідних шківів від центрів ваги валу, який підлягає розрахунку. Тож треба перенести ці сили до валу за допомогою паралельного переносу. Розглянемо цей процес більш детально. У точці С такий перенос треба зробити двічі (рис. 30).
Рисунок 30
Перенос сили
Аналогічно, після переносу сили
Площину дії моментів Алгебраїчно сумуючи силові фактори у точці С, маємо:
Аналогічна процедура застосовується до сил
Рисунок 31 де
Повна розрахункова схема валу ОВСDЕ зображена на рис. 29. Крутні моменти Таким чином маємо сумісну дію кручення та складного згинання, що розкладається на два прості згинання у головних площинах валу (рис. 29). Оскільки зусилля
З умов задачі 100 % потужності (крутного моменту) розподіляється між веденими шківами Е і О у відношенні 1:3 (25 %: 75 %), отже
Таким чином у площині
По знайдених крутних моментах можна побудувати епюру. У перерізах а у перерізах З співвідношень (43), (44) визначаємо окружні зусилля
Для побудови епюри згинального моменту
Згинальні моменти в перерізах вала підраховуються наступним чином:
Аналогічну процедуру можна застосувати до побудови епюри згинального моменту
У перерізі
Небезпечний переріз визначаємо по найбільшому значенню еквівалентного моменту (42). У нашому випадку для перерізу С
або
Для підрахунку діаметру використаємо, наприклад, ІІІ гіпотезу міцності (41)
Після округлення діаметру до найближчого стандартного значення маємо: Відомо, що різниця між ІІІ та ІV гіпотезами міцності не перевершує сімох відсотків у тому випадку, якщо у перерізі діють лише дотичні напруження. У даному прикладі, підрахунок діаметру згідно ІV гіпотези міцності дає приблизно ті ж самі результати.
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 667; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.4.50 (0.006 с.) |

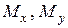 – згинальні моменти,
– згинальні моменти, 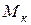 – крутний момент,
– крутний момент, 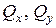 – поперечні зусилля,
– поперечні зусилля, 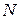 – поздовжня сила.
– поздовжня сила. , а також дотичні напруження
, а також дотичні напруження 

 .
.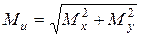 (38)
(38) пари сил (рис. 26).
пари сил (рис. 26).

 та
та  . Згідно з їх визначенням, обидва вектори мають розташування у площині перерізу
. Згідно з їх визначенням, обидва вектори мають розташування у площині перерізу  і можуть бути складеними у геометричну суму згідно (38). Кожен з цих векторів співпадає за напрямом з нейтральною лінією власного моменту, тому вектор-момент
і можуть бути складеними у геометричну суму згідно (38). Кожен з цих векторів співпадає за напрямом з нейтральною лінією власного моменту, тому вектор-момент  вказує спільну нейтральну лінію від одночасної дії обох згинальних моментів
вказує спільну нейтральну лінію від одночасної дії обох згинальних моментів 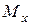 та
та 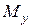 . Нахил нейтральної лінії визначається кутом
. Нахил нейтральної лінії визначається кутом 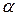
 .
. ортогональна до спільної нейтральної лінії. Точки 1 та 2, що лежать у площині моменту
ортогональна до спільної нейтральної лінії. Точки 1 та 2, що лежать у площині моменту  , (39)
, (39) – осьовий момент опору кола.
– осьовий момент опору кола.
 свідчить, що в контурних точках 1 та 2 діють однакові максимальні дотичні напруження
свідчить, що в контурних точках 1 та 2 діють однакові максимальні дотичні напруження , (40)
, (40) – полярний момент опору кола.
– полярний момент опору кола. ,
,  , тому для запису умови міцності треба використати відповідну гіпотезу міцності.
, тому для запису умови міцності треба використати відповідну гіпотезу міцності.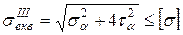 , або
, або 
 (41)
(41) (42)
(42)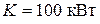 , яка розподіляється між веденими шківами у співвідношенні 1:3, і обертається з кутовою швидкістю
, яка розподіляється між веденими шківами у співвідношенні 1:3, і обертається з кутовою швидкістю 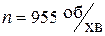 . Допустиме напруження матеріалу вала
. Допустиме напруження матеріалу вала  .
.

 і
і  (рис.29) є реакціями, діючими на ведені шківи О і Е відповідно, з боку відкинутих сателітів. Активні зусилля
(рис.29) є реакціями, діючими на ведені шківи О і Е відповідно, з боку відкинутих сателітів. Активні зусилля  і
і  прикладені до ведучого шківа С безпосередньо від гілок ремінної передачі.
прикладені до ведучого шківа С безпосередньо від гілок ремінної передачі.
 до центра ваги вала на відстань
до центра ваги вала на відстань 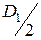 супроводжується появою моменту
супроводжується появою моменту  .
.
 у зворотному напрямку
у зворотному напрямку .
.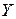 ), другий напрямок – плече переносу (вісь
), другий напрямок – плече переносу (вісь 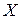 ). Тому площина дії обох моментів
). Тому площина дії обох моментів  . Звісно, що у цій площині моменти діють відносно осі
. Звісно, що у цій площині моменти діють відносно осі 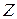 , що підкреслюється індексами моментів.
, що підкреслюється індексами моментів. (43)
(43) і
і 
 (44)
(44) ,
, 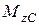 ,
,  приводять до кручення в площині
приводять до кручення в площині  згинають вал у площині
згинають вал у площині 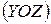 , а поперечна сила
, а поперечна сила 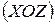 .
. . (45)
. (45)

 крутний момент дорівнює:
крутний момент дорівнює:  ,
, :
:  .
. (46)
(46) у площині
у площині  .
.





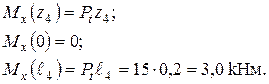
 згинальний момент
згинальний момент 
 згинальний момент відсутній взагалі
згинальний момент відсутній взагалі  , а в перерізі
, а в перерізі  момент є лінійною функцією реакції
момент є лінійною функцією реакції  . Він змінюється від нульового значення у точці, де прикладена сила (плече сили дорівнює нулю), до значення моменту на суміжному інтервалі, тобто
. Він змінюється від нульового значення у точці, де прикладена сила (плече сили дорівнює нулю), до значення моменту на суміжному інтервалі, тобто

 .
. (47)
(47)



