Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Позацентрове розтягання – стискання брусаСодержание книги
Поиск на нашем сайте Окремим випадком сумісної дії згинання та розтягання (стискання) є так зване позацентрове розтягання (стискання). Такий вид складного опору має місце, якщо на брус довільного перерізу діє сила Для того щоб зробити висновки щодо напружено – деформованого стану бруса необхідно привести позацентрову силу
Рисунок 18
Приведення сили
Рисунок 19
Спочатку перенесемо силу Наступним кроком є перенос сили Момент Таким чином в центрі ваги перерізу діють три силові фактори:
Із виразів (27) випливає незмінність внутрішніх зусиль уздовж осі Отже, напружений стан у довільній точці перерізу В складається з напружень від поздовжньої сили
де Для пошуку небезпечної точки у разі складного профілю перерізу, треба побудувати нейтральну лінію. Небезпечною буде точка, найвіддаленіша від нейтральної лінії. Оскільки нейтральна лінія, за її визначенням, є геометричним місцем точок з нульовими напруженнями
де Рівняння нейтральної лінії
Відрізки, що відсікає нейтральна лінія на координатних осях, відповідно дорівнюють
Співвідношення (30) також можна здобути із (24) за допомогою підстановки (27). Треба зазначити, що формули (24) мають більш широкий спектр дії, ніж (30). Наприклад, якщо до конструкції прикладено декілька позацентрових навантажень, то поздовжня сила Із залежностей (30) випливає, що нейтральна лінія перетинає координатні осі в точках, які належать квадрантам, протилежним тому, де знаходиться полюс Р (рис. 20).
Рисунок 20
Якщо проведемо паралельно до нейтральної лінії дотичні до контуру перерізу в обидва боки, знайдемо найбільш напружені точки K та L у розтягнутій і стислій зонах перерізу відповідно (рис. 20). Якщо позначити
З урахуванням (27) умови (31) тотожні умовам (20). Тому, при різних формах перерізів і властивостей матеріалу, в разі позацентрового розтягання (стискання) треба користуватися раніше наведеними сполученнями (20-21.2). Аналізуючи співвідношення (30) можна дістати висновку, що нейтральна лінія не завжди перетинає переріз та не проходить через центр ваги перерізу. Якщо полюс співпадає з центром ваги ( Отже, ядром перерізу називають замкнену зону навколо центра ваги перерізу, яка має таку властивість: якщо позацентрове навантаження розміщене в зоні ядра, то нормальні напруження в усіх точках перерізу мають однакові знаки. Для побудови ядра перерізу задаються різними положеннями нейтральної лінії, дотичними до контуру перерізу, і обчислюють за допомогою (30) координати відповідних граничних точок ядра (точок, до яких має бути прикладена позацентрова сила)
При обертанні нейтральної лінії навколо фіксованої точки контуру перерізу, полюс переміщується вздовж прямої лінії.
Приклад 4 Як приклад розрахунків на позацентрове розтягання (стискання), доберемо допустиме значення сили
Рисунок 21
Для проведення розрахунків на позацентрове розтягання (стискання) першочергово необхідно визначити геометричні характеристики поперечного перерізу відносно головних центральних осей інерції (осьові моменті інерціїї, радіуси інерції, площу перерізу). Спочатку для складного перерізу бруса визначаємо положення центру ваги. Для цього складний профіль переріза розіб’ємо на два прямокутника з власними центральними осями Залишається визначити розташування центру ваги вздовж осі
де
Рисунок 22
Для застосування формули (33) треба обрати опорну вісь
Отриманий результат відкладаємо від опорної осі Сумарна площа перерізу визначається як алгебраїчна сума площ окремих частин:
Осьові моменти інерції перерізу відносно головних центральних осей інерції визначаються за виразами [1]:
де
У системі головних центральних осей інерції полюс (точка, де прикладена сила Наступним кроком до вирішення задачі має бути приведення сили
Рисунок 23
Таким чином маємо:
Силові фактори (35) діють у будь-якому перерізі колони і призводять до появи нормальних напружень, розподіл яких приведено на рис. 23. З цього розподілу витікає, що точки першого квадранту (де розташований полюс) мають напруження одного знаку (від’ємні). То ж нейтральна лінія має пройти крізь другий, третій та четвертий квадранти (рис. 24).
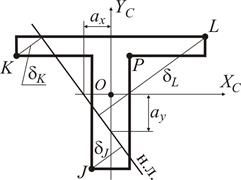
Рисунок 24.
Згідно (30) підрахуємо відрізки
Таким чином, рівняння нейтральної лінії згідно з (29) стає:
або після алгебраїчних перетворень доведемо його до стандартного виду
Нейтральна лінія розподіляє переріз на дві зони. У зоні стискаючих напружень найбільш віддаленою є кутова точка Питання про найбільшу відстань від нейтральної лінії для точок а) графічно викреслити у відповідному масштабі переріз колони, провести нейтральну лінію з урахуванням відрізків б) визначити за допомогою співвідношень аналітичної геометрії найкоротші відстані від точок
де
Знак перед радикалом у знаменнику є протилежним до знаку коефіцієнта С [2]. Наприклад, для точки
для точки
Таким чином, найвіддаленішою точкою в розтягнутій зоні є точка в) записати умови міцності у розтягнутій зоні як для точки
З урахуванням (35)
Звідси вираховуємо допустимі зусилля:
Якщо записати умови міцності для точки
Цей результат ( З отриманих допустимих навантажень згідно з умовами міцності обираємо найменшу силу Для побудови ядра перерізу треба зробити нейтральну лінію дотичною до усіх контурних точок, але так, щоб вона не перетинала площу перерізу (рис. 25).
Рисунок 25
У кожному положенні нейтральної лінії слід підрахувати координати відповідного полюсу, згідно з (32). Так у положенні 1
У положенні 2
У положенні 3
Положення 4 симетрично відносно положення 2, тому
Поворот нейтральної лінії на 90 градусів супроводжується переміщенням полюса по прямим лініям 1–2, 2–3, 3–4, 4–1 (рис. 25).
|
||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 850; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.008 с.) |

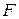 , паралельна до осі бруса Z, що прикладена у точці Р, яка не співпадає з центром ваги перерізу (рис.18). Точку Р з координатами
, паралельна до осі бруса Z, що прикладена у точці Р, яка не співпадає з центром ваги перерізу (рис.18). Точку Р з координатами  називають полюсом, а найкоротшу відстань від неї до центру ваги перерізу – ексцентриситетом
називають полюсом, а найкоротшу відстань від неї до центру ваги перерізу – ексцентриситетом  .
.

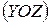 на відстань
на відстань  з точки P до точки С. У площині переносу з’являється момент
з точки P до точки С. У площині переносу з’являється момент 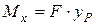 .
.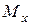 ) на відстань
) на відстань 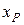 з точки С до точки О. Цей перенос здійснюється у площині
з точки С до точки О. Цей перенос здійснюється у площині 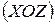 , тому в точці О з’являється момент
, тому в точці О з’являється момент  .
. (27)
(27)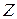 . У разі позацентрового розтягання (стискання) усі перерізи стержня є рівнонебезпечними.
. У разі позацентрового розтягання (стискання) усі перерізи стержня є рівнонебезпечними.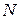 та напружень від чистого згинання моментами
та напружень від чистого згинання моментами 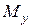 згідно з (19) та з урахуванням (27)
згідно з (19) та з урахуванням (27) , (28)
, (28) – радіуси інерції відносно головних осей перерізу X та Y відповідно.
– радіуси інерції відносно головних осей перерізу X та Y відповідно.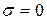 , то з (28) випливає
, то з (28) випливає
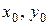 – координати точки, що належить до нейтральної лінії.
– координати точки, що належить до нейтральної лінії. (29)
(29) . (30)
. (30)
 та
та 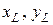 координати точок K і L відповідно, то умови міцності для них мають вигляд:
координати точок K і L відповідно, то умови міцності для них мають вигляд: (31)
(31) ), то нейтральна лінія проходить у нескінченості (напруження розподілені рівномірно по площі перерізу і мають один знак). Із збільшенням ексцентриситету „ е ” нейтральна лінія наближається до перерізу і у певний момент стає дотичною до нього. Таке значення „ е ” вказує на межу ядра перерізу. При подальшому збільшенні ексцентриситету нейтральна лінія перетне переріз і розподілить його на зони з різними знаками напружень (рис. 20). Це важливо для стержнів з крихких матеріалів, що погано чинять опір розтяганню (наприклад, чавун, бетон і т.п.).
), то нейтральна лінія проходить у нескінченості (напруження розподілені рівномірно по площі перерізу і мають один знак). Із збільшенням ексцентриситету „ е ” нейтральна лінія наближається до перерізу і у певний момент стає дотичною до нього. Таке значення „ е ” вказує на межу ядра перерізу. При подальшому збільшенні ексцентриситету нейтральна лінія перетне переріз і розподілить його на зони з різними знаками напружень (рис. 20). Це важливо для стержнів з крихких матеріалів, що погано чинять опір розтяганню (наприклад, чавун, бетон і т.п.).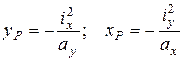 . (32)
. (32)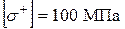 ,
, 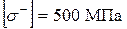 . Розміри перерізу колони наведені на рис. 21.
. Розміри перерізу колони наведені на рис. 21.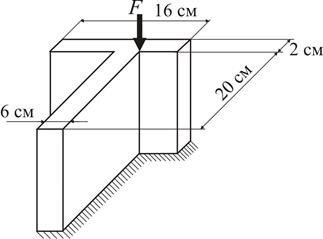
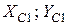 та
та 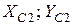 відповідно (рис. 22). Збіг центральних осей
відповідно (рис. 22). Збіг центральних осей 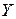 свідчить про наявність симетрії у перерізі. А якщо ось
свідчить про наявність симетрії у перерізі. А якщо ось  .
. (33)
(33)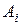 – площа кожної складової перерізу,
– площа кожної складової перерізу,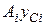 – статичний момент площі, відносно осі
– статичний момент площі, відносно осі 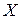 ,
, – координата центра ваги складової площі перерізу.
– координата центра ваги складової площі перерізу.
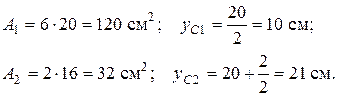
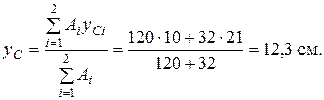
 .
.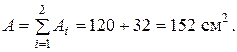
 (34)
(34)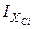 ,
, 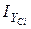 – моменти інерції складової перерізу, підраховані відносно власних центральних осей;
– моменти інерції складової перерізу, підраховані відносно власних центральних осей;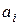 – відстань між осями
– відстань між осями 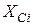 та
та 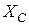 ;
;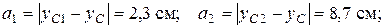
 – відстань між осями
– відстань між осями 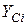 та
та 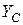 . Для перерізу з віссю симетрії
. Для перерізу з віссю симетрії  ,
, 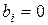
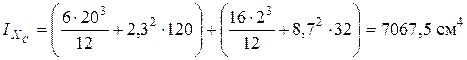 ;
;


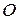 . На рис. 23 в цій точці з’являється окрім сили
. На рис. 23 в цій точці з’являється окрім сили 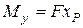 у площині
у площині 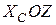 та
та 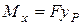 у площині
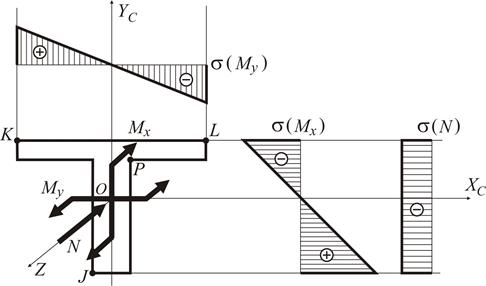
у площині 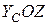 .
.
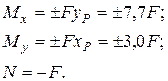 (35)
(35)
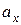 та
та 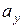 :
: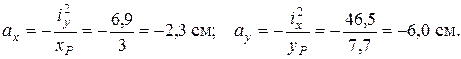

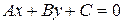 :
: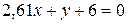 . (36)
. (36) (рис. 24). Найбільш віддаленою точкою у зоні розтягуючих напружень можуть бути кутові точки
(рис. 24). Найбільш віддаленою точкою у зоні розтягуючих напружень можуть бути кутові точки  або
або  , в залежності від нахилу нейтральної лінії до координатних осей
, в залежності від нахилу нейтральної лінії до координатних осей  , (37)
, (37) – найкоротша відстань від точки до прямої,
– найкоротша відстань від точки до прямої, )
)
 )
)
 ) у зоні розтягу, та для т.
) у зоні розтягу, та для т. 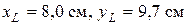 ) – у зоні стискання. При складанні умов міцності сили, моменти та координати точок будемо вважати додатними, а знак напруження приписувати кожному сполучнику, згідно деформації у відповідному квадранті (рис. 23).
) – у зоні стискання. При складанні умов міцності сили, моменти та координати точок будемо вважати додатними, а знак напруження приписувати кожному сполучнику, згідно деформації у відповідному квадранті (рис. 23).


 ), то будемо мати:
), то будемо мати:
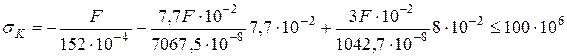

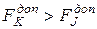 ) вказує, що у розтягнутій зоні найвіддаленіша від нейтральної лінії є дійсно точка
) вказує, що у розтягнутій зоні найвіддаленіша від нейтральної лінії є дійсно точка  .
.