
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика розрахунків на міцністьСодержание книги
Поиск на нашем сайте
У випадку складного деформування стержня, як і у разі простого деформування, стратегічними питаннями є: - визначення небезпечного перерізу; - виявлення в межах цього перерізу небезпечної точки; - формування умов міцності для цієї точки. Для визначення небезпечного перерізуза допомогоюметоду перерізіввиявляють розподіл внутрішніх силових факторів У разі, якщо переріз має форму кола або кільця, небезпечний переріз визначається однозначно за допомогою еквівалентного моменту за будь-якою теорією міцності. Якщо переріз стержня має іншу форму, то може виникнути потреба дослідити декілька потенційно небезпечних перерізів з максимальними комбінаціями внутрішніх силових факторів в різних головних площинах. Визначення небезпечної точки базується у першу чергу на інформації про внутрішні зусилля у перерізі, яку надають епюри Найбільш напружена точка відзначається максимальними значеннями сумарних чи еквівалентних напружень. Формування умов міцності для найбільш напруженої точки залежить від типу її напруженого стану. Якщо в точці мають місце лише нормальні напруження, які сумуються алгебраїчно, то умови міцності набувають вигляду:
аналогічно щодо дотичних напружень
Коли у точці перерізу діють сумісно і нормальні, і дотичні напруження (складний напружений стан), то для запису умови міцності використовується певна гіпотеза міцності. У цьому випадку в точці спочатку треба визначити сумарні компоненти
Наприклад, при використанні гіпотези найбільших дотичних напружень (III гіпотеза міцності)
або гіпотези питомої потенціальної енергії формозміни (IV гіпотеза міцності)
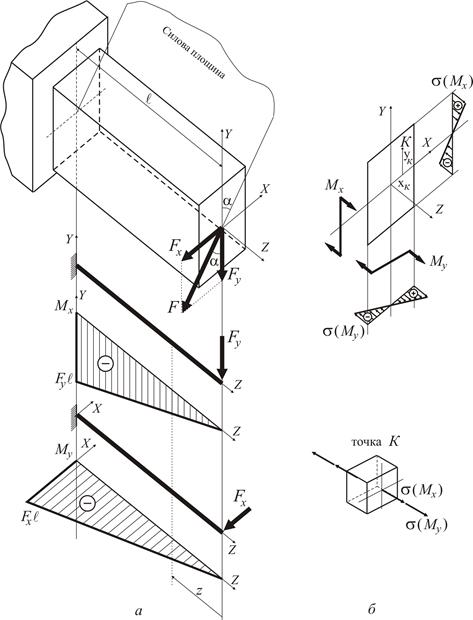
Просторове та косе згинання Згинання називають косим, якщо усі навантаження діють у одній (силовій) площині, яка перетинає вісь балки, але не включає жодної з головних центральних осей інерції перерізу. Якщо силових площин дві і більше, то таке згинання називається просторовим.
Рисунок 1
Розрахунки балок, які знаходяться в умовах косого або складного згинання, можна звести до сумісної дії двох плоских згинань у головних площинах. Для цього навантаження, що діють у довільних силових площинах треба спроектувати до головних площин Треба зазначити, що в даному методичному посібнику ми свідомо не торкаємося питань згинання тонкостінних відкритих профілів (з однією віссю симетрії або без неї), для яких поперечні сили, що проходять крізь центр ваги перерізу, породжують систему неврівноважених дотичних напружень. Останні утворюють крутний момент У практичних розрахунках на міцність для більшості перерізів малими дотичними напруженнями Незважаючи на загальні підходи до рішення задач косого і складного згинання, є деякі відмінності у цих випадках складного опору: а) при косому згинанні деформована вісь бруса є плоскою кривою, а при складному згинанні – просторовою; б) згинальні моменти Розглянемо жорстко затиснуту консольну балку, навантажену на вільному кінці силою Розкладемо зусилля
Рисунок 2
У довільному перерізі
Максимальні значення вони набувають у перерізі
Обчислимо напруження в точці
Оскільки тип напружень від дії згинальних моментів
Усі складові співвідношень (5) (згинальні моменти та координати) будемо вважати додатними, а знак приписувати кожному сполучнику окремо, зважаючи на деформації у відповідному квадранті. Аналізуючи розподіл нормальних напружень у перерізі (рис. 2б), робимо висновок, що нульові напруження можуть знаходиться лише у точках другого та четвертого квадрантів. Позначимо координати
Це рівняння є рівнянням прямої, що проходить крізь початок координат (центр ваги перерізу) і квадранти з різними знаками нормальних напружень. Така лінія називається нейтральною. Кутовий коефіцієнт цієї прямої:
Рисунок 3
Якщо зважити, що з формул (2)
то остаточно
Таким чином, нейтральна лінія завжди відхиляється від осі То ж у випадку косого або просторового згинання для перерізів ( Для визначення найбільш небезпечних точок (у розтягнутій та стислій зонах) у випадку довільного перерізу проведемо дві паралельні до нейтральної лінії прямі, які дотичні до контурних точок перерізу. У створі між цими прямими будується епюра сумарних нормальних напружень. Точки 1 та 2 є найбільш віддаленими від нейтральної лінії і тому найбільш напруженими (рис.3). У нашому прикладі в точці 1 діють максимальні розтягуючі, а у точці 2 – стискаючі напруження. Таким чином, умови міцності для перерізу мають вигляд:
де Якщо переріз має дві вісі симетрії, наприклад прямокутник, то співвідношення (9) дещо скорочуються:
В цих виразах
де У випадку, якщо матеріал стержня має однакову міцність на розтягання і стискання, тобто
Зрозуміло, що найбільші напруження будуть спостерігатись у найбільш небезпечних перерізах, де згинальні моменти набувають своїх максимальних значень. Відносно складових напруження Доречи, якщо переріз балки має виступаючі кути і може бути вписаний в прямокутник, то незалежно від положення нейтральної лінії найбільш віддаленими точками будуть відповідні кутові. У таких випадках, для розрахунків максимальних напружень у перерізі визначення положення нейтральної лінії втрачає сенс. Добір перерізів при косому та просторовому згинанні – задача більш складна, ніж при прямому плоскому згинанні. При її розв’язанні треба задатися відношенням моментів опору:
Тоді, з урахуванням (13), умова міцності (11) буде мати вигляд:
а моменти опору визначаються наступним чином:
У випадку просторового згинання, якщо згинальні моменти набувають максимальних значень у двох різних перерізах, задача вирішується за допомогою метода спроб з послідуючою перевіркою. Перша спроба виконується у перерізі, де діє максимальний за абсолютною величиною момент. У іншому (другому) перерізі обов’язково виконується перевірка.
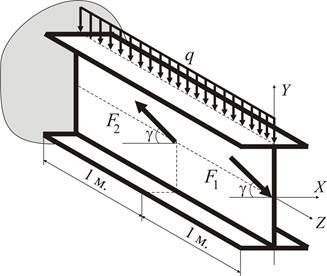
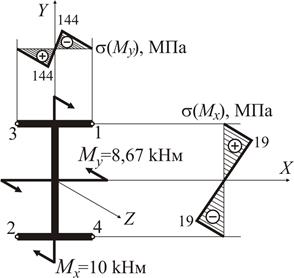
Приклад 1 Визначити номер двометрової консольної балки (рис. 4) з умови міцності, якщо
Рисунок 4
Двотаврова балка знаходиться в умовах складного (просторового) згинання, бо згідно зі схемою навантаження (рис. 4) можна визначити дві силові площини, які перетинають поздовжню вісь двотавру. Одна з цих площин співпадає з головною центральною площиною Розкладемо зусилля
У кожній площині збудуємо епюри згинальних моментів. Дією поперечних зусиль будемо нехтувати.
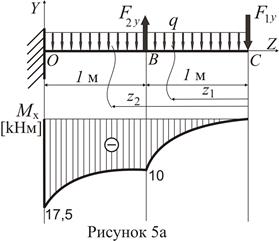
Найбільший за модулем згинальний момент
Рисунок 6
Зважаючи на правила знаків для згинальних моментів, можна констатувати, що у площині
Аналізуючи співвідношення
Для перерізу О теоретично необхідний момент опору дорівнює:
Для перерізу В теоретично необхідний момент опору дорівнює:
В якості моменту опору двотавру, що відповідає умові міцності в обох перерізах необхідно обирати більший з двох можливих:
З таблиць сортаменту добираємо найближчий більший двотавр №30а, який має наступні характеристики:
Тоді у перерізі В (рис. 7) максимальні напруження в точках 3,4 становлять:
Перенавантаження складає:
що цілком допустимо. Розподіл напружень в поперечному перерізі має вигляд:
Рисунок 7
Визначаючи переміщення Таким чином, повний прогин і кут повороту визначаються формулами:
Як приклад, обчислимо прогин вільного кінця консолі, навантаженою силою (рис.2а). Ці переміщення можна знайти багатьма способами (метод початкових параметрів, інтеграл Максвелла – Мора, спосіб Верещагіна і т.п.), які дають однакове рішення для прогину
Як і раніше розкладемо силу
відповідно у площині
Утворимо співвідношення
Порівнюючи його з (8), достаємо висновку:
Якщо зважити, що кути
Рисунок 8
тобто напрямок повного прогину у випадку косого та просторового згинання завжди ортогональний до нейтральної лінії перерізу. Тому для визначення цього напрямку необхідно попередньо знайти положення нейтральної лінії для будь-якого за формою перерізу.
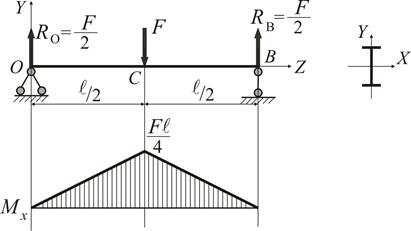
Приклад 2 Розглянемо двотаврову балку №70, завантажену силою посередині (рис. 9).
Рисунок 9
З таблиць сортаменту для двотаврів геометричні характеристики поперечного перерізу: Легко підрахувати опорні реакції, що становлять половину від сили (завдяки симетрії системи). Тоді при прямому згинанні
Максимальні напруження на полицях двотавру дорівнюють:
Максимальний прогин (у напрямку осі
Припустимо, що при монтажі балки була зроблена невелика похибка у
Рисунок 10
Розкладемо силу
Розрахункові схеми навантаження в площинах
а максимальні напруження при косому згинанні
Співвідношення
вказує на зростання напружень при косому згинанні більше ніж у півтори рази (на 51,4 %). Згідно з формулою (16) повний прогин
Рисунок 11
Підрахуємо спочатку кут нахилу нейтральної лінії. Згідно з (7)
Таким чином, напрямок повного прогину
Розрахунок свідчить, що у разі косого згинання прогини зростають майже вдвічі (на 99 %) для перерізів у яких Слід зауважити, що приведені результати мають місце для геометрично лінійної постановки задачі з малими переміщеннями, які розподіляються згідно з диференціальним рівнянням зігнутої осі балки [1]. Якщо прогини
|
||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 550; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.254.229 (0.011 с.) |

 вздовж осі стержня. Оскільки напруження
вздовж осі стержня. Оскільки напруження 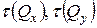 (а в окремих випадках і
(а в окремих випадках і 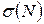 ), як правило малі, то для виявлення небезпечного перерізу у першу чергу використовують епюри згинальних та крутних моментів
), як правило малі, то для виявлення небезпечного перерізу у першу чергу використовують епюри згинальних та крутних моментів 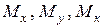 у співставленні з розташуванням перерізу стержня. Те ж свідчать і енергетичні методи опору матеріалів, бо у разі дії згинальних та (або) крутних моментів понад 98 % енергії поглинають саме ці деформації.
у співставленні з розташуванням перерізу стержня. Те ж свідчать і енергетичні методи опору матеріалів, бо у разі дії згинальних та (або) крутних моментів понад 98 % енергії поглинають саме ці деформації. . Спираючись на закони розподілу напружень від кожного силового фактору і використовуючи формули підрахунку сумарних (простий напружений стан) або еквівалентних напружень (у разі складного напруженого стану) визначають найбільш небезпечну точку перерізу.
. Спираючись на закони розподілу напружень від кожного силового фактору і використовуючи формули підрахунку сумарних (простий напружений стан) або еквівалентних напружень (у разі складного напруженого стану) визначають найбільш небезпечну точку перерізу.
 .
. , які й використовуються в умові міцності, сформульованій на базі відповідної гіпотези:
, які й використовуються в умові міцності, сформульованій на базі відповідної гіпотези:


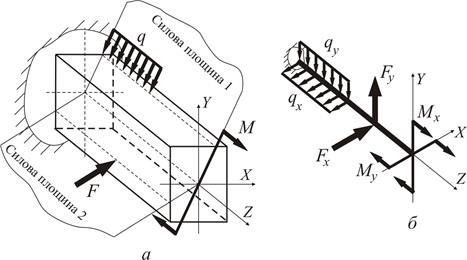
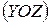 ,
, 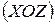 (рис. 1б). Таким чином, у будь-якому перерізі балки виникають чотири внутрішні силові фактори:
(рис. 1б). Таким чином, у будь-якому перерізі балки виникають чотири внутрішні силові фактори: 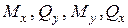 .
.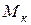 , що зумовлює вільне або стиснуте кручення.
, що зумовлює вільне або стиснуте кручення. .
.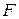 , яка лежить у силовій площині, нахиленій під кутом
, яка лежить у силовій площині, нахиленій під кутом 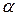 до головної площини
до головної площини 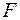 по головних осях перерізу і, таким чином, зведемо задачу косого згинання до комбінації двох плоских згинань у головних площинах
по головних осях перерізу і, таким чином, зведемо задачу косого згинання до комбінації двох плоских згинань у головних площинах 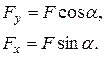 (1)
(1)
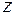 згинальні моменти визначаються за співвідношеннями:
згинальні моменти визначаються за співвідношеннями: (2)
(2) , при
, при 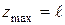 , який є найбільш небезпечним.
, який є найбільш небезпечним. (3)
(3)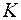 довільного перерізу, яка знаходиться у першому його квадранті (рис. 2б):
довільного перерізу, яка знаходиться у першому його квадранті (рис. 2б):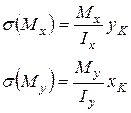 (4)
(4) (5)
(5) точки з напруженнями
точки з напруженнями  (рис. 3), тоді з формули (5) маємо:
(рис. 3), тоді з формули (5) маємо: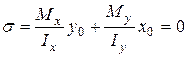 . (6)
. (6)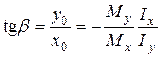 (7)
(7)
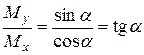 ,
,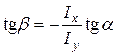 . (8)
. (8)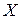 на кут
на кут 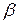 в ту ж сторону, в яку слід силової площини відхиляється від осі
в ту ж сторону, в яку слід силової площини відхиляється від осі 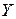 на кут
на кут  , а співвідношення
, а співвідношення 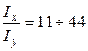 (що відповідає двотавру), легко підрахувати кут
(що відповідає двотавру), легко підрахувати кут  ) нейтральна лінія не є ортогональною до сліду площини
) нейтральна лінія не є ортогональною до сліду площини 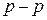 дії згинального моменту. Ця обставина є характерною рисою косого згинання. І навпаки, якщо головні моменти інерції однакові (
дії згинального моменту. Ця обставина є характерною рисою косого згинання. І навпаки, якщо головні моменти інерції однакові (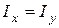 ), косе згинання унеможливлюється, бо кути
), косе згинання унеможливлюється, бо кути 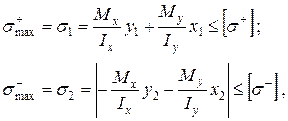 (9)
(9)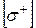 та
та  – допустимі напруження розтягання та стискання відповідно.
– допустимі напруження розтягання та стискання відповідно. (10)
(10) (11)
(11)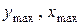 – координати найбільш віддалених від нейтральної лінії точок.
– координати найбільш віддалених від нейтральної лінії точок.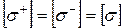 , то умови (10) перетворюються:
, то умови (10) перетворюються: (12)
(12)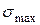 у виразах (10) та (12) можна зробити наступні спостереження. У перерізах, де
у виразах (10) та (12) можна зробити наступні спостереження. У перерізах, де 
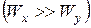 , що опиняються в умовах косого або просторового згинання, можна говорити про наявність «сильної»
, що опиняються в умовах косого або просторового згинання, можна говорити про наявність «сильної» 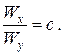 (13)
(13)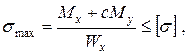 (14)
(14) (15)
(15) ,
,  ,
,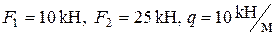 .
.
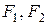 по головним осям перерізу, та зведемо складне згинання до двох плоских згинань в площинах
по головним осям перерізу, та зведемо складне згинання до двох плоских згинань в площинах 
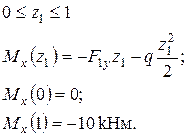


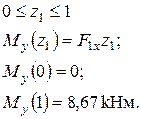

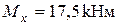 досягається в перерізі О, тому першу спробу добору двотавру зробимо саме для цього перерізу. Проаналізуємо напружений стан перерізу. З розподілу згинальних моментів у перерізі О визначимо знаки нормальних напружень у різних квадрантах перерізу (рис. 6).
досягається в перерізі О, тому першу спробу добору двотавру зробимо саме для цього перерізу. Проаналізуємо напружений стан перерізу. З розподілу згинальних моментів у перерізі О визначимо знаки нормальних напружень у різних квадрантах перерізу (рис. 6).
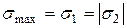 , то
, то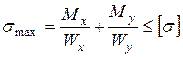
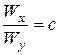 для двотаврів, можна дістати висновку, що середнє значення коефіцієнта
для двотаврів, можна дістати висновку, що середнє значення коефіцієнта  , тому
, тому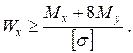
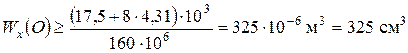 .
.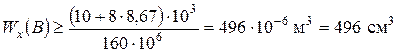 .
. .
.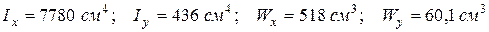 .
. .
.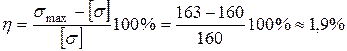 ,
,
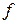 та кути повороту
та кути повороту 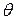 перерізів при косому та просторовому згинанні, також виходимо з принципу незалежності дії сил. Обчислюємо ці величини в кожній з головних площин
перерізів при косому та просторовому згинанні, також виходимо з принципу незалежності дії сил. Обчислюємо ці величини в кожній з головних площин 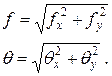 (16)
(16)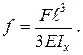 (17)
(17)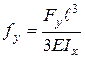 ,
,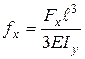 .
.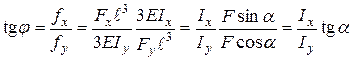 . (18)
. (18) .
. відлічуються від взаємно ортогональних напрямків (осей
відлічуються від взаємно ортогональних напрямків (осей 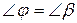 (рис. 8)
(рис. 8)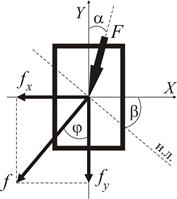


 .
. .
. ) посередині балки (переріз С) підраховується як [1]
) посередині балки (переріз С) підраховується як [1] .
. , на які стійка профілю відхилилася від вертикалі (рис. 10). Завдяки цьому маємо класичний випадок косого згинання.
, на які стійка профілю відхилилася від вертикалі (рис. 10). Завдяки цьому маємо класичний випадок косого згинання.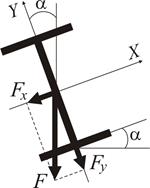
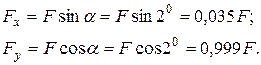
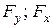 відповідно є подібними до схеми прямого згинання (рис. 9). Максимальні згинальні моменти у перерізі С дорівнюють:
відповідно є подібними до схеми прямого згинання (рис. 9). Максимальні згинальні моменти у перерізі С дорівнюють: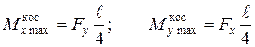


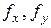 у головних площинах перерізу (рис. 11) Напрям повного прогину
у головних площинах перерізу (рис. 11) Напрям повного прогину  лежить на перпендикулярі до нейтральної лінії.
лежить на перпендикулярі до нейтральної лінії.
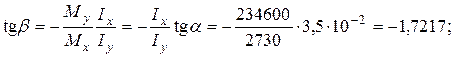
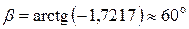
 . Підрахуємо повний прогин та порівняємо його з прогином при прямому згинанні.
. Підрахуємо повний прогин та порівняємо його з прогином при прямому згинанні.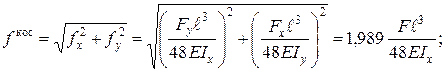

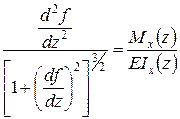 .
.


