
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мiнiстерство освiти і науки УкраїниСодержание книги
Поиск на нашем сайте
МIНIСТЕРСТВО ОСВIТИ І НАУКИ УКРАЇНИ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ „ХАРКIВСЬКИЙ ПОЛIТЕХНIЧНИЙ ІНСТИТУТ”
Киркач Б.М. Конохов В.І. Хавін В.Л. Шергін С.Ю.
„РОЗРАХУНКИ На міцність СТЕРЖНІВ при СКЛАДНОМУ деформуванні”
Навчально – методичний посібник з розділу курсу „Опір матеріалів” для студентів машинобудівних спеціальностей
ЗАТВЕРДЖЕНО редакційно – видавничою радою університету, протокол № 1 від 24 червня 2010 р.
Харків НТУ „ХПІ” 2010 ББК 30.121 Р64 УДК 620.17
Рецензенти: В.М. Кошельник д-р техн. наук, проф., Національний технічний університет „Харківський політехнічний інститут”, С.А. Вамболь канд. техн. наук, доцент, Університет цивільного захисту України
Автори: Киркач Б.М., Конохов В.І., Хавін В.Л., Шергін С.Ю.
Розрахунки на міцність стержнів при складному деформуванні. Навчально - методичний посібник з розділу курсу „Опір матеріалів” для студентів машинобудівних спеціальностей/ Киркач Б.М., Конохов В.І., Хавін В.Л., Шергін С.Ю. – Х.: НТУ “ХПІ”, 2010 –120 с.
ISBN Розглядаються теоретичні аспекти розрахунків при складному навантаженні, надаються приклади інженерних розрахунків на міцність стержнів при складному деформуванні; теоретичні основи напруженого стану в точці при комбінації різних видів простого деформування, надаються розрахункові схеми і чисельні дані для виконання індивідуальних розрахунково-проектувальних завдань, а також приклади їх розв’язання. Призначено для студентів машинобудівних спеціальностей. Може бути корисним для викладачів, а також для аспірантів, інженерів та наукових працівників. Іл. 80. Табл. 2. Бібліогр. 4 назв.
ББК 30.121
Вступ Сучасний етап науково-технічного розвитку потребує удосконалення методів розрахунку на міцність і жорсткість машинобудівних конструкцій з метою впровадження нових технологій, підвищення якості, надійності та довговічності машин, їх конкурентоспроможності на світовому ринку. Навчально-методичний посібник є складовою одиницею серії навчально-методичної літератури, підготовленої кафедрою опору матеріалів НТУ «ХПІ» для виконання індивідуальних розрахунково-проектувальних завдань студентами машинобудівних спеціальностей та модульного контролю засвоєного матеріалу. Посібник охоплює один з важливих розділів загального курсу опору матеріалів, а саме, розрахунки стержньових конструкцій в умовах їх складного деформування. Посібник призначений для засвоєння студентами загальних положень теорії та методики проведення розрахунків стержнів з урахуванням їх складного напруженого стану. У першому розділі посібника розглянуті основні види складної деформації стержнів, а саме: косе та просторове згинання, сумісна дія згинання та розтягання (стискання), загальні випадки дії сил на бруси круглого та прямокутного перерізу. Для кожного виду складної деформації надані приклади розв’язання задач, аналізу напруженого стану у точках небезпечного перерізу. У другому розділі надаються розрахункові схеми та числові дані для виконання індивідуальних розрахунково-проектувальних завдань, а також приклади їх розв’язання та оформлення. Для перевірки набутих теоретичних знань студентів з даної теми пропонуються контрольні запитання. Складне деформування стержнів Загальні положення Центральне розтягання – стискання ( Зустрічаються і більш складні випадки завантаження, коли у різних перерізах стержня одночасно діють різні комбінації компонент внутрішніх зусиль, складені з відомих видів простого деформування. Таку деформацію стержня, або його опір називають складним. У загальному випадку навантаження в поперечному перерізі бруса виникають усі шість внутрішніх зусиль - просторове (складне) згинання, або його окремий випадок – косе згинання, які мають місце при наявності згинальних моментів - згинання з розтяганням (стиканням), якщо у поперечних перерізах діють одночасно - сумісне згинання та кручення, обумовлене дією відповідних моментів У всіх зазначених видах складного деформування в перерізах бруса з’являються також і поперечні зусилля Якщо припустити, що деформації достатньо жорсткого стержня (бруса) малі й відповідають закону Гука, то до задач складного деформування можна застосувати принцип суперпозиції або принцип сумування дії сил. Згідно з цим принципом, результат від дії системи зусиль, що приводить загалом до складного деформування стержня, дорівнює сумі результатів, одержаних від кожної сили окремо, яка сама по собі утворює просту деформацію. Таким чином, напружений стан, що з’являється у стержні при складному завантаженні, можна здобути сумуванням напружених станів, спричинених окремими простими навантаженнями. Кожне з шістьох внутрішніх зусиль пов’язано з виникненням відповідних напружень. Поздовжня сила Тому напружений стан в окремій точці перерізу бруса при складному деформуванні може бути - простим, якщо діють лише нормальні - складним, коли спостерігається одночасна дія обох типів напружень. В обох випадках у довільній точці перерізу сумарні нормальні
Принцип суперпозиції може бути застосований також і для визначення деформованого стану стержня в умовах складного навантаження. Наприклад, прогини та кути поворотів перерізів стержня підраховуються у різних координатних площинах при простих навантаженнях, а їх результат поєднується у геометричну суму:
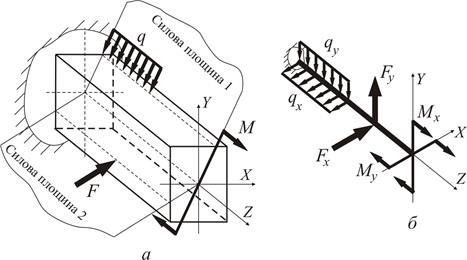
Просторове та косе згинання Згинання називають косим, якщо усі навантаження діють у одній (силовій) площині, яка перетинає вісь балки, але не включає жодної з головних центральних осей інерції перерізу. Якщо силових площин дві і більше, то таке згинання називається просторовим.
Рисунок 1
Розрахунки балок, які знаходяться в умовах косого або складного згинання, можна звести до сумісної дії двох плоских згинань у головних площинах. Для цього навантаження, що діють у довільних силових площинах треба спроектувати до головних площин Треба зазначити, що в даному методичному посібнику ми свідомо не торкаємося питань згинання тонкостінних відкритих профілів (з однією віссю симетрії або без неї), для яких поперечні сили, що проходять крізь центр ваги перерізу, породжують систему неврівноважених дотичних напружень. Останні утворюють крутний момент У практичних розрахунках на міцність для більшості перерізів малими дотичними напруженнями Незважаючи на загальні підходи до рішення задач косого і складного згинання, є деякі відмінності у цих випадках складного опору: а) при косому згинанні деформована вісь бруса є плоскою кривою, а при складному згинанні – просторовою; б) згинальні моменти Розглянемо жорстко затиснуту консольну балку, навантажену на вільному кінці силою Розкладемо зусилля
Рисунок 2
У довільному перерізі
Максимальні значення вони набувають у перерізі
Обчислимо напруження в точці
Оскільки тип напружень від дії згинальних моментів
Усі складові співвідношень (5) (згинальні моменти та координати) будемо вважати додатними, а знак приписувати кожному сполучнику окремо, зважаючи на деформації у відповідному квадранті. Аналізуючи розподіл нормальних напружень у перерізі (рис. 2б), робимо висновок, що нульові напруження можуть знаходиться лише у точках другого та четвертого квадрантів. Позначимо координати
Це рівняння є рівнянням прямої, що проходить крізь початок координат (центр ваги перерізу) і квадранти з різними знаками нормальних напружень. Така лінія називається нейтральною. Кутовий коефіцієнт цієї прямої:
Рисунок 3
Якщо зважити, що з формул (2)
то остаточно
Таким чином, нейтральна лінія завжди відхиляється від осі То ж у випадку косого або просторового згинання для перерізів ( Для визначення найбільш небезпечних точок (у розтягнутій та стислій зонах) у випадку довільного перерізу проведемо дві паралельні до нейтральної лінії прямі, які дотичні до контурних точок перерізу. У створі між цими прямими будується епюра сумарних нормальних напружень. Точки 1 та 2 є найбільш віддаленими від нейтральної лінії і тому найбільш напруженими (рис.3). У нашому прикладі в точці 1 діють максимальні розтягуючі, а у точці 2 – стискаючі напруження. Таким чином, умови міцності для перерізу мають вигляд:
де Якщо переріз має дві вісі симетрії, наприклад прямокутник, то співвідношення (9) дещо скорочуються:
В цих виразах
де У випадку, якщо матеріал стержня має однакову міцність на розтягання і стискання, тобто
Зрозуміло, що найбільші напруження будуть спостерігатись у найбільш небезпечних перерізах, де згинальні моменти набувають своїх максимальних значень. Відносно складових напруження Доречи, якщо переріз балки має виступаючі кути і може бути вписаний в прямокутник, то незалежно від положення нейтральної лінії найбільш віддаленими точками будуть відповідні кутові. У таких випадках, для розрахунків максимальних напружень у перерізі визначення положення нейтральної лінії втрачає сенс. Добір перерізів при косому та просторовому згинанні – задача більш складна, ніж при прямому плоскому згинанні. При її розв’язанні треба задатися відношенням моментів опору:
Тоді, з урахуванням (13), умова міцності (11) буде мати вигляд:
а моменти опору визначаються наступним чином:
У випадку просторового згинання, якщо згинальні моменти набувають максимальних значень у двох різних перерізах, задача вирішується за допомогою метода спроб з послідуючою перевіркою. Перша спроба виконується у перерізі, де діє максимальний за абсолютною величиною момент. У іншому (другому) перерізі обов’язково виконується перевірка.
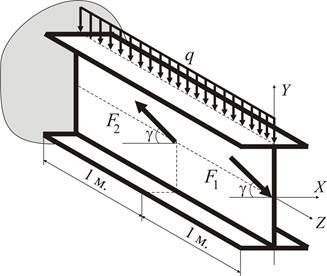
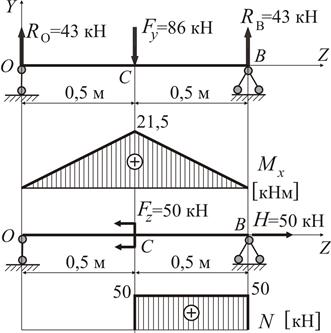
Приклад 1 Визначити номер двометрової консольної балки (рис. 4) з умови міцності, якщо
Рисунок 4
Двотаврова балка знаходиться в умовах складного (просторового) згинання, бо згідно зі схемою навантаження (рис. 4) можна визначити дві силові площини, які перетинають поздовжню вісь двотавру. Одна з цих площин співпадає з головною центральною площиною Розкладемо зусилля
У кожній площині збудуємо епюри згинальних моментів. Дією поперечних зусиль будемо нехтувати.
Найбільший за модулем згинальний момент
Рисунок 6
Зважаючи на правила знаків для згинальних моментів, можна констатувати, що у площині
Аналізуючи співвідношення
Для перерізу О теоретично необхідний момент опору дорівнює:
Для перерізу В теоретично необхідний момент опору дорівнює:
В якості моменту опору двотавру, що відповідає умові міцності в обох перерізах необхідно обирати більший з двох можливих:
З таблиць сортаменту добираємо найближчий більший двотавр №30а, який має наступні характеристики:
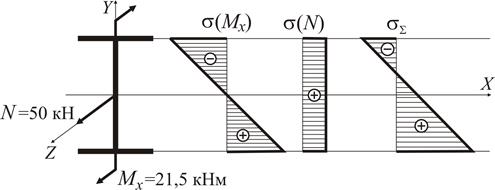
Тоді у перерізі В (рис. 7) максимальні напруження в точках 3,4 становлять:
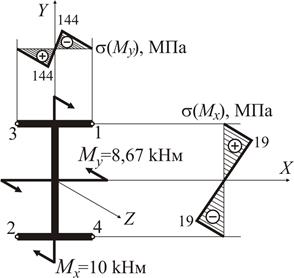
Перенавантаження складає:
що цілком допустимо. Розподіл напружень в поперечному перерізі має вигляд:
Рисунок 7
Визначаючи переміщення Таким чином, повний прогин і кут повороту визначаються формулами:
Як приклад, обчислимо прогин вільного кінця консолі, навантаженою силою (рис.2а). Ці переміщення можна знайти багатьма способами (метод початкових параметрів, інтеграл Максвелла – Мора, спосіб Верещагіна і т.п.), які дають однакове рішення для прогину
Як і раніше розкладемо силу
відповідно у площині
Утворимо співвідношення
Порівнюючи його з (8), достаємо висновку:
Якщо зважити, що кути
Рисунок 8
тобто напрямок повного прогину у випадку косого та просторового згинання завжди ортогональний до нейтральної лінії перерізу. Тому для визначення цього напрямку необхідно попередньо знайти положення нейтральної лінії для будь-якого за формою перерізу.
Приклад 2 Розглянемо двотаврову балку №70, завантажену силою посередині (рис. 9).
Рисунок 9
З таблиць сортаменту для двотаврів геометричні характеристики поперечного перерізу: Легко підрахувати опорні реакції, що становлять половину від сили (завдяки симетрії системи). Тоді при прямому згинанні
Максимальні напруження на полицях двотавру дорівнюють:
Максимальний прогин (у напрямку осі
Припустимо, що при монтажі балки була зроблена невелика похибка у
Рисунок 10
Розкладемо силу
Розрахункові схеми навантаження в площинах
а максимальні напруження при косому згинанні
Співвідношення
вказує на зростання напружень при косому згинанні більше ніж у півтори рази (на 51,4 %). Згідно з формулою (16) повний прогин
Рисунок 11
Підрахуємо спочатку кут нахилу нейтральної лінії. Згідно з (7)
Таким чином, напрямок повного прогину
Розрахунок свідчить, що у разі косого згинання прогини зростають майже вдвічі (на 99 %) для перерізів у яких Слід зауважити, що приведені результати мають місце для геометрично лінійної постановки задачі з малими переміщеннями, які розподіляються згідно з диференціальним рівнянням зігнутої осі балки [1]. Якщо прогини
Приклад 3 Доберемо номер двотаврової стійки, нахиленої до горизонту під кутом
Рисунок 15
Будемо вважати, що навантаження здійснюється в площині Проектуючи силу
Рисунок 16
Аналіз епюр згинального моменту
Рисунок 17
Із сортаменту для двотаврів знаходимо найближчий більший за моментом опору. Це двотавр № 18, який має Перевіримо добір з урахуванням напружень розтягання від поздовжньої сили
Перенапруження для даного двотавра становить 7,3 % >5 %. Тому треба збільшити номер двотавра і призначити наступний – 18а, для якого У цьому разі
Приклад 4 Як приклад розрахунків на позацентрове розтягання (стискання), доберемо допустиме значення сили
Рисунок 21
Для проведення розрахунків на позацентрове розтягання (стискання) першочергово необхідно визначити геометричні характеристики поперечного перерізу відносно головних центральних осей інерції (осьові моменті інерціїї, радіуси інерції, площу перерізу). Спочатку для складного перерізу бруса визначаємо положення центру ваги. Для цього складний профіль переріза розіб’ємо на два прямокутника з власними центральними осями Залишається визначити розташування центру ваги вздовж осі
де
Рисунок 22
Для застосування формули (33) треба обрати опорну вісь
Отриманий результат відкладаємо від опорної осі Сумарна площа перерізу визначається як алгебраїчна сума площ окремих частин:
Осьові моменти інерції перерізу відносно головних центральних осей інерції визначаються за виразами [1]:
де
У системі головних центральних осей інерції полюс (точка, де прикладена сила Наступним кроком до вирішення задачі має бути приведення сили
Рисунок 23
Таким чином маємо:
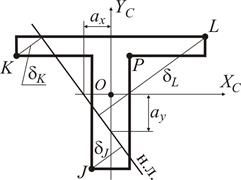
Силові фактори (35) діють у будь-якому перерізі колони і призводять до появи нормальних напружень, розподіл яких приведено на рис. 23. З цього розподілу витікає, що точки першого квадранту (де розташований полюс) мають напруження одного знаку (від’ємні). То ж нейтральна лінія має пройти крізь другий, третій та четвертий квадранти (рис. 24).
Рисунок 24.
Згідно (30) підрахуємо відрізки
Таким чином, рівняння нейтральної лінії згідно з (29) стає:
або після алгебраїчних перетворень доведемо його до стандартного виду
Нейтральна лінія розподіляє переріз на дві зони. У зоні стискаючих напружень найбільш віддаленою є кутова точка
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 365; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.12.41 (0.009 с.) |

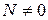 ), кручення (
), кручення ( ), зсув (
), зсув ( або
або 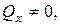 ), плоске поперечне згинання (
), плоске поперечне згинання (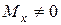 ;
; 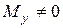 ;
; 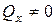 ) є так званими простими видами деформування стержнів. Характерною рисою простого деформування є наявність одного або двох внутрішніх силових факторів у довільному перерізі стержня (балки, бруса).
) є так званими простими видами деформування стержнів. Характерною рисою простого деформування є наявність одного або двох внутрішніх силових факторів у довільному перерізі стержня (балки, бруса).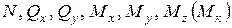 . На практиці одночасна дія всіх силових факторів спостерігається не часто. Найбільш поширеними видами складного деформування є наступні:
. На практиці одночасна дія всіх силових факторів спостерігається не часто. Найбільш поширеними видами складного деформування є наступні: ;
; ;
;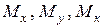 ;
; .
.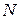 і згинальні моменти
і згинальні моменти 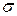 , крутний момент
, крутний момент 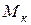 та поперечні сили
та поперечні сили 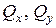 дають дотичні напруження
дають дотичні напруження 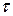 .
.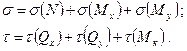
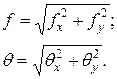
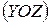 ,
, 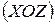 (рис. 1б). Таким чином, у будь-якому перерізі балки виникають чотири внутрішні силові фактори:
(рис. 1б). Таким чином, у будь-якому перерізі балки виникають чотири внутрішні силові фактори: 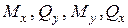 .
.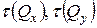 , як правило нехтують. Таким чином, врахують лише нормальні напруження від дії згинальних моментів
, як правило нехтують. Таким чином, врахують лише нормальні напруження від дії згинальних моментів 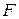 , яка лежить у силовій площині, нахиленій під кутом
, яка лежить у силовій площині, нахиленій під кутом 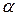 до головної площини
до головної площини 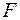 по головних осях перерізу і, таким чином, зведемо задачу косого згинання до комбінації двох плоских згинань у головних площинах
по головних осях перерізу і, таким чином, зведемо задачу косого згинання до комбінації двох плоских згинань у головних площинах 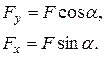 (1)
(1)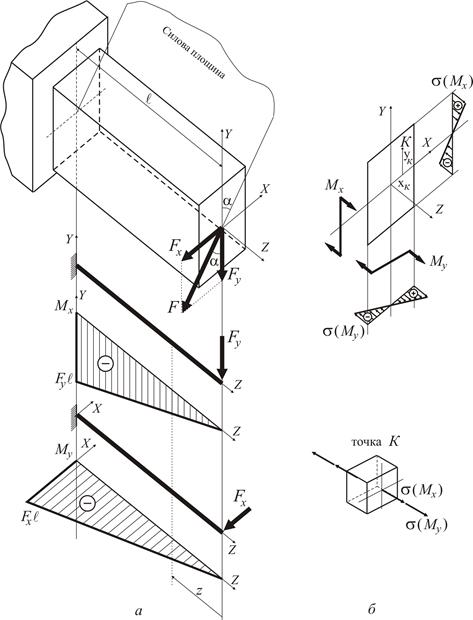
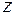 згинальні моменти визначаються за співвідношеннями:
згинальні моменти визначаються за співвідношеннями: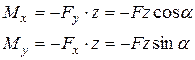 (2)
(2) , при
, при 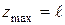 , який є найбільш небезпечним.
, який є найбільш небезпечним. (3)
(3)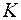 довільного перерізу, яка знаходиться у першому його квадранті (рис. 2б):
довільного перерізу, яка знаходиться у першому його квадранті (рис. 2б):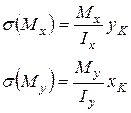 (4)
(4) (5)
(5)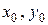 точки з напруженнями
точки з напруженнями 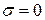 (рис. 3), тоді з формули (5) маємо:
(рис. 3), тоді з формули (5) маємо: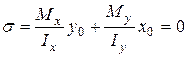 . (6)
. (6)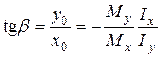 (7)
(7)
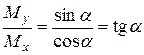 ,
,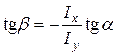 . (8)
. (8)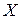 на кут
на кут 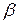 в ту ж сторону, в яку слід силової площини відхиляється від осі
в ту ж сторону, в яку слід силової площини відхиляється від осі 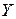 на кут
на кут  , а співвідношення
, а співвідношення 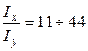 (що відповідає двотавру), легко підрахувати кут
(що відповідає двотавру), легко підрахувати кут  ) нейтральна лінія не є ортогональною до сліду площини
) нейтральна лінія не є ортогональною до сліду площини 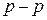 дії згинального моменту. Ця обставина є характерною рисою косого згинання. І навпаки, якщо головні моменти інерції однакові (
дії згинального моменту. Ця обставина є характерною рисою косого згинання. І навпаки, якщо головні моменти інерції однакові (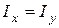 ), косе згинання унеможливлюється, бо кути
), косе згинання унеможливлюється, бо кути 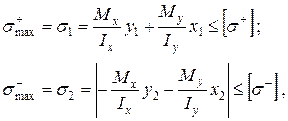 (9)
(9)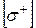 та
та  – допустимі напруження розтягання та стискання відповідно.
– допустимі напруження розтягання та стискання відповідно. (10)
(10) (11)
(11)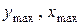 – координати найбільш віддалених від нейтральної лінії точок.
– координати найбільш віддалених від нейтральної лінії точок.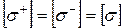 , то умови (10) перетворюються:
, то умови (10) перетворюються: (12)
(12)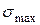 у виразах (10) та (12) можна зробити наступні спостереження. У перерізах, де
у виразах (10) та (12) можна зробити наступні спостереження. У перерізах, де 
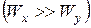 , що опиняються в умовах косого або просторового згинання, можна говорити про наявність «сильної»
, що опиняються в умовах косого або просторового згинання, можна говорити про наявність «сильної» 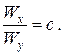 (13)
(13)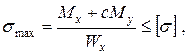 (14)
(14) (15)
(15) ,
, 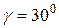 ,
,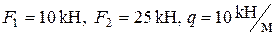 .
.
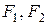 по головним осям перерізу, та зведемо складне згинання до двох плоских згинань в площинах
по головним осям перерізу, та зведемо складне згинання до двох плоских згинань в площинах 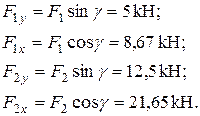
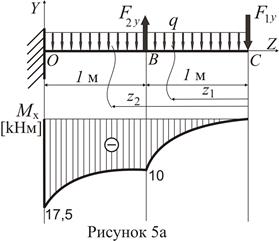
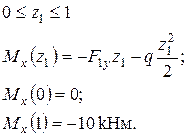


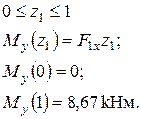

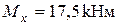 досягається в перерізі О, тому першу спробу добору двотавру зробимо саме для цього перерізу. Проаналізуємо напружений стан перерізу. З розподілу згинальних моментів у перерізі О визначимо знаки нормальних напружень у різних квадрантах перерізу (рис. 6).
досягається в перерізі О, тому першу спробу добору двотавру зробимо саме для цього перерізу. Проаналізуємо напружений стан перерізу. З розподілу згинальних моментів у перерізі О визначимо знаки нормальних напружень у різних квадрантах перерізу (рис. 6).
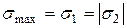 , то
, то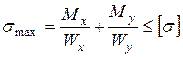
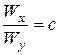 для двотаврів, можна дістати висновку, що середнє значення коефіцієнта
для двотаврів, можна дістати висновку, що середнє значення коефіцієнта  , тому
, тому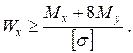
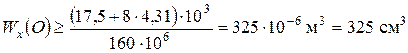 .
.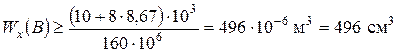 .
. .
.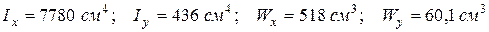 .
. .
.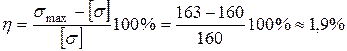 ,
,
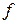 та кути повороту
та кути повороту 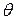 перерізів при косому та просторовому згинанні, також виходимо з принципу незалежності дії сил. Обчислюємо ці величини в кожній з головних площин
перерізів при косому та просторовому згинанні, також виходимо з принципу незалежності дії сил. Обчислюємо ці величини в кожній з головних площин 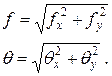 (16)
(16)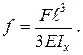 (17)
(17)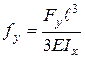 ,
,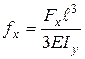 .
.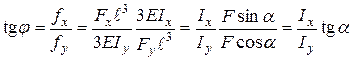 . (18)
. (18) .
. відлічуються від взаємно ортогональних напрямків (осей
відлічуються від взаємно ортогональних напрямків (осей 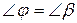 (рис. 8)
(рис. 8)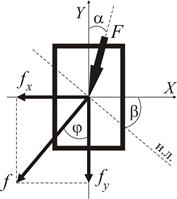


 .
. .
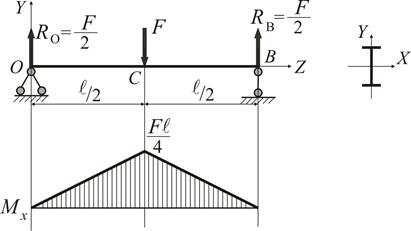
. ) посередині балки (переріз С) підраховується як [1]
) посередині балки (переріз С) підраховується як [1] .
. , на які стійка профілю відхилилася від вертикалі (рис. 10). Завдяки цьому маємо класичний випадок косого згинання.
, на які стійка профілю відхилилася від вертикалі (рис. 10). Завдяки цьому маємо класичний випадок косого згинання.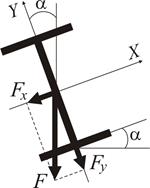
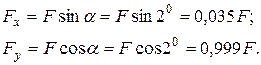
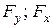 відповідно є подібними до схеми прямого згинання (рис. 9). Максимальні згинальні моменти у перерізі С дорівнюють:
відповідно є подібними до схеми прямого згинання (рис. 9). Максимальні згинальні моменти у перерізі С дорівнюють: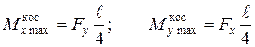


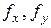 у головних площинах перерізу (рис. 11) Напрям повного прогину
у головних площинах перерізу (рис. 11) Напрям повного прогину  лежить на перпендикулярі до нейтральної лінії.
лежить на перпендикулярі до нейтральної лінії.
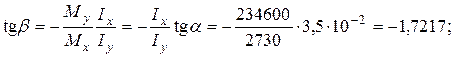
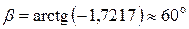
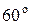 . Підрахуємо повний прогин та порівняємо його з прогином при прямому згинанні.
. Підрахуємо повний прогин та порівняємо його з прогином при прямому згинанні.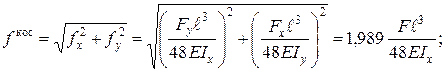

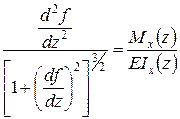 .
.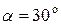 під дією сили
під дією сили  (рис. 15а). Нехай допустимі напруження для сталі становлять
(рис. 15а). Нехай допустимі напруження для сталі становлять 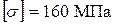 .
.
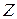 (рис. 15б), маємо сумісну дію плоского прямого поперечного згинання в площині
(рис. 15б), маємо сумісну дію плоского прямого поперечного згинання в площині 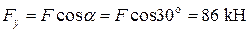 та розтягання балки у перерізах ділянки ВС від сили
та розтягання балки у перерізах ділянки ВС від сили 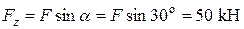 .
.
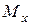 та поздовжньої сили
та поздовжньої сили 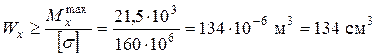
 .
.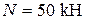 .
.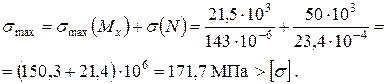
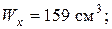
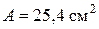 .
.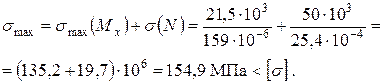
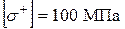 ,
, 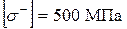 . Розміри перерізу колони наведені на рис. 21.
. Розміри перерізу колони наведені на рис. 21.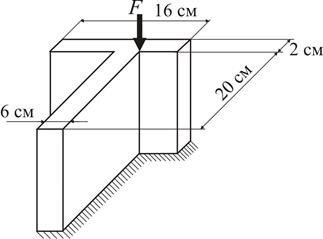
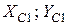 та
та 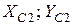 відповідно (рис. 22). Збіг центральних осей
відповідно (рис. 22). Збіг центральних осей  .
. (33)
(33)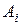 – площа кожної складової перерізу,
– площа кожної складової перерізу,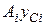 – статичний момент площі, відносно осі
– статичний момент площі, відносно осі  – координата центра ваги складової площі перерізу.
– координата центра ваги складової площі перерізу.
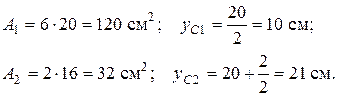
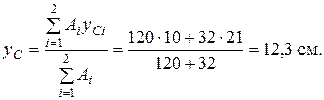
 .
.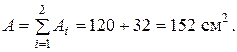
 (34)
(34)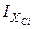 ,
, 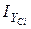 – моменти інерції складової перерізу, підраховані відносно власних центральних осей;
– моменти інерції складової перерізу, підраховані відносно власних центральних осей;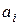 – відстань між осями
– відстань між осями 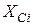 та
та 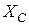 ;
;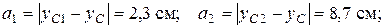
 – відстань між осями
– відстань між осями 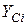 та
та 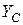 . Для перерізу з віссю симетрії
. Для перерізу з віссю симетрії  ,
, 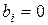
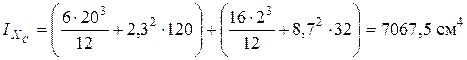 ;
;


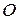 . На рис. 23 в цій точці з’являється окрім сили
. На рис. 23 в цій точці з’являється окрім сили 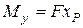 у площині
у площині 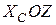 та
та 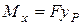 у площині
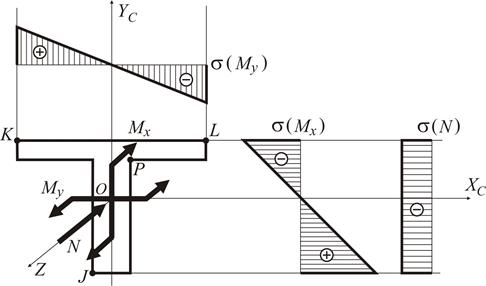
у площині 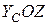 .
.
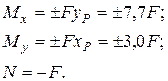 (35)
(35)
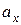 та
та 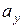 :
: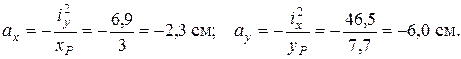

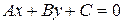 :
: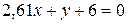 . (36)
. (36) (рис. 24). Найбільш віддаленою точкою у зоні розтягуюч
(рис. 24). Найбільш віддаленою точкою у зоні розтягуюч 


