Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сумісна дія просторового згинання з розтяганням (стисканням)Содержание книги
Поиск на нашем сайте
Для отримання цього виду складного деформування стержня дещо ускладнімо розрахункову схему косого або просторового згинання, додавши до неї осьове навантаження силою Розклавши, як і раніше, зусилля
у довільному перерізі
Рисунок 12
Рисунок 13
Малими дотичними напруженнями від дії поперечних зусиль Внутрішні зусилля перерізу (рис.13б) приводять до появи нормальних напружень, розподіл яких наведено на рис. 14.
Рисунок 14
Таким чином, у довільній точці перерізу маємо простий (лінійний) напружений стан.
Як і у рівняннях (5), знаки приписуємо кожному сполучнику формули (19) окремо, залежно від деформації відповідного квадранту переріза. Умови міцності для цього виду деформованого стану можна сформулювати наступним чином: а) якщо матеріал стержня має різну міцність на розтягання – стискання:
де б) у разі однакового опору розтяганню (стисканню), тобто коли
в) для перерізу, що має дві осі симетрії
а у разі, якщо
д) для перерізу, що має форму кола або кільця, завдяки співвідношенням
вирази умови міцності набувають вигляду:
а при
При сумісній дії розтягання (стискання) та складного або косого згинання нейтральна лінія є також прямою, але такою, що не перетинає центр ваги перерізу (початок координат) завдяки наявності
Шляхом алгебраїчних перетворень зведемо (22) до рівняння прямої у «відрізках на координатних осях»
Таким чином, у даному випадку складного опору нейтральна лінія є прямою, яка проходить крізь квадранти з різними знаками нормальних напружень і відсікає відрізки:
на відповідних координатних осях. Добір розмірів перерізу при сумісній дії згинання та розтягання (стискання) проводиться спочатку без впливу поздовжньої сили
Для бруса прямокутного або двотаврового перерізу
Співвідношенням Одержані співвідношення (19) – (26) легко поширюються на окремий випадок сумісної дії плоского згинання та розтягання (стискання). Для цього в зазначених рівняннях треба прийняти
Приклад 3 Доберемо номер двотаврової стійки, нахиленої до горизонту під кутом
Рисунок 15
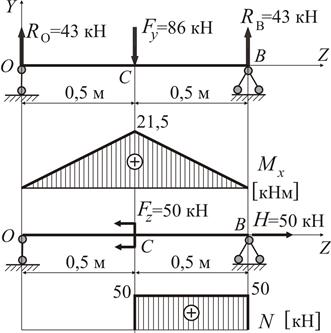
Будемо вважати, що навантаження здійснюється в площині Проектуючи силу
Рисунок 16
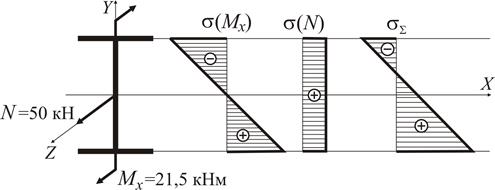
Аналіз епюр згинального моменту
Рисунок 17
Із сортаменту для двотаврів знаходимо найближчий більший за моментом опору. Це двотавр № 18, який має Перевіримо добір з урахуванням напружень розтягання від поздовжньої сили
Перенапруження для даного двотавра становить 7,3 % >5 %. Тому треба збільшити номер двотавра і призначити наступний – 18а, для якого У цьому разі
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 372; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.133.214 (0.006 с.) |

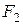 (рис. 12).
(рис. 12).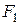 по головних осях X та Y
по головних осях X та Y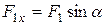 ;
; 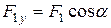
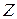 балки маємо дію двох згинальних моментів
балки маємо дію двох згинальних моментів 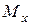 ,
, 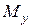 та поздовжньої сили
та поздовжньої сили 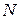 (рис.13а). Напрямок їх дії показаний на рис. 13б.
(рис.13а). Напрямок їх дії показаний на рис. 13б.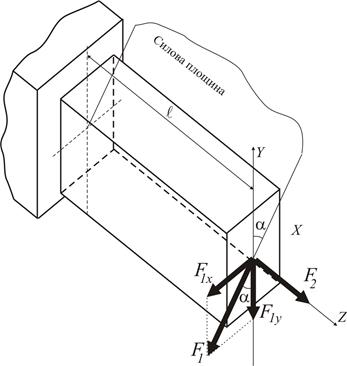
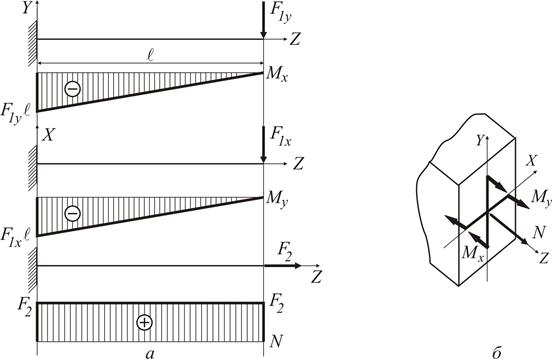
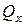 ,
, 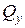 (як і у випадку косого або просторового згинання) будемо нехтувати.
(як і у випадку косого або просторового згинання) будемо нехтувати.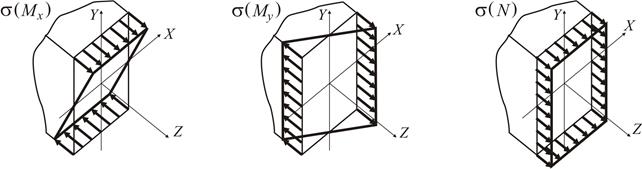
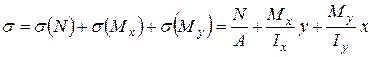 . (19)
. (19)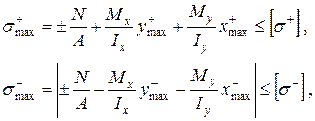 (20)
(20)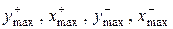 – координати найбільш віддалених від нейтральної лінії точок у розтягнутій та стислій зоні відповідно.
– координати найбільш віддалених від нейтральної лінії точок у розтягнутій та стислій зоні відповідно.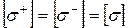
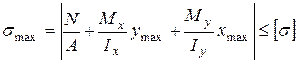 ; (21)
; (21)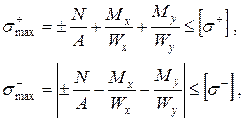 (20.1)
(20.1)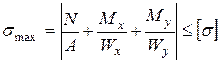 (21.1)
(21.1)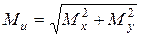 ;
; 
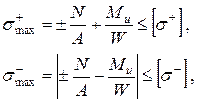 (20.2)
(20.2)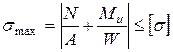 . (21.2)
. (21.2)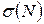 (рис. 14). Неважко це встановити і математично, якщо вважати
(рис. 14). Неважко це встановити і математично, якщо вважати 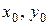 координатами точки, яка належить до нейтральної лінії. Тоді з (19) витікає рівняння цієї прямої:
координатами точки, яка належить до нейтральної лінії. Тоді з (19) витікає рівняння цієї прямої: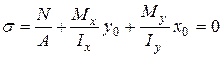 . (22)
. (22)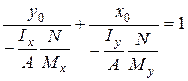 . (23)
. (23)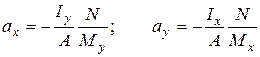 (24)
(24)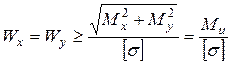 . (25)
. (25)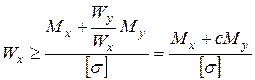 . (26)
. (26)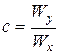 треба задатися. Так, для прямокутного перерізу
треба задатися. Так, для прямокутного перерізу 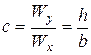 , для двотаврової балки приймають середнє відношення
, для двотаврової балки приймають середнє відношення 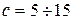 і знаходять потрібний номер двотавра методом послідовних наближень. Першу спробу роблять по найбільшому за модулем згинальному моменту. Друга спроба, у випадку складного згинання, повинна перевірятися з урахуванням іншої складової згинального моменту та додаткових напружень від поздовжньої сили
і знаходять потрібний номер двотавра методом послідовних наближень. Першу спробу роблять по найбільшому за модулем згинальному моменту. Друга спроба, у випадку складного згинання, повинна перевірятися з урахуванням іншої складової згинального моменту та додаткових напружень від поздовжньої сили 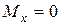 (або
(або 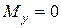 ).
).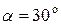 під дією сили
під дією сили  (рис. 15а). Нехай допустимі напруження для сталі становлять
(рис. 15а). Нехай допустимі напруження для сталі становлять 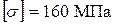 .
.
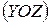 , яка є головною площиною балки.
, яка є головною площиною балки.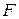 на головні осі
на головні осі 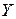 та
та 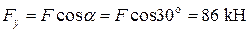 та розтягання балки у перерізах ділянки ВС від сили
та розтягання балки у перерізах ділянки ВС від сили 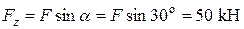 .
.
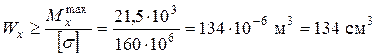
 .
.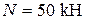 .
.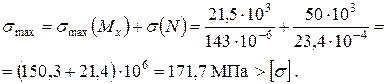
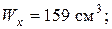
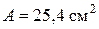 .
.