Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ряды распределения: значение и видыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ряды распределения получают в результате группировки единиц совокупности по какому-либо варьирующему признаку, поэтому они часто используются для характеристики структуры изучаемых явлений. Например, распределение работников по формам оплаты труда, как в числовом выражении, так и в %. Всякий ряд распределения состоит из двух частей: значений варьирующего признака и соответствующих им численности единиц рассматриваемой совокупности. Численности единиц с одинаковым значением признака называются частотами, а их сумма (итог) – объемом ряда. Частоты, выраженные в долях единицы или % к итогу называются частостями. Ряды распределения могут быть образованы по атрибутивному или количественному признаку. В связи с этим они подразделяются на: атрибутивные, вариационные. Вариационные делятся на: - дискретные (ряды, в которых значение признаков, положенных в основу их образования, выражены в виде вполне определенных величин (обычно целых чисел)). - интервальные (в которых значения, положенные в основу образования признаков выражены в определенных пределах, интервалах, т.е. для каждой выделяемой группы указаны мин. и макс. границы признаков). Интервальные: - закрытые - открытые Интервалы, у которых показана только верхняя или нижняя граница – открытые, а если обе – закрытые. 12. Графически вариационные ряды могут быть представлены в виде: - полигона - гистограммы - куммулятивной кривой Полигон – график, изображающий вариационный ряд с помощью замкнутого многоугольника. Для его построения на оси Х откладывают значение признака, а соответствующие им частоты или частости – на У, или наоборот. Точки с координатами соединяются между собой, а из крайних точек опускается перпендикуляр на ось Х. Гистограмма – график, изображающий интервальный вариационный ряд в виде прилегающих друг к другу прямоугольников. Для построения: на оси Х откладываются отрезки, соответствующие величинам интервалов, высота отрезков соответствует частотам или частостям, т.о. каждому интервалу соответствует свой прямоугольник. Кумулятивная кривая – график, изображающей вариационный ряд по данным о последовательно суммированных, т.е. накопленных частотах или частостях.
14.15 Абсолютные и относительные величины: сущность, значение, формы выражения и виды. Выражают абсолютные величины в натуральных, трудовых и стоимостных единицах. Натуральные единицы характеризуют явление в свойственной им натурально-вещественной форме и выражаются в единицах длины, объема, массы и т.д. Для выражения величины сложных явлений употребляется комбинированные натуральные величины т/км, пас/км или условно-натуральные (приведенная работа дороги). К трудовым единицам измерения относ человеко-час, человеко-день, нормо-час и тд. Стоимостные единицы измеряются в руб, евро, доллар. Относительными в статистике называются величины, характеризующие развитие общественных явлений во времени и пространстве, их структуру, а также количественное соотношение признаков явлений. Всякая относительная величина есть результат сопоставления между собой двух других величин (абсолютных, средних или относительных). По способу расчета это дробь, при этом числитель – сравниваемая величина, знаменатель – база относительного сравнения. Выражаются относительные величины в коэффициентах, процентах, промилле, продецимилле, или в единицах, присущих относимым абсолютным величинам. Относительные величины подразделяются на несколько видов: - относительная величина планового задания - относительная величина выполнения плана - относительная величина динамики - относительная величина структуры - относительная величина пространственного сравнения - относительная величина координации - относительная величина интенсивности Относительные величины пространственного сравнения отражают результат сравнения одноименных показателей, относящихся к различным объектам за один и тот же период.
16. Сущность статистических средних величин и правила их применения. Метод средних это особая форма статистического обобщения. Применение этого метода возможно только при наличии вариации признака у совокупности однородных явлений. Средние величины могут быть как абсолютными, так и относительными (средняя зарплата, средний % выполнения плана). Средняя величина характеризует однородные по своему содержанию совокупности (типичная средняя). Для обеспечения объективности и типичности средних необходимо выполнение двух условий: 1) совокупность должна быть качественно однородная. 2) должны быть использованы не единичные, а массовые данные только в этом случае взаимопогашаются возможные случайные отклонения. В статистике применяются следующие виды средних:: - средняя арифметическая - средняя гармоническая - средняя квадратическая - средняя геометрическая - средняя хронологическая Эти средние относят к классу степенных средних. Кроме них используются структурные средние – мода и медиана.
Средняя арифметическая: - простая
- взвешенная
а n – количество единиц совокупности
Средняя гармоническая: Представляет собой обратную среднюю арифметическую из обратных величин
Средняя квадратическая Используется в том случае, когда необходимо возводить варианты в квадрат
Средняя геометрическая
Средняя хронологическая
А Взвешенная применяется в тех случаях, когда интервалы между явлениями неравны
Для обобщенной количественной характеристики общественных явлений используют описательные или структурные средние – мода и медиана. Мода – наиболее часто встречающееся значение признаков совокупности. Медиана - численное значение признака, расположенное в середине ранжированного ряда,. Которое делит этот ряд на 2 равные по численности части. Для определения медианы вначале находят её место в ряду по формуле
Если число единиц четное, то место медианы в ряду определяется по формуле
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 918; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.01 с.) |


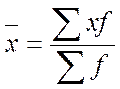 , где f – частота повторений соответствующего признака (веса) – х,
, где f – частота повторений соответствующего признака (веса) – х, - простая,
- простая,  - взвешенная, w – размер признака
- взвешенная, w – размер признака - простая,
- простая,  - взвешенная
- взвешенная
 n – количество единиц наблюдений
n – количество единиц наблюдений
 , где n – число членов ряда.
, где n – число членов ряда.