Контроль за соревновательной деятельностью.

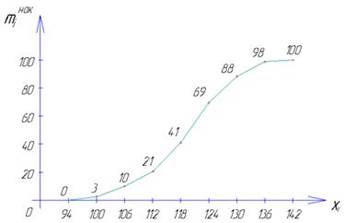
Соревновательная деятельность представляет собой организованное по определённым правилам соперничество с целью выявления и объективного сравнения спортивного мастерства. Основные направления обследования соревновательной деятельности: 1) определение общего числа и результативности технико-тактических действий; 2) определение эффективности и устойчивости спортивной техники; 3) контроль за спортивной тактикой; 4) измерение физиологических и биохимических реакций организма в условиях соревнований и непосредственно после их завершения; 5) контроль за психическим состоянием. Способы регистрации соревновательной деятельности: запись на видео, проговаривание на диктофон, стенографирование, запись действий спортсмена до старта, во время выполнения действий и по окончании выполнения действий.

25. Предмет спортивной метрологии. СМ – это наука об измерениях в ФВиС. Это приложение общей метрологии, основной задачей которой является обеспечение точности и единства измерений. Общая метрология – это физическая величина. СМ включает педагогические, психологические, социальные, биологические показатели. Предметом СМ является комплексный контроль в ФВиС и использование иго результатов в планировании подготовки спортсменов. Комплексный контроль включает в себя не только физические показатели, но и педагогические, психологические, социологические и другие показатели. Виды контроля: этапный, текущий и оперативный.

26. Разновидность норм. Нормой в СМ называется граничная величина результата теста, на основе которой производится классификация спортсменов. Есть официальные и неофициальные нормы. Виды норм: 1)сопоставительные нормы (устанавливаются после достижений людей, принадлежащих к одной и той же совокупности); 2)индивидуальные нормы (основаны на сравнении показателей одного и того же спортсмена в разных состояниях, Имеют значение для индивидуализации тренировки); 3) должные нормы (устанавливаются на основании требований, которые предъявляют человеку условия жизни, профессия и т.д.). Существуют возрастные нормы, а так же возрастные нормы с учётом биологического возраста и особенностей телосложения.

27. Понятия теории оценок. Исключительно редко для оценки подготовленности спортсмена используют 1 тест. Как правило, комплексный контроль использует нескольких тестов. Один тест с помощью специальных методов не оценивается. Когда тестов много и в различных единицах, то сравнение их не возможно. Решить эту проблему можно представив результаты в виде оценок. Оцениванием называется унифицированная мера успеха, в каком либо задании, в тесте. Процесс состоит из стадий: 1) подбирается шкала с помощью, которой возможен перевод результата теста в оценки; 2) в соответствии с выбранной шкалой результаты теста переводятся в очки, баллы; 3) полученные очки сравниваются с нормами, и выводится итоговая оценка, которая характеризует уровень подготовленности спортсмена относительного других спортсменов. Основные задачи: 1) на основании результатов тестов сопоставить различные достижения в соревновательных упр., т.е. научно обоснованные разрядные нормы в разных видах спорта; 2) это позволяет достичь равенства в них разрядных норм; 3) классификация тестов по результатам конкретного спортсмена; 4) следует установить структуру тренированности каждого из спортсменов, подвергшихся тестированию. Простейший способ тестирования – ранжирование. Для перевода результатов оценки применяют специальные шкалы. Пропорциональная шкала, прогрессивная и регрессивная шкала, сигмовидная – теоретические виды шкал. Практические – стандартная, перцинтильлная, шкала ГЦОЛИВКа. Также проводится оценка комплекса тестов. 3-и способа: с помощью экспертной оценки по коэффициенту; на основании факторного анализа; коэффициентом корреляции между тестом и достижением в соревновании.

28. Содержание и организация этапного контроля. Цель этапного контроля – получить информацию, на основании которой можно составить планы подготовки на период, этап или какой-то другой относительно длительный срок. Программа этапного контроля: 1-й блок- составляют общие для многих видов спорта не специфические тесты; Критериями физической работоспособности в таких тестах являются: 1) время, в течение которого спортсмен мог выполнять задание; 2) объем работы (он определяется как произведение средней мощности на время теста); 3) максимальное потребление кислорода. 2-й блок – это специфические тесты, структура которых должна соответствовать структуре соревновательного упражнения. Мера их информативности определяется по величине коэффициентов корреляции между результатами в соревнованиях и достижениями в тестах. По возможности применяются тренажеры. При организации этапного контроля следует на всех этапах подготовки использовать одни и те же тесты, для получения динамики показателей и проанализировать её.

29. Вероятность случайного события. Под экспериментом (испытанием, опытом) мы будем понимать некоторую воспроизводимую совокупность условий, в которых наблюдается то или другое явление, фиксируется тот или другой результат. Заметим, что "опыт" не обязательно должен быть поставлен человеком; он может протекать независимо от него; при этом человек выступает в роли наблюдателя или фиксатора происходящего от него зависит только решение, что именно наблюдать и какие явления фиксировать. Если результат эксперимента варьируется при его повторении, говорят об опыте со случайным исходом. Именно такие опыты мы будем здесь рассматривать и добавление "со случайным исходом" для краткости опускать. Тот факт, что при повторении опыта его основные условия сохраняются, и, значит, мы вправе ожидать устойчивости частот, тоже не будет каждый раз оговаривать. Случайным событием (или, короче, просто событием) называется всякий факт, который в опыте со случайным исходом может произойти или не произойти. События мы будем обозначать большими буквами латинского алфавита. Для примера рассмотрим несколько событий: 1. Бросание монеты; событие A - появление герба; 2. Бросание трех монет; событие B - появление трех гербов; 3. Передача группы из n сигналов; событие C - искажение хотя бы одного из них; 4. Выстрел по мишени; событие D – попадание; 5. Вынимание наугад одной карты из колоды; событие Е - появление туза; 6. Тот же опыт, что в примере 5; событие F - появление карты червонной масти. Характеризуя вероятности событий числами, нужно установить какую-то единицу измерения. В качестве такой единицы естественно взять вероятность достоверного события, т.е. такого события, которое в результате опыта неизбежно должно произойти. Пример достоверного события - выпадение не более шести очков при бросании игральной кости. Другой пример достоверного события: "камень, брошенный вверх рукой, вернется на Землю, а не станет её искусственным спутником". Если приписать достоверному событию вероятность, равную единице, а невозможному - равную нулю, то все другие события - возможные, но не достоверные будут характеризоваться вероятностями, лежащими между нулем и единицей, составляющими какую то долю единицы. Таким образом, установлены единица измерения вероятности - вероятность достоверного события и диапазон вероятностей - числа от нуля до единицы.

30. Сложение и умножение вероятностей случайных событий. Теоремы сложения вероятностей.Теорема сложения вероятностей несовместных событий.Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:P(A+B)=P(A)+P(B);

P(+А1 +А2…+Ан)=P(А1)+P(А2)+…+P(Ан). Теорема сложения вероятностей совместных событий.

Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления: P(A+B)=P(A)+P(B)-P(AB). Для трех совместных событий имеет место формула: P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC). Событие, противоположное событию A (т.е. ненаступление события A), обозначают А. Сумма вероятностей двух противоположных событий равна единице: _ P(A)+P(А)=1. Вероятность наступления события A, вычисленная в предположении, что событие B уже произошло, называется условной вероятностью события A при условии B и обозначается РВ(A) или P(A/B). Если A и B – независимые события, то P(B)-РА(B)=РА(B). (А-штрих). События A,B,C,… называются независимыми в совокупности, если вероятность каждого из них не меняется в связи с наступлением или ненаступлением других событий по отдельности или в любой их комбинации. Теоремы умножения вероятностей. Теорема умножения вероятностей независимых событий. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий: P(AB)=P(A)•P(B). Вероятность появления нескольких событий, независимых в совокупности, вычисляется по формуле: P(А1А2…Ан)=P(А1)•P(А2)… P(Ан).

Теорема умножения вероятностей зависимых событий. Вероятность совместного появления двух зависимых событий равна произведению одного из них на условную вероятность второго: P(AB)=P(A)• РА(B)=P(B)•РВ(A)

31. Гистограмма, правила построения и интерпретации. Применяется везде, где требуется проведение анализа точности и стабильности процесса, наблюдение за качеством продукции, отслеживание существенных показателей производства. Гистограмма - один из инструментов статистического контроля качества. Японский союз ученых и инженеров в 1979 г. включил гистограммы в состав семи методов контроля качества. Цель - Контроль действующего процесса и выявление проблем, подлежащих первоочередному решению. Один из наиболее распространенных методов, помогающих интерпретировать данные по исследуемой проблеме. Благодаря графическому представлению имеющейся количественной информации, можно увидеть закономерности, трудно различимые в простой таблице с набором цифр, оценить проблемы и найти пути их решения. Для осмысления качественных характеристик изделий, процессов, производства (статистических данных) и наглядного представления тенденции изменения наблюдаемых значений применяют графическое изображение статистического материала, т. е. строя гистограмму распределения. Гистограмма - один из вариантов столбиковой диаграммы, позволяющий зрительно оценить распределение статистических данных, сгруппированных по частоте попадания в определенный (заранее заданный) интервал. Порядок построения гистограммы: 1) Собрать данные, выявить максимальное и минимальное значения и определить диапазон (размах) гистограммы. 2) Полученный диапазон разделить на интервалы, предварительно определив их число (обычно 5-20 в зависимости от числа показателей) и определить ширину интервала. 3) Все данные распределить по интервалам в порядке возрастания: левая граница первого интервала должна быть меньше наименьшего из имеющихся значений. 4) Подсчитать частоту каждого интервала. 5) Вычислить относительную частоту попадания данных в каждый из интервалов. 6) По полученным данным построить гистограмму - столбчатую диаграмму, высота столбиков которой соответствует частоте или относительной частоте попадания данных в каждый из интервалов: наносится горизонтальная ось, выбирается масштаб и откладываются соответствующие интервалы; затем строится вертикальная ось, на которой также выбирается масштаб в соответствии с максимальным значением частот.

32. Кумулятивная гистограмма, правила построения и интерпретация. Кумулята (кумулятивная кривая) представляет собой кривую накопленных частот (частостей). Для ее построения на оси абсцисс откладывают значения аргумента, а на оси ординат – накопленные частоты или накопленные относительные частоты. Масштаб на каждой оси выбирают произвольно.Далее строят точки, абсциссы которых равны вариантам (в случае дискретных рядов) или верхним границам интервалов (в случае интервальных рядов), а ординаты – соответствующим накопленным частотам. Эти точки соединяют отрезками прямой. Полученная ломаная и является кумулятой.

 

33. Нулевая и конкурирующая гипотезы, примеры статистических гипотез, принцип проверки. Можно сравнить две любые совокупности в ходе исследования мы устанавливаем на сколько отличаются друг от друга их статистические показатели, сравнение делаем по принципу нулевой гипотезы, первоначально принимая что различий нет, т.е. две совокупности составляют однородный материал. Они составляют одну общую совокупность. Результат анализа должен подтвердить или опровергнуть гипотезу. Но т.к. различия между статистическими показателями связаны с определённой вероятность ошибки. Между двумя выборами нулевая гипотеза сводится к признанию что две выборки являются сущностью одной совокупности и наблюдаемая разница в целом чисто случайна, т.е. лежит в пределах ошибки, чтобы отвергнуть нулевую гипотезу надо доказать что разница достоверна. Разница работает если в группе более 30 значений. Существование конкурирующих предположений, описывающих или объясняющих один и тот же объект (группу объектов), не только вполне совместимо с познавательной функцией гипотезы, но и прямо вытекает из природы проблемной ситуации. Одновременная (как бы параллельная) разработка нескольких гипотез — типичная форма развития некоторого фрагмента знания, причем достаточно часто гипотезы содержат несовместимые положения, предполагают взаимоисключающие решения одной и той же проблемы. Конкурирующие гипотезы могут разрабатываться не только разными людьми (например, группами ученых), но и одним и тем же субъектом познания. Поведение человека, выдвигающего (допускающего) противоречащие предположения, вследствие характерной для гипотез модальной квалификации не является противоречивым. Конструкция р противоречива и, следовательно, алогична; однако этого нельзя сказать о конструкции. Различают простые и сложные гипотезы. Гипотезу называют простой, если она однозначно характеризует параметр распределения случайной величины. Например, если l является параметром экспоненциального распределения, то гипотеза Н0 о равенстве l =10 – простая гипотеза. Сложной называют гипотезу, которая состоит из конечного или бесконечного множества простых гипотез. Сложная гипотеза Н0 о неравенстве l >10 состоит из бесконечного множества простых гипотез Н0 о равенстве l =bi, где bi – любое число, большее 10. Гипотеза Н0 о том, что математическое ожидание нормального распределения равно двум при неизвестной дисперсии, тоже является сложной. Сложной гипотезой будет предположение о распределении случайной величины Х по нормальному закону, если не фиксируются конкретные значения математического ожидания и дисперсии.

34. Уравнение регрессии. Регрессионный анализ – статистический метод, используемый для исследования отношений между двумя величинами. Регрессия в математической статистике – взаимосвязь среднего значения одной величины от другой величины. В отличие от строгой функциональной величины в регрессионной модели одному и тому же значению величины могут соответствовать несколько значений величины, иными словами, при фиксированном значении х величина у имеет некоторое случайное распределение. Регрессионный анализ используется для определения общего вида уравнения регрессии, оценки параметров этого уравнения, а также проверки различных статистических гипотез относительно регрессии. Регрессионная модель основана на предположении о том, что величина х является контролируемой величиной, значений, которые задаются во время эксперимента, а величина является наблюдаемой в ходе эксперимента. Необходимо отметить, что в том случае, если величина х также является случайной, то для изучения связи между величинами используются методы корреляционного анализа. Уравнение регрессии тем лучше описывает корреляционную зависимость, чем ближе она к линейной и чем больше её достоверность. В случае не линейной зависимости математически запись может выражаться в виде сложных уравнений различных кривых линий.

35. Условия выбора критерия для сравнения средних арифметических. Условия: 1) зависимы или независимы сравниваемые выборы; 2) даны ли сами выборки или только их параметры распределения; 3) не задана ли одна из средних величин точным значением; 4) является ли закон распределения выборки нормальным (если «да» - параметрический критерий, «нет» - непараметрический критерий); 5) равны ли дисперсии выборок. Чаще всего используют непараметрические критерии, в том числе расчет непараметрической доверит. интервала.

36.Ранжирование вариационного ряда. Вариационным рядом называется ранжированный в порядке возрастания или убывания ряд вариантов с соответствующими им частотами или частями. В зависимости от вида вариации может быть дискретным или интервальным. Вариационный ряд называется дискретным, если любые его варианты отличаются на постоянную величину, и интервальным, если варианты могут отличаться один от другого на сколь угодно малую величину. Интервалы в ряду могут быть как равными, так и неравными. Это зависит от характера статистических данных и задач исследования. Ранжированный ряд - это распределение отдельных единиц совокупности в порядке возрастания или убывания исследуемого признака. Ранжирование позволяет легко разделить количественные данные по группам, сразу обнаружить наименьшее и наибольшее значения признака, выделить значения, которые чаще всего повторяются.

Метод попарных сравнений.

Метод попарных сравнений — один из инструментов оценки и выбора решений, широко используется в экспертных оценках при необходимости расставлять приоритеты в процессе какой-либо деятельности или ранжирования различных объектов. Идея метода состоит в том, что попарно сравниваются каждые два объекта и определяется первенство одного из них, отсюда название — «попарное (или парное) сравнение». Считается, что при решении проблемы гораздо легче сделать качественное сравнение двух объектов, опираясь на мнение экспертов, чем установить количественные критерии. Строго говоря, метод ПС — это метод получения исходных данных, метод своеобразного опроса респондентов. На базе полученных данных можно решать разные задачи, совсем необязательно включающие в себя построение оценочной шкалы. Предположим, что нас интересует, как респонденты изучаемой совокупности оценивают какие-либо объекты — профессии, политических лидеров, радиопередачи, какие-то виды товаров и т.д. Обозначим эти объекты через а1, а2,..., аn (n — количество оцениваемых объектов). Рассматриваемый метод позволяет получить ответ на этот вопрос в довольно своеобразном виде. Каждому респонденту предлагаются всевозможные пары, составленные из рассматриваемых объектов. Он должен относительно каждой пары сказать, какой объект из этой пары ему нравится больше. Скажем, в случае рассмотрения в качестве наших объектов некоторых профессий — к примеру, токаря, пекаря, лекаря и т.д. — мы спрашиваем у каждого респондента, какая профессия ему больше нравится: токарь или пекарь (фиксируем ответ), токарь или лекарь (фиксируем ответ), пекарь или лекарь (фиксируем ответ) и т.д. для всех возможных пар рассматриваемых объектов.

38.Основные статистические характеристики положения центра ряда. Среднее арифметическое заменяется индивидуальным варьированием изменения признаков отдельных членов совместимости. При большем количестве вариантов более выгодно пользоваться сгруппированными данными, т.к. это позволяет лучше высчитать важные статистические характеристики и изолировать ошибки вычислений. Свойства: 1) если каждую величину, для которой вычисление х увеличивается или уменьшается на одну и туже величину, то и х увеличивается или уменьшается на туже величину; 2) алгебраичная сумма отклонений вариантов от х=0, т.е. она является равнодействующим показателем для всех варьирующих величин совместимости и даёт возможность проверить правильную х; 3) сумма квадратов отклонений от х< суммы квадратов отклонений от другой величины не равной х. Медиана – это значения варианта, которое точно в середине упорядоченного вариационного ряда. Для нахождения медианы нужно курс построить по росту, выбрать человека стоящего посередине ряда. Если их чётное количество, то берут 2 людей стоящих в середине и находят среднее значение.

39. Функциональная и статистическая взаимосвязь. В спортивных исследованиях между изучаемыми показателями часто обнаруживается взаимосвязь. Функциональная взаимосвязь – каждому показателя соответствует строго определённое значение другого. Статистическая взаимосвязь – когда одному значению одного показателя соответствует несколько значений другого. Это позволяет вскрыть некоторые закономерности и в дальнейшем описать их как словесно, так и математически с целью использования в практической работе тренера или педагога. Среди статистических взаимосвязей наиболее важны корреляционные, потому что средняя величина одного показателя изменяется в зависимости от значения другого. Статистический метод, который используется для исследования взаимосвязей, называется корреляционным анализом. Основной задачей его является определение формы тесноты и направленности изучаемых показателей. Корреляционный анализ позволяет исследовать только статистическую взаимосвязь. Используется в теории тестов для оценки надёжности и информативности.

40. Две основные задачи теории корреляции, виды коэффициентов корреляции. Связь с изменчивостью разнородных признаков называется корреляцией. Первая задача теории корреляции — установить форму корреляционной связи, т. е. вид функции регрессии (линейная, квадратичная показательная и т. д.). Наиболее часто функции регрессии оказываются линейными. Если обе функции регрессии /(*) и ф((/) линейны, то корреляцию называют линейной-, в противном случае — нелинейной. Очевидно, при линейной корреляции обе линии регрессии являются прямыми линиями. Вторая задана теории корреляции — оценить тесноту (силу) корреляционной связи. Теснота корреляционной зависимости К от X оценивается по величине рассеяния зна­чений У вокруг условного среднего ух. Большое рассеяние свидетельствует о слабой зависимости К от X либо об отсутствии зависимости. Малое рассеяние указывает наличие достаточно сильной зависимости; возможно даже, что У и X связаны функционально, но под воздействием второстепенных случайных факторов эта связь оказалась размытой, в результате чего при одном и том же значении х величина Y принимает различные значения. Виды: прямая (положительная) – отображает такую взаимосвязь между признаками, при которой с увеличением первого признака второй тоже увеличивается, обратная (отрицательная) – это взаимосвязь между признаками при которой с увеличением первого признака второй уменьшается. Задачи: 1 установить форму корреляционной связи. Бывает – линейная, квадратичная, показательная. 2 оценить тесноту силы (силу корреляционной связи). Теснота корреляционной зависимости y от x оценивается по величине рассеивания значений.

41. Генеральная и выборочная совокупность (определение и примеры).

Генеральная совокупность – наиболее общая характеристика совокупности объектов объединенных одним признаком. Пример: практически одна и та же случайно отобранная совокупность объектов — коммерческих банков одного административного округа Москвы, может рассматриваться как выборка из генеральной совокупности всех коммерческих банков этого округа, и как выборка из генеральной совокупности всех коммерческих банков Москвы, а также как выборка из коммерческих банков страны и т.д. Генеральная совокупность (а следом за ней и выборочная совокупность) может быть количественной или качественной, что зависит от того, являются ли признаки свойства единиц наблюдения количественным (возраст) или качественным (пол). Это различие предполагает, что статистическое описание совокупности принимает либо форму средних арифметических, либо форму удельного веса (доли). Выборочная совокупность – отборная часть элементов генеральной совокупности, которая представляет всю совокупность с приемлемой точностью. В ходе подготовки к проведению конкретно-социологического исследования на основании теоретических посылок были выделены характеристики и признаки, подлежащие изучению. Например, желание заниматься физической культурой, спортом, величина потребности, участие в видах деятельности и др. На основании результатов изучения этих признаков в пробном исследовании (30 и более респондентов) определяется объем выборки.