
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Реляционная операция соединения. Ее разновидности.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Операция соединения отношений, наряду с операциями выборки и проекции, является одной из наиболее важных реляционных операций. Обычно рассматривается несколько разновидностей операции соединения:
Наиболее важным из этих частных случаев является операция естественного соединения. Все разновидности соединения являются частными случаями общей операции соединения. Общая операция соединения Соединением отношений
Таким образом, операция соединения есть результат последовательного применения операций декартового произведения и выборки. Если в отношениях Тэта-соединение Определение. Пусть отношение
Это частный случай операции общего соединения. Иногда, для операции
Пример. Рассмотрим некоторую компанию, в которой хранятся данные о поставщиках и поставляемых деталях. Пусть поставщикам и деталям присвоен некий статус. Пусть бизнес компании организован таким образом, что поставщики имеют право поставлять только те детали, статус которых не выше статуса поставщика (смысл этого может быть в том, что хороший поставщик с высоким статусом может поставлять больше разновидностей деталей, а плохой поставщик с низким статусом может поставлять только ограниченный список деталей, важность которых (статус детали) не очень высока).
Таблица 1 Отношение A (Поставщики)
Таблица 2 Отношение B (Детали) Ответ на вопрос "какие поставщики имеют право поставлять какие детали?" дает
Таблица 3 Отношение "Какие поставщики поставляют какие детали" Экви-соединение Наиболее важным частным случаем Синтаксис экви-соединения:
Пример. Пусть имеются отношения
Таблица 4 Отношение P (Поставщики)
Таблица 5 Отношение D (Детали)
Таблица 6 Отношение PD (Поставки) Ответ на вопрос, какие детали поставляются поставщиками, дает экви-соединение
Обычно, такой сложной формой записи не пользуются. Но как бы то ни было, в результате имеем отношение:
Таблица 7 Отношение "Какие детали поставляются какими поставщиками" Недостатком экви-соединения является то, что если соединение происходит по атрибутам с одинаковыми наименованиями (а так чаще всего и происходит!), то в результатирующем отношении появляется два атрибута с одинаковыми значениями. В нашем примере атрибуты PNUM1 и PNUM2 содержат дублирующие данные. Избавиться от этого недостатка можно, взяв проекцию по всем атрибутам, кроме одного из дублирующих. Именно так действует естественное соединение. Естественное соединение Определение 10. Пусть даны отношения Тогда естественным соединением отношений Естественное соединение настолько важно, что для него используют специальный синтаксис:
Замечание. В синтаксисе естественного соединения не указываются, по каким атрибутам производится соединение. Естественное соединение производится по всем одинаковым атрибутам. Замечание. Естественное соединение эквивалентно следующей последовательности реляционных операций: 1. Переименовать одинаковые атрибуты в отношениях 2. Выполнить декартово произведение отношений 3. Выполнить выборку по совпадающим значениям атрибутов, имевших одинаковые имена 4. Выполнить проекцию, удалив повторяющиеся атрибуты 5. Переименовать атрибуты, вернув им первоначальные имена Замечание. Можно выполнять последовательное естественное соединение нескольких отношений. Нетрудно проверить, что естественное соединение (как, впрочем, и соединение общего вида) обладает свойством ассоциативности, т.е.
поэтому такие соединения можно записывать, опуская скобки:
Пример. В предыдущем примере ответ на вопрос "какие детали поставляются поставщиками", более просто записывается в виде естественного соединения трех отношений
Таблица 8 Отношение P JOIN PD JOIN D
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 977; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.105.199 (0.006 с.) |

 -соединение (тэта-соединение)
-соединение (тэта-соединение) и
и 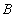 по условию
по условию  называется отношение
называется отношение
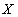 , отношение
, отношение 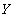 , а
, а 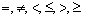 и т.д.). Тогда
и т.д.). Тогда 
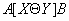
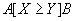 :
: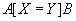
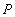 ,
,  и
и 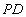 , хранящие информацию о поставщиках, деталях и поставках соответственно (для удобства введем краткие наименования атрибутов):
, хранящие информацию о поставщиках, деталях и поставках соответственно (для удобства введем краткие наименования атрибутов): . На самом деле, т.к. в отношениях имеются одинаковые атрибуты, то требуется сначала переименовать атрибуты, а потом выполнить экви-соединение. Запись становится более громоздкой:
. На самом деле, т.к. в отношениях имеются одинаковые атрибуты, то требуется сначала переименовать атрибуты, а потом выполнить экви-соединение. Запись становится более громоздкой: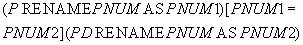
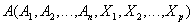 и
и 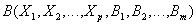 , имеющие одинаковые атрибуты
, имеющие одинаковые атрибуты 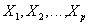 (т.е. атрибуты с одинаковыми именами и определенные на одинаковых доменах).
(т.е. атрибуты с одинаковыми именами и определенные на одинаковых доменах).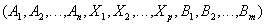 и телом, содержащим множество кортежей
и телом, содержащим множество кортежей 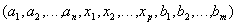 , таких, что
, таких, что  и
и 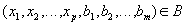 .
.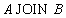
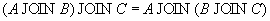
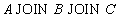
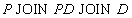 (для удобства просмотра порядок атрибутов изменен, это является допустимым по свойствам отношений):
(для удобства просмотра порядок атрибутов изменен, это является допустимым по свойствам отношений):


