
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамические реакции при вращении тв тела вокруг неподвижной оси.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При движении несвободного твердого тела реакции связей, действующие на это тело, складываются из статических и добавочных динамических составляющих. Re=Reст+Reдин, где Reст − главный вектор статических реакций, Reдин − главный вектор динамических реакций. Статические реакции определяются из уравнений статики, а динамические обусловлены движением тела и определяются только силами инерции. Динамические реакции подшипников при вращении твердого тела вокруг неподвижной оси с учетом принципа д’Аламбера можно определить из следующей системы уравнений
Связи и их уравнения. Классификация связей. По виду своих ур-й связи разделяют на удерживающие и неудерживающие, стационарные и нестационарные. Связь назыв удерживающей или двусторонней если ее ур-е имеет вид строгого равенства. (матем маятник в случае закрепл при пом стержня x2+y2=l2) l –длина стержня, х,у – корд точки. 2 мат точки соед между собой невес жестким стержнем: (x1-x2)2+(y1-y2)2+(z1-z2)2=l2 Если ур-е связи имеет вид равенства-неравенства, то связь – одностор (неудерж). Матем маятник закрепл при пом нити x2+y2≤ l2.Катящееся колесо опорной плоскостью yc-R≥0. Связь (удерж или неуд) назыв стационарной если в ее уравнение время t не входит явным образом, в противном случае связь – нестационарная. Идеальная связь – если возможная работа реакции связи равна 0. Возможные перемещения. Число степеней свободы системы. Виртуальная работа. Идеальные связи Возможные (виртуальные) перемещения системы (ds, dj) — любая совокупность бесконечно малых перемещений точек системы, допускаемых в данный момент наложенными на систему связями. Возможные перемещения рассматривают как величины первого порядка малости, пренебрегая при этом величинами высших порядков малости. Т.е. криволинейные перемещения точек заменяют прямолинейными отрезками, отложенными по касательным к их траекториям. Число независимых между собою возможных перемещений системы называется числом степеней свободы этой системы. Например. шар на плоскости может перемещаться в любом направлении, но любое его возможное перемещение может быть получено как геометрическая сумма двух перемещений вдоль двух взаимно перпендикулярных осей. Свободное твердое тело имеет 6 степеней свободы. Возможная (виртуальная) работа dА — элементарная работа, которую, действующая на матер.точку сила могла бы совершить на возможном перемещении этой точки. Связи являются идеальными, если сумма элементарных работ реакций этих связей при любом возможном перемещении системы равна нулю, т.е. SdАr=0. Принцип возможных перемещений. Этот принцип устанавливает общее условие равновесия механической системы. Согласно этому принципу для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма работ, всех приложенных к системе активных сил на любом возможном перемещении системы была равна нулю. (т.е. говорит о том что сумма работ всех реакций а также сумма всех сил на переем равна нулю). Количество уравнений, которые можно составить для механической системы, исходя из принципа возможных перемещений, равно количеству степеней свободы этой самой механической системы. Общ ур-е динамики. Объединяя принцип Даламбера и принцип возможных перемещений, получим общеe уравнение динамики: при движении системы с идеальными связями в каждый данный момент времен сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы будет равна нулю. Уравнение использует принцип возможных перемещений и принцип Даламбера и позволяет составить дифференциальные уравнения движения любой механической системы. Дает общий метод решения задач динамики. Последовательность составления: а) к каждому телу прикладывают действующие на него задаваемые силы, а также условно прикладывают силы и моменты пар сил инерции; б) сообщают системе возможные перемещения; в) составляют уравнения принципа возможных перемещений, считая систему находящейся в равновесии.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 962; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.12.133 (0.008 с.) |



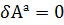
 (сумма работ всех вн сил на возм переем и всех сил инерции на возм переем равна нулю)
(сумма работ всех вн сил на возм переем и всех сил инерции на возм переем равна нулю)


