
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Спектр является периодически сплошнымСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
@42 Какое разностное уравнение соответствует рекурсивному фильтру первого порядка, структурная схема которого показана на рисунке?
4
@2 Какой зависимостью связаны между собой интервал дискретизации T, частота дискретизации fД и наивысшая частота FВ в спектре передаваемого сигнала? 4
Какой импульсной характеристикой обладают нерекурсивные фильтры? Нерекурсивные фильтры (КИХ-фильтры) имеют конечную импульсную характеристику. @41 Какой порядок имеет трансверсальный (нерекурсивный) фильтр, структурная схема которого показана на рисунке?
Первый.
@16 Какой спектр имеет периодический дискретный сигнал? Периодический дискретный сигнал имеет периодический дискретный спектр.
@19 Какой формулой определяется комплексная частота в преобразовании Лапласа? 4
@58 Какую операцию осуществляет эспандер частоты дискретизации? Перед цифровой фильтрацией увеличивает частоту дискретизации исходного сигнала в L раз.
@3 Какую протяженность имеют спектры сигналов, ограниченных во времени (импульсов)? Спектр импульсов бесконечен.
@54 На каком из рисунков приведена каноническая форма рекурсивного фильтра?
б)
4 На рисунке б).
@53 На каком из рисунков приведена параллельная форма рекурсивного фильтра? в)
3 На рисунке в).
На каком рисунке изображен одиночный импульс и его спектр? Ответ рис 1
4 На рис. 1.
@21 На каком рисунке показана плоскость Z, используемая в Z-преобразовании?
2 На рис. 1.
@17 Обратное преобразование Фурье позволяет вычислить? 4 Мгновенное значение импульса s(t), если задана его спектральная плотность Ŝ(ω).
@11 Основное свойство спектра дискретизованного сигнала – одиночного импульса? Спектр является периодическим сплошным.
@40 По какой формуле определяется импульсная характеристика линейной дискретной системы? 2
@6 По какой формуле определяется количество уровней квантования N, если разрядность АЦП (а, следовательно и разрядность кодовой комбинации двоичного кода) равна n? 2 N=2n.
@4 По какому принципу ограничивают при обработке спектры конечных сигналов (импульсов)? 2 Начиная с некоторой FВ пренебрегают теми частотами, на которых амплитуды незначительны.
@49 Почему в рекурсивных фильтрах необходимо увеличивать разрядность представления чисел в линиях задержки по сравнению с разрядностью входного и выходного сигналов? Потому, что абсолютные величины отсчетов, перемещающихся по линии задержки могут существенно превосходить амплитуду входного и выходного сигналов.
@46 Почему рекурсивные фильтры называются БИХ-фильтрами? Потому что за счет обратных связей их импульсная характеристика бесконечна.
@9 Прямое преобразование Фурье позволяет определить? 4 Спектральную плотность Ŝ(ω) импульса s(t). @48 Сколько линий задержки содержит каноническая реализация рекурсивного фильтра? Одну общую линию задержки.
Схема какого фильтра изображена на рисунке?
Прямая реализация рекурсивного фильтра – биквадратный блок. @43 Чем отличается рекурсивный фильтр от нерекурсивного? В рекурсивном фильтре вводятся в схему обратные связи.
@37 Чему равен выходной сигнал y(k), полученный в результате цифровой фильтрации входного сигнала {x(k)}={1,3,2}, если цифровой фильтр имеет импульсную характеристику {h(k)}={1,1,2}? 3 y(k)={1,4,7,8,4}
@33 Чему равна передаточная (системная) функция дискретной цепи H(Z), если ее импульсная характеристика {h(k)}={1, -1, 1}? 4
@20 Чему равна переменная Z в Z-преобразовании? 2
@47 Чему равны первые два отсчета импульсной характеристики h(k) рекурсивного фильтра, структурная схема которого изображена на рисунке?
1 h(0)=a0, h(1)=a1+b1h(0)=a1+a0b1.
@5 Что кодируется после квантования: дискретный отсчет, шаг квантования, номер уровня квантования или номер шага квантования? Номер уровня квантования.
@34 Что называется цифровым фильтром? 3 Алгоритм, обрабатывающий во временной или частотной области входные отсчеты {x(k)} и формирующий выходные отсчеты {y(k)}.
@38 Что определяют функции, входящие в формулу свертки двух функций 1
Что позволяет определить обратное Z-преобразование Ŝ (Z) функции s(t), дискретизованной и заданной множеством отсчетов {x(k)}? 4 Оригинал функции {x(k)}. @@ Что позволяет определить прямое преобразование Фурье?
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 812; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.206.120 (0.007 с.) |


 .
. .
.
 @36
@36
 .
.



 .
. @50
@50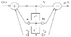
 .
. .
.
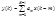 , по которой определяется сигнал на выходе нерекурсивного (КИХ) фильтра?
, по которой определяется сигнал на выходе нерекурсивного (КИХ) фильтра? – ядро фильтра, определяющего его импульсную характеристику,
– ядро фильтра, определяющего его импульсную характеристику,  – входной сигнал;
– входной сигнал;



