
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Для обеспечения совместной работы.Содержание книги
Поиск на нашем сайте
@15 Если TС – длительность импульса, T – шаг дискретизации, N – количество отсчетов сигнала, то по какой формуле определяется количество отсчетов? 2 @32 Если X(Z) – Z-преобразование входного сигнала, Y(Z) – Z-преобразование выходного сигнала, то чему равна передаточная (системная) функция дискретной цепи?
1
@29 Если выходная дискретная последовательность y(k) определяется по формуле Сложение, умножение и задержка.
@12 Если дискретизованный сигнал можно представить в виде взвешенной последовательности дельта-функций формулой 2 {s(kt)}=3δ(t)+2δ(t – 1T)+1δ(t – 2T)+0δ(t – 3T) – 1δ(t – 4T).
@18 Если известен спектр
3
Если частотная характеристика цифрового фильтра является периодической функцией частоты, то чему равен период ее повторения? Частоте дискретизации.
@60 Из каких элементов составляют типовые звенья дискретной цепи? Из сумматоров, умножителей, элементов задержки. @31 Из-за чего возникают неточности при представлении чисел в двоичном коде при цифровой обработке сигналов? Из-за ограниченности разрядности цифровых устройств.
@14 Как должны располагаться сдвинутые копии спектра дискретизованного сигнала для точного восстановления этого сигнала? Сдвинутые копии спектра дискретизованного сигнала не должны перекрываться.
@51 Как запишется алгоритм работы рекурсивного фильтра, изображенного на рисунке?
2
@39 Как изменяется точность обработки сигнала фильтром при увеличении числа отсчетов в его ядре, определяющим импульсную характеристику фильтра? С увеличением числа отсчетов в ядре фильтра точность обработки сигнала повышается.
@57 Как называется процесс преобразования цифрового сигнала от более высокой частоты к более низкой? Децимацией цифрового сигнала.
@56 Как называется процесс преобразования цифрового сигнала от более низкой частоты к более высокой? Интерполяцией цифрового сигнала.
@30 Как называются элементы структурной схемы, изображенные на рисунке?
2 а) – сумматор, б) – умножитель, в) – элемент задержки.
@45 Как определяется порядок рекурсивного цифрового фильтра? Порядок рекурсивного цифрового фильтра определяется коэффициентом нерекурсивной части.
@22 Как перемещается точка Z-плоскости (Z-преобразование), если соответствующая ей точка p-плоскости (преобразование Лапласа) перемещается вдоль оси jω в пределах 4 По единичной окружности
Как связаны спектральные коэффициенты Ŝ( n ) дискретного преобразования Фурье последовательности {x(k)} с Z-преобразованием этой последовательности? 3 Спектральные коэффициенты Ŝ(n) дискретного преобразования Фурье последовательности {s(k)} равны значениям Z-преобразования этой последовательности.
@44 Как формируется выходные отсчеты сигнала в рекурсивном фильтре? Для формирования выходного отсчета используются значения не только этого входного сигнала но и последующего входного.
@27 Как читается теорема линейности Z-преобразования? Сумме дискретных сигналов соответствует сумма их Z-изображений.
@28 Как читается теорема свертки Z-преобразований двух сигналов. 2 Z- преобразованию свертки дискретных сигналов отвечает произведение Z-преобразований этих сигналов.
@52 Какая из приведенных ошибок не относится к ошибкам цифровой фильтрации? Ошибки квантования входных и выходных сигналов. Округление значений входных аналоговых сигналов.
@23 Какая формула соответствует прямому Z-преобразованию дискретного сигнала x(k)? 2
@8 Каким соотношением связано время переработки сигнала в вычислителе tпер с периодом дискретизации T, так, чтобы до поступления нового отсчета все необходимые действия были бы выполнены? 4 tпер ≤ T. @@ Каким является спектр дискретизированного сигнала?
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 798; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |


 .
. , то какие действия в ней выполняются?
, то какие действия в ней выполняются? , то как можно записать последовательность отсчетов {s(kt)}= {3, 2, 1, 0, –1}?
, то как можно записать последовательность отсчетов {s(kt)}= {3, 2, 1, 0, –1}? одиночного импульса
одиночного импульса  , то какая формула позволяет вычислить спектр этого же дискретизованного импульса
, то какая формула позволяет вычислить спектр этого же дискретизованного импульса  ,?
,?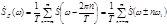 .
.



 ?
? .
. @25
@25



