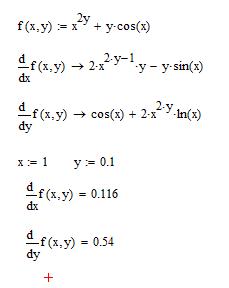Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение поверхностей, полученных при вращении вокруг осейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вращая некоторую кривую вокруг той или иной оси, можно получить интересные объемные фигуры. При этом необходимо обеспечить перерасчет координат точек по известным геометрическим формулам. В MathCAD эту задачу выполняет встроенная функция CreateMesh, использование которой позволяет строить параметрически заданные поверхности. CreateMesh(F (или G, или f1, f2, f3), x0, x1, y0, y1, xgrid, ygrid, fmap) Создает сетку на поверхности, определенной функцией F. x 0, x 1, y 0, y 1– диапазон изменения переменных, xgrid, ygrid - размеры сетки переменных, fmap – функция отображения. Все параметры, за исключением F, факультативные. Функция CreateMesh по умолчанию создает сетку на поверхности с диапазоном изменения переменных от -5 до 5 и с сеткой 20*20 точек. Упражнение. Постройте поверхности кривой f(x)=xsin(x)2 на интервале [-π, 2], полученные при вращении вокруг осей. 1. Постройте заданную кривую f(x)=xsin(x)2 (см. рис. 32).
Рис. 32. Построение кривой 2. Чтобы получить поверхность, полученную при вращении вокруг оси ОХ, нужно записать функцию CreateMesh с параметрами, которые вычисляют по специальным математическим формулам: F(u,v):=u, G(u,v):=f(u)cos(v), H(u,v):=f(u)sin(v), mesh:=30. 3. Присваиваем функцию CreateMesh переменной SX:=CreatMesh(F,G,H,a,b,0,2π,mesh) 4. Выбираем с панели График заготовку для построения трехмерного графика. 5. В левом нижнем углу графической области вводим имя переменной SX и получаем поверхность как на рисунке 33. 6. Чтобы получить поверхность, полученную при вращении вокруг оси ОY, нужно записать функцию CreateMesh с параметрами, которые вычисляют по специальным математическим формулам: X (u,v):=usin(v), Y(u,v):=ucos(v), Z(u,v):=f(u), mesh:=30. 7. Присваиваем функцию CreateMesh переменной SY:=CreatMesh(X,Y,Z,a,b,0,2π,mesh) 8. Выбираем с панели График заготовку для построения трехмерного графика. 9. В левом нижнем углу графической области вводим имя переменной SX и получаем поверхность как на рисунке 33.
Рис. 33. Построение поверхностей Контрольные вопросы 1. Какими способами можно построить двумерный график функции? 2. Какими способами можно построить трехмерный график функции? 3. Как можно отформатировать графическую область и сам график функции? РЕШЕНИЕ УРАВНЕНИЙ Цель: получить навыки решения уравнений в программе MathCad разными способами. Решить уравнение можно несколькими способами. 1. Для решения уравнений вида f(x)=0 можно использовать функцию root(f(x),x), предварительно задав начальное приближение неизвестной переменной. 2. Также для решения уравнений можно использовать функцию polyroots(k), где k – коэффициенты переменной х, стоящие в порядке возрастания степени. Тогда результатом вычислений будет транспонированный вектор l 3. Можно также найти корни уравнения в виде символьного решения, используя меню Symbolіc (Символьно)/Varіable (Переменная)/Solve (Вычислить). Знак логического равно находится на панели Булева алгебра. В результате получим вектор значений корней уравнения. 4. При решении уравнений графическим способом, необходимо построить два графика: левой и правой частей уравнения и найти точки их пересечения. 5. При решении уравнений, систем линейных и нелинейных уравнений можно использовать «блок решений», начинающийся словом Given и заканчивающийся функцией Find(x). В уравнении должно быть использовано логическое равно. 6. В случае, когда функция Find(x) не находит корней уравнения, можно воспользоваться функцией Minerr(x1,x2,…). По своей работе она подобна функции Find(x), но у нее другие условия для итеративного процесса поиска решений. Упражнение. Найти корни уравнения f(x)=5*x2+3*x-7 с помощью функции root. 1. Квадратное уравнение имеет два корня. Введите первое начальное значения для переменной x =-5. 2. Введите функцию f(x), равную заданному выражению: f(x):=5*x2+3*x-7. 3. Находим значение первого корня уравнения с помощью функции root. Введите root(f(x), x)=: 4. Получаем значение первого корня x=-1.521 (смрис. 34). 5. Аналогично находим второй корень уравнения. Присваиваем переменной x приближенное значение 5, то есть x:=5. 6. Вычисляем уточненное значение переменной x с помощью функции root. Введите root(f(x), x)=. 7. Получаем значение второго корня уравнения x=0.921 (см рис. 34).
Рис. 34. Решение уравнения с помощью функции root Упражнение. Найти корни уравнения f(x)=5*x2+3*x-7 с помощью функции polyroots. 1. Введите функцию f(x):=5*x2+3*x-7. 2. Введите значения для вектора k – коэффициенты переменной х, стоящие в порядке возрастания степени, то есть 3. Тогда результатом вычислений будет транспонированный вектор l. То есть вектору l:= polyroots(k), а затем его транспонируем: lT=. 4. В результате мы получим два значения корней уравнения x=-1.521 и x=0.921 (см рис. 35).
Рис. 35. Решение уравнения с помощью функции polyroots Упражнение. Найти корни уравнения f(x)=5*x2+3*x-7 в виде символьного решения. 1. Введите заданное уравнение, приравненное к 0, используя знак логического равно с панели Булева алгебра. 2. Выделив переменную x выполните команду Solve (Вычислить /Решить) подпункта меню Varіable (Переменная) меню Symbolіc (Символьно). 3. В результате получим вектор значений корней уравнения (рис. 36)
Рис. 36. Символьное решение уравнения Упражнение. Найти корни уравнения f(x)=5*x2+3*x-7 с помощью «блока решений», начинающегося словом Given и заканчивающегося функцией Find(x). 1. Введите начальное значение для искомой переменной: x:=-2. 2. Введите слово Given. 3. Введите заданное уравнение, приравненное к 0, используя знак логического равно с панели Булева алгебра. 4. Введите Find(x) =. Получим значение первого корня уравнения. Аналогично найдем второй корень уравнения. 5. Введите начальное значение для искомой переменной: x:=1. 6. Введите слово Given. 7. Введите заданное уравнение, приравненное к 0, используя знак логического равно с панели Булева алгебра. 8. Введите Find(x) =. Получим значение второго корня уравнения. (см рис. 37).
Рис. 37. Решение уравнений с помощью «блока решений» Упражнение. Найти корни уравнения f(x)=5*x2+3*x-7 с помощью «блока решений», начинающегося словом Given и заканчивающегося функцией Minerr(x1,x2,…). 1. Введите начальное значение для искомой переменной: x:=-2. 2. Введите слово Given. 3. Введите заданное уравнение, приравненное к 0, используя знак логического равно с панели Булева алгебра/Логический. 4. Введите Minerr (x) =. Получим значение первого корня уравнения. Аналогично найдем второй корень уравнения. 5. Введите начальное значение для искомой переменной: x:=1. 6. Введите слово Given. 7. Введите заданное уравнение, приравненное к 0, используя знак логического равно с панели Булева алгебра/Логический. 8. Введите Minerr (x) =. Получим значение второго корня уравнения. (см рис. 38).
Рис. 38. Поиск решения с помощью функции Minerr(x1,...) Контрольные вопросы 1. Какими способами можно решить уравнение? 2. В чем разница между функциями root и polyroots? 3. В чем разница между функциями Find и Minerr? 4. Как находится символьное решение корней уравнения?
РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ Цель: научиться решать системы уравнений в программе MathCad различными способами. Решать системы уравнений также можно несколькими способами. 1. При решении системы линейных уравнений с помощью функции lsolve(M,m), где M – квадратная, невырожденная матрица, а m – вектор свободных членов уравнений, стоящих справа от знака равно. Результатом будет вектор решений системы уравнений. 2. Решить систему уравнений можно в символьном виде при помощи функции soln. В результате будет получен вектор с найденными значениями неизвестных. 3. Также систему уравнений можно решить с помощью «блока решений» и функций Find() и Minerr(). Упражнение. Решить систему уравнений 1. Введите матрицу M, состоящую из коэффициентов x. 2. Введите вектор m – вектор свободных членов уравнений, стоящих справа от знака равно. 3. Для решения системы линейных уравнений введите функцию lsolve (M,m)=. Результатом будет вектор решений системы уравнений (рис. 39).
Рис. 39. Решение системы уравнений с помощью функции lsolve
Упражнение. Решить систему уравнений 1. Введите матрицу M, состоящую из коэффициентов x. 2. Введите вектор m – вектор свободных членов уравнений, стоящих справа от знака равно. 3. Введите формулу soln:=M-1m. 4. Введите soln=. В результате будет получен вектор с найденными значениями неизвестных (см рис. 40).
Рис. 40. Решение систем уравнений с помощью функции soln
Упражнение. Решить систему уравнений 1. Введите начальные значения для переменных: k:=0, l:=0, m:=0,n:=0. 2. Введите заданные уравнения, используя логическое равно с панели Булева алгебра/Логический. 3. Для решения системы введите функцию Find(k, l, m, n)=. Вектор решения можно увидеть на рис. 41.
Рис. 41. Решение систем уравнений с помощью «блока решений» и функции Find() Упражнение. Решить систему уравнений 1. Введите начальные значения для переменных: k:=0, l:=0, m:=0,n:=0. 2. Введите заданные уравнения, используя логическое равно с панели Булева алгебра/Логический. 3. Для решения системы введите функцию Minerr(k, l, m, n)=. Вектор решения можно увидеть на рисунке 42.
Рис. 42. Решение систем уравнений с помощью «блока решений» и функции Minerr()
Упражнение. Решить систему нелинейных уравнений 1. Введите начальные значения для переменных: k:=0, l:=0. 2. Введите заданные уравнения, используя логическое равно с панели Булева алгебра/Логический. 3. Для решения системы введите функцию Find(k, l)=. Вектор решения можно увидеть на рисунке 43.
Рис. 43. Решение систем нелинейных уравнений с помощью функции Find()
Упражнение. Решить систему нелинейных уравнений 1. Введите начальные значения для переменных: k:=0, l:=0. 2. Введите заданные уравнения, используя логическое равно с панели Булева алгебра/Логический. 3. Для решения системы введите функцию Minerr(k, l)=. Вектор решения можно увидеть на рисунке 44.
Рис. 44. Решение системы нелинейных уравнений с помощью функции Minerr()
Контрольные вопросы 1. Какими способами можно решить систему уравнений? 2. В чем отличие функций soln и lsolve? 3. Как могут быть представлены результаты решения систем уравнений? ДЕЙСТВИЯ С МАТРИЦАМИ Цель: научиться выполнять различные действия над матрицами в программе MathCad. Чтобы создать матрицу нужно на панели Матрицы нажать кнопку Матрица или вектор, и в появившемся окне указать необходимое количество строк и столбцов. Над матрицами можно производить действия как в символьном виде, так и вычислительные, используя пункт меню Symbolіc (Символьно), подпункт меню Matrіx (Матрица), а также панели Матрицы и Символьно. Существует ряд встроенных векторных и матричных функций. К векторным функциям, встроенным в MathCad, относятся: - lenght (V) – возвращает длину вектора; - last(V) – возвращает индекс последнего элемента; - max(V) – возвращает максимальный по значению элемент; - min(V) – возвращает минимальный по значению элемент. - К матричным функциям, встроенным в MathCad, относятся: - аugment (А1, А2) – объединяет в одну матрицы А1 и А2, имеющие одинаковое число строк (объединение идёт “бок о бок”); - identity (n) – создаёт единичную квадратную матрицу размером n*n; - stack (А1, А2) – объединяет в одну матрицы А1 и А2, имеющие одинаковое число столбцов, располагая А1 над А2; - diag (V) – создаёт диагональную матрицу, элемент главной диагонали которой – вектор V. Специальные характеристики матриц возвращаются следующими функциями: - cols (А) - возвращает число столбцов матрицы А; - rows (А) - возвращает число строк матрицы А; - rank (А) - возвращает ранг матрицы А; - mean (А) - возвращает среднее значение элементов массива А. Упражнение. Найти в символьном виде определитель матрицы, обратную и транспонированную матрицы. Создаем матрицы из коэффициентов p, q, r, s, t, u. Выделив полученную матрицу синей рамкой, применить необходимые операции нахождения определителя, нахождения обратной матрицы и нахождения транспонированной матрицы с панели Символьно или из пункта меню Символьно подпункта Матрица. Результат представлен на рисунке 45.
Рис. 45. Действия с матрицами в символьном виде
Вычислить: - L-p*H; - K*L; - H2; - H-1; - L*H; - K*N; - L*N; - L+3; - ранги матриц L, M, K. Введите значения для переменных: p:=2, q:=4, r:=1, s:=3, t:=5,u:=6. Заполните матрицы коэффициентами p, q, r, s, t, u как на рис. 46.
Рис. 46. Создание матриц
Чтобы произвести вычисления, нужно набрать соответствующее действие и нажать знак равно. Ранг матрицы вычисляется с помощью функции rank(M). Сверьте результат с рисунком 47.
Рис. 47. Результаты вычислений
Упражнение. Решить систему линейных уравнений 1. Вводим матрицу А, состоящую из коэффициентов, стоящих перед x1, x2, x3. 2. Вводим вектор b, состоящий из свободных членов. 3. Вычисляем определитель матрицы А, используя кнопку Определитель на панели Матрица. 4. Так как определитель матрицы А отличен от нуля, система имеет единственное решение. 5. Находим значения x по формуле: x:=A-1b. 6. Получаем результат: x1=2, x2=1, x3=3 (см. рис. 48).
Рис. 48. Решение системы уравнений методом Крамера Контрольные вопросы 1. Как создаются матрицы и векторы? 2. Какие операции можно выполнять с матрицами? ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ Цель: получить навыки вычисления производных и решения производных в задачах геометрии и частных производных. Вычисление производных Для вычисления производных и интегралов в MathCad используется панель Высшая математика. Для дифференцирования в MathCad существует два метода: численный и символьный. В результате символьного метода получаем функцию, которую можно использовать в будущих расчетах. Численный метод используется в некоторых специфических задачах. В MathCadе имеется возможность вычислять обычные производные, производные высоких порядков и частные производные с помощью панели Высшая математика. Для ввода производной первого порядка в верхний маркер вводится функция, а в нижний – переменная, по которой нужно вычислить производную. Чтобы получить результат в символьном виде, можно использовать оператор символьного вывода ® или подпункт меню Evaluate \ Вычислить символьно в меню Symbolic \ Символьно. Так же можно использовать операторы с панели Символьно. При использовании оператора simplify \ упростить выражение, результат получаем в неупрощенном виде. Чтобы упростить полученное выражение, можно использовать оператор collect \ приведение подобных членов полинома, factor \ разложение выражения на множители, expand \ раскрытие скобок. Производные первого и второго порядка встречаются в задачах геометрии при составлении уравнений касательно и нормали к прямой, заданной уравнением y(x)=f(x) в точке А(x0,y0). Упражнение. Вычислить производную f’(x)=2-xsin(x)-e4x в символьном виде. 1. Чтобы начать набирать производную, нажмите на кнопку Производная панели Исчисление. В нижний маркер введите x – переменная, по которой нужно найти производную. В верхний маркер введите заданное выражение. 2. Чтобы получить результат в символьном виде, используйте оператор символьного вывода ® или подпункт меню Evaluate \ Вычислить символьно в меню Symbolic \ Символьно. Так же можно использовать операторы с панели Символьно. 3. Примените к полученному выражению оператор simplify \ упростить выражение, в результате получим выражение в неупрощенном виде. Чтобы упростить полученное выражение, воспользуйтесь оператором collect \ приведение подобных членов полинома, factor \ разложение выражения на множители, expand \ раскрытие скобок (рис. 49).
Рис. 49. Символьное вычисление производной
Упражнение. Вычислить производную f’(x)=x-3x2 в численном виде. 1. Введите заданную производную, используя кнопку Производная панели Исчисления. 2. Вычислите производную в символьном виде, используя оператор символьного вывода ® или подпункт меню Evaluate \ Вычислить символьно в меню Symbolic \ Символьно. 3. Присвойте значение переменной x:=5. 4. Скопируйте символьный результат производной и вычислите его символьно (рис. 50).
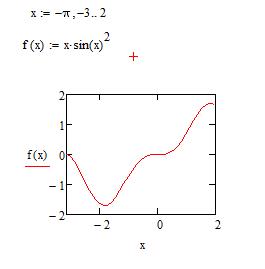
Рис. 50. Численное вычисление производной Упражнение. Вычислите частные производные функции f(x,y)=x2y+ycos(x) в символьном виде и вычислите их при x=1 и y=0.1. 1. Введите заданную функцию f(x,y):=x2y+ycos(x). 2. Вычислите производную функции f(x,y) по x в символьном виде. 3. Вычислите производную функции f(x,y) по y в символьном виде. 4. Введите заданные значения: x:=1, y:=0.1. 5. Вычислите производные для заданных значений. Результат сравните с рисунком 51.
Рис. 51. Вычисление производных
Упражнение. Вычислите производные второго порядка в символьном виде функции f(x,y)=x2y+ycos(x). 1. Введите заданную функцию f(x,y):=x2y+ycos(x). 2. Вычислите вторую производную функции f(x,y) по x в символьном виде. 3. Вычислите вторую производную функции f(x,y) по y в символьном виде. 4. Вычислите смешанную производную функции f(x,y). 5. Введите заданные значения: x:=1, y:=0.1. 6. Вычислите производные для заданных значений. Результат сравните с рисунком 52.
Рис. 52. Вычисление вторых производных
|
||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 543; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.4.50 (0.008 с.) |

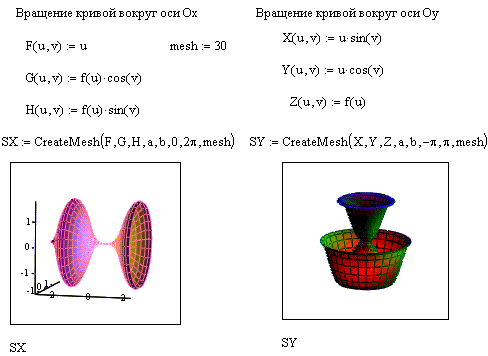
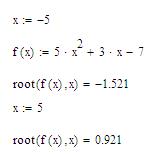
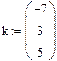 .
.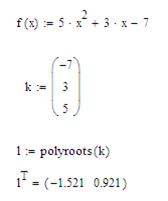
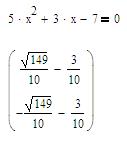
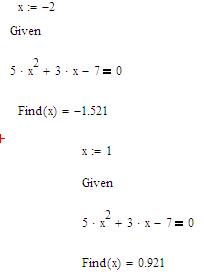
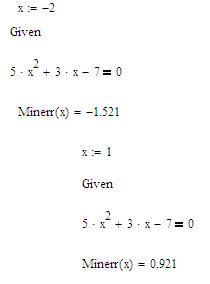
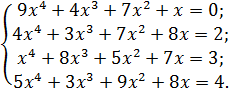 с помощью функции lsolve.
с помощью функции lsolve.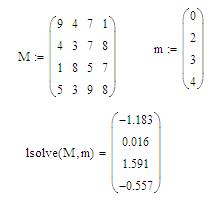

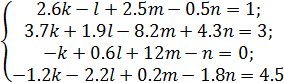 с помощью «блока решений» и функции Find().
с помощью «блока решений» и функции Find().

 с помощью функции Find().
с помощью функции Find().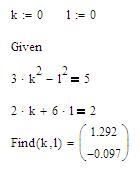
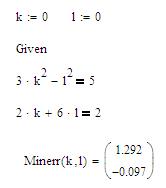
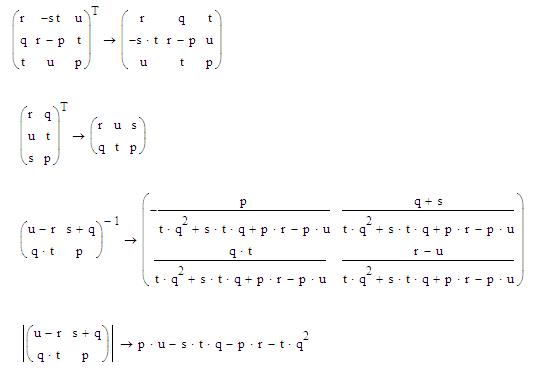
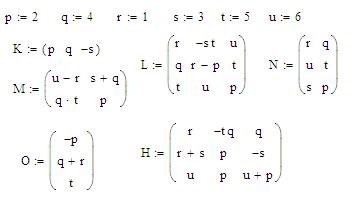

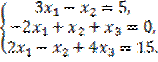 методом Крамера
методом Крамера