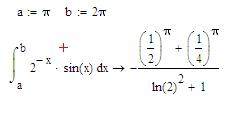Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление производных в задачах геометрии и частных производныхСодержание книги
Поиск на нашем сайте
Упражнение. Составить уравнения касательной и нормали к линии, заданной уравнением y(x)= х3 -3х2-5х+1 в точке А(2,-3) и построить их графики. 1. Присвойте значения для х0 и у0: х0:=2, у0:=-3. 2. Запишите уравнение прямой y(x):= х3 -3х2-5х+1. 3. Вычислите символьно первую производную функции у(х), используя оператор символьного вывода ® или подпункт меню Evaluate \ Вычислить символьно в меню Symbolic \ Символьно. 4. Запишите производную второй степени yy(x), используя кнопку N -Производная с панели Исчисления. Вычислите символьно вторую производную, используя оператор символьного вывода ® или подпункт меню Evaluate \ Вычислить символьно в меню Symbolic \ Символьно. 5. Найдите уравнение касательной. Введите формулу: 6. Находите уравнение нормали. Введите формулу: 7. Постройте графики касательной и нормали (рис. 53).
Рис. 53. Решение задач геометрии
Упражнение. Дана функция y(x, q, z)=xex+z2-q3x3z3. Вычислить числовое и символьное значение частных производных второго порядка. Для этого нужно сделать следующее: 1. Запишите уравнение y(x, q, z):=xex+z2-q3x3z3 2. Запишите производную второй степени для каждой переменной, используя кнопку N -Производная с панели Исчисления. 3. Выберите в контекстном меню View Derivative As \Показать производную как, установите флажок Partial Derivative \(Частная производная (рис. 54)
Рис. 54. Меню «Показать производную как» 4. С помощью оператора символьного вычисления ® или подпункта меню Evaluate \ Вычислить символьно в меню Symbolic \ Символьно найдите производные второго порядка в символьном виде. 5. Задайте числовые значения переменным: x:=1, q:=1, z:=1. Вычислите производные в численном виде. Результат представлен на рисунке 55.
Рис. 55. Вычисление частных производных высшего порядка Контрольные вопросы 1. Какими способами можно вычислить производные? 2. Как составить уравнение касательной к прямой в заданной точке? 3. Как составить уравнение нормали к прямой в заданной точке? ВЫЧИСЛЕНИЕ ИНТЕРГАЛОВ Цель: получить навыки вычисления интегралов и вычисления интегралов в задачах геометрии. Вычисление интегралов Для ввода неопределенного интеграла необходимо ввести в левый маркер функцию (или имя функции), а под знак дифференциала – переменную интегрирования. Для упрощения полученного выражения, так же как при дифференцировании, используются операторы simplify \ упростить выражение, collect \ приведение подобных членов полинома, factor \ разложение выражения на множители, expand \ раскрытие скобок. К полученному в результате интегрирования выражению можно применять несколько символьных операторов. Для нахождения определенного интеграла добавляются в соответствующих местах границы интегрирования. Для нахождения кратных интегралов на месте введения функции вводится еще один оператор интегрирования, границы интегрирования и функция. Также вычисляется интегрирование по нескольким переменным. Для получения результата интегрирования в символьном виде используются те же способы, что и при дифференцировании. Чтобы получить численный результат интегрирования, необходимо задать числовые значения границам интегрирования и, вызвав контекстное меню, выбрать метод интегрирования (рис. 56).
Рис. 56. Методы интегрирования Вычисление интегралов используется при решении задач геометрии и механики, таких как нахождение площади плоской фигуры и координат центра тяжести пластины, ограниченных линиями. Упражнение. Вычислить неопределенный интеграл 1. С помощью кнопки Неопределенный интеграл с панели Исчисление введите заданный интеграл. 2. Вычислите интеграл в символьном виде, используя оператор символьного вывода. Сравните с результатом на рисунком 57.
Рис. 57. Вычисление неопределенного интеграла
Упражнение. Вычислите неопределенный интеграл в символьном виде функции 3. С помощью кнопки Неопределенный интеграл с панели Исчисление введите заданный интеграл. Вычислите интеграл в символьном виде, используя оператор символьного вывода. Сравните с результатом на рисунком 58.
Рис. 58. Вычисление неопределенного интеграла
Упражнение. Вычислить определенный интеграл 1. Введите заданный интеграл, используя кнопку Определенный интеграл с панели Исчисления. 2. Вычислите интеграл в символьном виде, используя оператор символьного вывода. 3. Упростите полученное выражение с помощью операторов simplify \ упростить выражение, collect \ приведение подобных членов полинома, factor \ разложение выражения на множители, expand \ раскрытие скобок. К полученному в результате интегрирования выражению можно применять несколько символьных операторов. Результат представлен на рисунке 59.
Рис. 59. Вычисление определенного интеграла в символьном виде
Упражнение. Вычислить определенный интеграл 1. Введите значения границ интегрирования: a:=π, b:=2π. 2. Введите заданный определенный интеграл. 3. Вычислите интеграл, используя оператор логического вывода. Результат на рисунке 60.
Рис. 60. Вычисление интеграла численным методом
|
||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 253; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.9.183 (0.006 с.) |

 . Используя оператор символьного вывода ®, получите уравнение касательной.
. Используя оператор символьного вывода ®, получите уравнение касательной. . Используя оператор символьного вывода ®, получите уравнение нормали.
. Используя оператор символьного вывода ®, получите уравнение нормали.


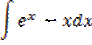 .
.
 .
.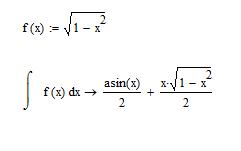
 в символьном виде.
в символьном виде.