Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перетворення Лежандра. Нерівність юнга. Двоїсті за Юнгом функції. Теорема Донкіна. Теореми Лагранжа і Кастільяно
Перетворення Лежандра – допоміжний математичний прийом, який полягає у переході від функцій на лінійному просторі до функцій на спряженому просторі. Воно аналогічно проективній подвійності і тангенціальним координатам у алгебраїчній геометрії або побудові спряженого банахова простору в математичному аналізі. Нехай Перетворення Лежандра функції
Дві функції
Теорема. Перетворення Лежандра інволютивне, тобто його квадрат дорівнює тотожному перетворенню: якщо Доведення. Щоб здійснити перетворення Лежандра функції
знайти точку
і тоді перетворення Лежандра
Зафіксуємо тепер Слідство. Нехай дано сімейство прямих
Стосовно цього прикладу зазначимо, що рівність
і має min при Функції
Приклад 2 Для форми Доведення. З теореми Ейлера про однорідні функції
Отже, Випадок багатьох змінних. Нехай тепер
Усі попередні міркування, в тому числі нерівність Юнга, без змін переносяться на цей випадок. Отже, функції Аналогічні висновки можна зробити і при нелінійній залежності
Робота зовнішніх сил
При цьому
Основна інтегральна формула (формула Гріна):
Тоді отримаємо
відомий вираз для теореми Клапейрона.
При
При
Функції потенціальної енергії пружної деформації
Другі похідні від потенціальної енергії пружної деформації по переміщенню і від додаткової потенціальної енергії по відповідній дорівнюють відповідно коефіцієнтам матриці жорсткості та матриці піддатливості. Теорема Донкіна Нехай задана деяка функція
і нехай існує перетворення змінних, викликане функцією
Тоді існує перетворення, зворотне до перетворення (2), яке теж породжено деякою функцією
при цьому функція Y, що породжує функцію зворотного перетворення, пов’язана з функцією Х, що породжує пряме перетворення, формулою:
Якщо функція включає параметри
Доведення. Гесіан функції X співпадає з якобіаном правих частин у рівнянні (2). Тому умова (1) показує, що з рівняння (2) показати змінні
Нехай функція
Але згідно рівняння (2), два доданки, які знаходяться в правій частині цього рівняння, взаємознищуються і отже має місце формула (3). Нехай тепер X включає окрім змінних
Функція Y визначається рівністю (13), де
Теорема Донкіна доведена. Приклад 4 Центральний розтяг стержня силою Р.
можна отримати рівняння рівноваги Теорема Донкіна Якщо дві двоїстості за Юнгом функції напружень
В будівельній механіці функції потенціальної енергії пружної деформації і додатковою потенціальної енергії є позитивно визначеними квадратичними формами. Вони є двоїстими за Юнгом функціями і пов’язані між собою перетворенням Лежандра. Перетворення Лежандра є частинним випадком нерівності Юнга-Фенхеля і за фізичним змістом являє собою рівність робіт внутрішніх і зовнішніх сил, тобто відповідає теоремі Клапейрона. Екстремуми двоїстих функцій пружної деформації і додаткової енергії дають теореми Лагранжа і Кастільяно, та призводять до систем лінійних алгебраїчних рівнянь матриці яких (матриці жорсткості і матриці піддатливості) є відповідно матрицями Гессе або матрицями других похідних відповідно від потенціальної енергії пружної деформації (матриця жорсткості) і додаткової потенціальної енергії (матриця піддатливості). Вони (матриці) є позитивно визначеними і задовольняють критеріям Сильвестра, тобто усі їх головні мінори є позитивно визначені. Вони є взаємно оберненими.
Лекція 8
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 220; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.160.216 (0.036 с.) |
 опукла,
опукла,  .
. нового змінного, яка будується наступним чином:
нового змінного, яка будується наступним чином: Рис. 7.1
Рис. 7.1
 3.
3.  4.
4.  5.
5.  6.
6. 
 , які являють собою перетворення Лежандра одна до одної, називаються двоїстими за Юнгом. За визначенням перетворення Лежандра
, які являють собою перетворення Лежандра одна до одної, називаються двоїстими за Юнгом. За визначенням перетворення Лежандра 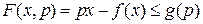 , звідки витікає нерівність Юнга
, звідки витікає нерівність Юнга .
. при перетворенні Лежандра переходить в
при перетворенні Лежандра переходить в  , то перетворення Лежандра від
, то перетворення Лежандра від  , миповинні, за визначенням, розглянути нове незалежне змінне (позначимо його через
, миповинні, за визначенням, розглянути нове незалежне змінне (позначимо його через  , скласти функцію
, скласти функцію ,
, , в якій
, в якій  має максимум:
має максимум: , тобто
, тобто  ,
,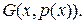
 Доведемо, що
Доведемо, що  З цього приводу відмітимо, що
З цього приводу відмітимо, що 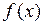 , що має нахил
, що має нахил  (див. рис. нижче). Дійсно, при фіксованому
(див. рис. нижче). Дійсно, при фіксованому  є лінійна функція від
є лінійна функція від  , і при
, і при  маємо
маємо  для визначення
для визначення  і будемо змінювати
і будемо змінювати  , що мають різний нахил
, що мають різний нахил  дорівнює
дорівнює  ), щ.м.б.д.
), щ.м.б.д. . Тоді обгинаючи має рівняння
. Тоді обгинаючи має рівняння  - перетворення Лежандра функції
- перетворення Лежандра функції  Приклад 1
Приклад 1 ,
,  ,
, 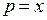 ,
, 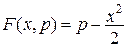 ,
, ,
,  .
. . В цьому легко пересвідчитись з рисунка. Площа трикутників
. В цьому легко пересвідчитись з рисунка. Площа трикутників
 . В усіх інших випадках
. В усіх інших випадках  , що очевидно також, якщо записати вираз
, що очевидно також, якщо записати вираз  , який завжди більше або дорівнює нулеві. Причому нулю він дорівнює при
, який завжди більше або дорівнює нулеві. Причому нулю він дорівнює при  , які пов’язані між собою перетворенням Лежандра є двоїстими за Юнгом.
, які пов’язані між собою перетворенням Лежандра є двоїстими за Юнгом. Теорема. Значення квадратичної форми
Теорема. Значення квадратичної форми 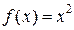 це відома властивість дотичної до параболи. Для форми
це відома властивість дотичної до параболи. Для форми  маємо
маємо  і
і  .
. .
. , щ.м.б.д.
, щ.м.б.д. (тобто квадратична форма
(тобто квадратична форма  позитивно визначена). Тоді перетворення Лежандра називається функція
позитивно визначена). Тоді перетворення Лежандра називається функція  , що визначена аналогічними попередніми рівностями
, що визначена аналогічними попередніми рівностями ,
, .
. .
. Рис. 7.5
Рис. 7.5
 Рис. 7.6
Рис. 7.6


 ,
де
,
де  – двоїсті за Юнгом функції.
– двоїсті за Юнгом функції.
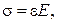


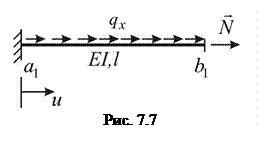 Приклад 3
Приклад 3



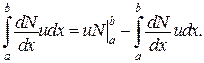

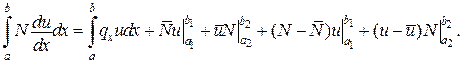
 (див. рис.)
(див. рис.)










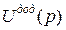



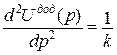
 , гесіан якої відмінний від нуля:
, гесіан якої відмінний від нуля: (1)
(1) . (2)
. (2) :
: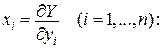 (3)
(3) . (4)
. (4) , тобто
, тобто  то Y теж включає ці параметри, тобто
то Y теж включає ці параметри, тобто  і
і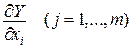 . (5)
. (5) через
через  :
: .
. виражена формулою (4), в якій змінні
виражена формулою (4), в якій змінні  замінені виразами (15). Тоді
замінені виразами (15). Тоді .
. ще і параметри
ще і параметри  .
.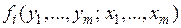 , тому
, тому
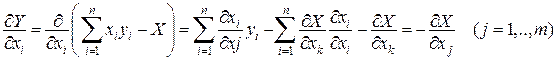 .
.
 Рис. 7.8
Рис. 7.8


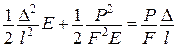


 При деформації
При деформації 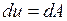 і, відповідно,
і, відповідно,
 ,
,
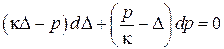
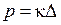 і сумісності деформацій
і сумісності деформацій 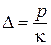 .
. ), то має місце залежність:
), то має місце залежність: