
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні припущення будівельної механікиСодержание книги
Поиск на нашем сайте
Розрахунки в будівельній механіці базуються на деяких припущеннях. Вони, як правило, збігаються з припущеннями, які мають місце в опорі матеріалів і в теорії пружності, але мають бути віднесені до всієї споруди в цілому. · Гіпотеза суцільності - тіло вважається суцільним, таким, що неперервно заповнює свій об’єм. На цій підставі деформації і переміщення точок елемента можуть вважатися неперервними функціями координат. · Гіпотеза однорідності та ізотропності: властивості матеріалу однакові в усіх точках і по усіх напрямках. · Гіпотеза ідеальної пружності: матеріал конструкцій вважається ідеально пружним. Це означає, що після зняття навантаження деформація усувається, споруда сповна поновлює форму, яку мала до початку навантаження і повертає енергію, яку було витрачено на її деформацію. · Гіпотеза лінійної залежності між деформаціями і напруженнями: вважається, щоміж напруженнями і деформаціями в усіх точках зберігається лінійна залежність (закон Гука). Завдяки цій гіпотезі, разом з попередніми, пружні властивості матеріалу в усіх точках тіла характеризуються трьома параметрами: модулем пружності E, модулем зсуву G і коефіцієнтом Пуассона n, які пов’язані між собою залежністю · Наприклад, якщо елемент AB (рис. 14.1) після деформації займає положення
Якщо переміщення малі, такі, що
то
і залежність між деформацією В опорі матеріалів при розгляді елементарної теорії згину балок гіпотеза малих переміщень дозволяє отримати точне рівняння згину балки. Загалом, у нелінійній теорії пружності доводиться, що використання лінійних виразів для компонентів деформації можливо лише за виконання двох умов: 1) подовження, зсуви і кути повороту повинні бути малі порівняно із одиницею; 2) квадратичні комбінації кутів повороту повинні бути малі порівняно з відповідними компонентами деформації. Це дає можливість суттєво спростити розрахунки споруд і вести їх за так званою недеформованою розрахунковою схемою. На рисунку, наведеному нижче, як приклад, показана деформація тонкого консольного стержня при постійному по довжині згинальному моменті за нелінійною із використанням рівняння (1.1) і лінійною («пунктир»), рівняння (1.2) теоріями. У першому випадку при сталій кривизні стержень згинається по дузі кола, у другому – по параболі. Точний розв’язок для такого стержня при умові нерозтяжності вісі, отриманий з використанням залежностей має вигляд
відповідно при Нелінійні компоненти переміщень:
З використанням розкладів тригонометричних функцій у ряди
ці розклади з урахуванням
Рис. 14.2
Загальна нелінійна теорія і розрахунки гнучких пружних стержнів викладена в [???]. Зазначимо, що оскільки залежність М і
Приклади нелінійних задач
Відносна подовжена деформація
Ураховуючи, що
Відповідно
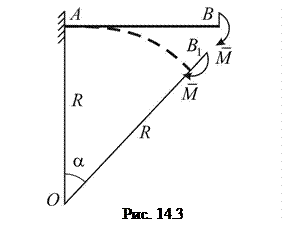
Для окремого стержня AC 1 маємо залежності:
деформації Рівність варіацій робіт внутрішніх і зовнішніх сил
дає
або, ураховуючи рівняння рівноваги Зазначимо, що задача є фізично лінійною і тому залежності
але з рис. 14.4
або
Рівність
Наприклад,
тоді
Відповідно, теореми Лагранжа і Кастільяно дають
Згідно з теоремою Донкіна, якщо
Зазначимо, що для лінійних задач, значення квадратичної форми Для форми Загалом це можна довести наступним чином. За теоремою Ейлера про однорідні функції
Тому
Координату точки 1 знаходимо із умови
Координату точки 2 знаходимо із умови
Якщо Наприклад, у випадку одновісного розтягу (рис.14.4) відповідні перетворення Лежандра мають вигляд
або, ураховуючи, що
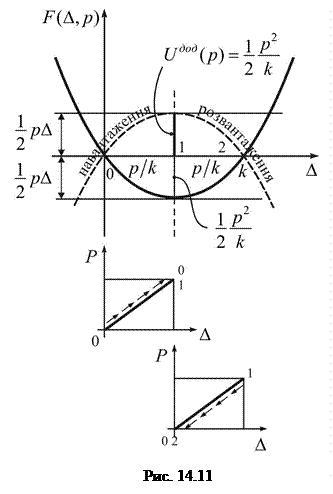
Перетворення Лежандра (рис. 14.11)
Функція Ділянка 0-1 цієї лінії відповідає навантаженню системи ( Якщо, наприклад,
де
1. 2. 3. Ураховуючи, що
послідовно отримаємо: 1. 2. 3.
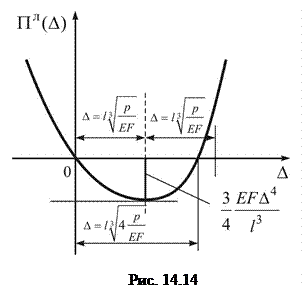
Функціонал Лагранжа задачі являє собою функцію (рис. 14.14)
екстремум якої послідовно дає
Тоді:
Справді, згідно з перетворенням Лежандра
Відповідно, теореми Лагранжа і Кастільяно дають
Згідно з теоремою Донкіна
екстремум якої дає
Рекомендована література 1. Абовский Н.П., Андреев Н.П., Деруга А.П. Вариационные принципы теории упругости и теории оболочек. - М., 1978. - 287с. 2. Александров А.В., Лащенников Б.Я., Шапошников Н.Н. Строительная механика. Тонкостенные пространственные системы. М, 1983, с. 140-237. 3. Александров А.В., Потапов В.Д. Основы теории упругости и пластичности. М, 1990, с.25-68. 4. Алексеев В.М., Тихомиров В.М., Фомин С.В. Оптимальное управление. М, 1979, с. 11-43. 5. Аппель П. Руководство теоретической (рациональной) механики, том 1. М, 1911. 6. Арнольд В.И. Математические методы классической механики. – М, Наука, 1989. 7. Бабенко А.Є., Бобир М.І., Бойко С.Л., Боронко О.О. Теорія пружності. Частина 1. – К.: «Основа», 2009. 8. Баженов В.А., Богуцкий О.А., Гоцуляк Е.А. Расчет тонких пластин, односторонне опертых по контуру. В сб. «Сопротивление материалов и теория сооружений», вып. 59, К. Будівельник, 1991, с. 3-10. 9. Баженов В.А., Гоцуляк Е.А., Богуцкий О.А. Численная реализация метода квадратичного программирования для расчета стержневых конструкций, односторонне взаимодействующих с упругим основанием. В сб. «Сопротивление материалов и теория сооружений», вып. 58, К., Будівельник, 1991, с. 3-8. 10. Баженов В.А., Гоцуляк Е.А., Кондаков Г.С., Оглобля А.И. Устойчивость и колебания деформируемых систем с односторонними связями, К. – Высшая школа, 1989. 11. Баженов В.А., Гранат СЛ., Шишов О.В. Будівельна механіка. - Київ, 1999. 584 с. 12. Баженов В.А., Дехтярюк Е.С. Будівельна механіка. Динаміка споруд. Київ, 1998, 207 с. 13. Баженов В.А., Дехтярюк Є.С. Імовірнісні методи розрахунку конструкцій. Випадкові коливання пружних систем. – К.; ВІПОЛ, 2005. 14. Баженов В.А., Іванченко Г.М., Шишов О.В. Будівельна механіка. Розрахункові вправи. Задачі. Комп’ютерне тестування. – К: Каравела, 2007. 15. Баженов В.А., Криксупов Е.З., Перельмутер А.В., Шишов О.В. Інформатика. Інформаційні технології в будівництві. Системи автоматизованого проектування. – К, Каравела, 2004. 16. Баженов В.А., Криксупов Е.З., Перельмутер А.В., Шишов О.В. Строительная информатика. Автоматизированное проектирование несущих конструкций зданий и сооружений. – М.; НАСВ, 2006. 17. Баженов В.А., Перельмутер А.В., Шишов О.В. Будівельна механіка. Комп’ютерні технології. К.; Каравела, 2009, 695с. 18. Баженов В.А., Сахаров А.С, Мельниченко Г.И., Чорный СМ. Метод конечных элементов в задачах строительной механики. - Киев, 1994. 19. Баничук Н.В. Введение в оптимизацию конструкций. М, Наука, 1986, 298с. 20. Безухов Н.И. Примеры и задачи по теории упругости, пластичности и ползучести. М.: Госстройиздат, 1965. 21. Безухов Н.И. Примеры и задачи по теории упругости, пластичности и ползучести. – М.:, 1965. 22. Безухов Н.И., Лужин О.В. Приложение методов теории упругости и пластичности к решению инженерных задач. М., Высшая школа, 1974. 23. Беленький И.М. Введение в аналитическую механику. М, 1964. 24. Бердичевский В.Л. Вариационные принципы механики сплошной среды. М., Наука, 1983. 25. Бернштейн М.С. Расчет конструкций с односторонними связями, Стройиздат 1947. 26. Бернштейн С.А. Очерки по истории строительной механики. – М; ГИЛСА, 1957. 27. Бляшке В. Круг и шар. – М.: Наука, 1967. – 232 с. 28. Боголюбов А.Н. Математики Механики. Киев, Наукова думка, 1983, 638с, 29. Босаков С.В. Метод Ритца в примерах и задачах по строительной механике и теории упругости. Учебное пособие, Минск 2000, 142с. 30. Варвак П.М. и др. Метод конечных элементов. К, с. 4-38, 1981. 31. Варвак П.М. Новые методы решения задач сопротивления материалов. К, 1977, с.122-153. 32. Варвак П.М., Варвак Л.П. Метод сеток в задачах расчета строительных конструкций. М, 1977. 33. Васидзу К. Вариационные методы в теории упругости и пластичности. М., Мир, 1987. 34. Гантмахер Ф.Р. Лекции по аналитической механике. М, 1966, с. 11-34. 35. Гантмахер Ф.Р. Теория матриц. М, 1967, с.225-227. 36. Гельфанд Н.М., Фомин С.В. Вариационное исчисление. М, 1961г. 37. Гловинский Р., Лионс Ж.-Л., Тремольер Р. Численное исследование вариационных неравенств. М., Мир, 1979, 562с. 38. Гольденблат И.И. Экстремальные и вариационные принципы в теории сооружений "Строительная механика в СССР" (1917-1957). М., Гостехиздат, 1957. 39. Гордеев В.Н. Перельмутер А.В. Расчет упругих схем с односторонними связями, как задача квадратического программирования – В кн. Исследования по теории сооружений, вып. X V.M, Стройиздат, 1967. 40. Гуляев В.И., Баженов В.А., Попов С.Л. Прикладные задачи теории нелинейных колебаний механических систем. М, Высшая школа, 1989. 41. Дюво Г., Лионс Ж.-Л. Неравенства в механике и физике. М., Наука, 1980, 382с. 42. Жозеф Луи Лагранж. Сборник статей к 200-летию со дня рождения. Изд. АНСССР. М-Л; 1937. 43. Ильин В.П., Карпов В.В., Масленников A.M. Численные методы решения задач строительной механики. Минск, 1990, с. 181-207. 44. Ильюшин А.А. Пластичность. – М.: Изд-во АН СССР, 1963. 45. Исаханов Г.В., Гранат С.Я., Мельниченко Г.И., Шишов О.В. Строительная механика. Расчет стержневых систем на ЭВМ. К, 1990 г. 46. Канторович Л.В. и Крылов В.И. Приближенные методы высшего анализа. М-Л, 1962, с. 258-323. 47. Каудерер Т. Нелинейная механика, - М, 1961. 48. Качанов Л.М. Основы теории пластичности. - М.: Наука, 1969. 49. Кирпичев В.Л. Беседы о механике. ГИТТЛ, М, Л., 1951, 360 с. 50. Клаф Р., Пензиен Дж. Димика сооружений. – М., Мир, 1965. 51. Клаф Р., Пензиен Дж. Динамика сооружений. М, 1979 с. 14-20, с.231-244. 52. Колтунов М.А. Прикладная механика деформируемого твердого тела. 53. Корн Г. и Корн Т. Справочник по математике. Изд. «Наука», М, 1970, с.318-329. 54. Курант Р., Гильберт Д. Методы математической физики. Т.1 - М., 1951.-476с. 55. Курант Р., Гильберт Д. Методы математической физики. Т.2 - ОГИЗ, Гостехиздат, 1945. - 619с. 56. Лаврентьев М.и Люстерник Л. Основы вариационного исчисления, том первый, ч. П., ОНТИ, НКТП, 1935, М, Л. 399 с. 57. Лазарян В.А. Энергия деформации и перемещения линейных систем. К., Наукова думка, 1972, 139 с. 58. Ландау Л.Д., Лившиц Е.М. Теория упругости. - М.: Наука, 1987. 59. Ланцош К. Вариационные принципы механики. М, 1965, с.57-96. 60. Лейбензон Л.С. Курс теории упругости. М. Л, 1947, с.306-328. 61. Лурье А.И. Нелинейная теория упругости, М., Наука, 1980. 62. Малинин Н.Н. Прикладная теория пластичности и ползучести. - М.: Машиностроение, 1975. 63. Михлин С.Г. Вариационные методы в математической физике. М. 1970, с. 118-120, с. 160-190. 64. Михлин С.Г. Прямые методы математической физики. 65. Михлин С.Г. Численная реализация вариационных методов. М. 1966. 66. Можаровський М.С. Теорія пружності, пластичності і повзучості. – К.: «Вища школа», 2002. 67. Мышкис А.А. Математика для втузов. Специальные курсы. Изд. «Наука», М, 1971, с.257-384. 68. Новожилов В.В. Теория тонких оболочек, Оборонгиз 1941. Судпромгиз 1951. 69. Новожилов В.В. Теория упругости. Судпром, ГИЗ, 1958, 365 с. 70. Образцов И.Ф., Савельев Л.М., Хазанов Х.С. Метод конечных элементов в задачах строительной механики летательных аппаратов. М. 1985, с. 27-46. 71. Панагиогопулос П. Неравенства в механике и их приложения. Выпуклые и невыпуклые функции энергии. М, Мир, 1989, 492 с. 72. Папкович П.Ф. Теория упругости. Л., Оборонгиз, 1939, 640 с. 73. Перельмутер А.В. Исследование метода квадратного программирования для расчета схем с односторонними связями, - В кн. «Исследования по теории сооружений», вып. XIX. M, Стройиздат, 1972. 74. Перельмутер А.В. К вопросу о кинематическом анализе ссистем, содержащих односторонние связи, - «Строительная механика и расчет сооружений», 1970, №1. 75. Перельмутер А.В. Статические и кинематические свойства систем с односторонними связями – «Строительная механика и расчет сооружений», 1968, №2. 76. Перельмутер А.В., Сливкер В.И. Расчётные модели сооружений и возможность их анализа. 3-е изд. – М, ДМК Пресс, 2007 – 600 с. 77. Перельмутер А.В., Сливкер В.И. Устойчивость равновесия конструкций и родственные проблемы. Т. 1. – М; изд. СКАД СОФТ, 2007. 78. Піскунов В.Г. та інші. Опір матеріалів з основами теорії пружності й пластичності. Київ, Вища школа, книга 1, 1994р., - 201с, книга 2, 1994 - 335с, книга 3, 1995 - 271с, книга 4, 1995 - 303с, книга 5, 1995 - 207с. 79. Подгорный А.Н., Марченко Г.А., Пустынников В.И. Основы и методы прикладной теории упругости. М. 1981, с.264-287. 80. Попов Е.П. Теория и расчёт гибких упругих стержней. – М. Наука, 1986. 81. Потапов В.Д., Александров А.В., Косицин С.Б., Долотказин Д.Б. Строительная механика: в 2 кн. Кн. 1. Статика упругих систем. – М, Высшая школа, 2007. 82. Пратусевич Я.А. Вариационные методы в строительной механике. М-Л. 1948, с. 10-28. 83. Прудников А.П., Бричко Ю.И., Маричев О.И. Интегралы и ряды. Элементарные функции. М., Наука, 1981. 84. Рабинович И.М. Вопросы теории сталитического расчета сооружений с односторонними связями, М, Стройиздат, 1975. 85. Ректорис К. Вариационные методы в математической физике и технике. М., Мир, 1985,с.185-313. 86. Ржаницын А.Р. Строительная механика. М., Высшая школа, 1982, 400 с. 87. Розин Л.А. Вариационные постановки задач для упругих систем. Л, 1978, с.8-32. 88. Розин Л.А. Задачи теории упругости и численные методы их решения. Санкт-Петербург, изд. СПбГТУ, 1998, 530 с. 89. Розин Л.А. Теоремы и методы статики деформируемых систем. Л, 1986, с.9-34. 90. Рыбаков Л.С., Наринский В.И. Вариационные принципы и методы строительной механики. М.: МАИ, 1987. 91. Сливкер В.И. Строительная механика. Вариационные основы. М. 2005., 708 с. 92. Смирнов А.Ф., Александров А.В., Лащенников Б.Д., Шапошников Н.Н. Строительная механика. Стержневые системы. М. 1981, с.279-308. 93. Смирнов А.Ф., Александров А.В., Лащенников Б.Я., Шапошников Н.Н. Строительная механика. Динамика и устойчивость сооружений. М, 1984. 94. Справочник по теории упругости под. Ред. П.М. Варвака и А.Ф. Рябова. - Киев, 1971, с.206-212. 95. Тимошенко С.П. История науки о сопротивлении материалов. – М., ГИТТЛ, 1957. 96. Тимошенко С.П. Сборник задач по сопротивлению материалов. М. Л.: 1928. 97. Тимошенко С.П. Сопротивление материалов, т.1. М, Госрехиздат, 1945. 98. Тимошенко С.П. Сопротивление материалов. В 2 ч. 4.2. Теория и задачи. М. Л.: Гостехтеориздат, 1932. 99. Тимошенко С.П. Статические и динамические проблемы теории упругости. К.: Наукова думка, 1975. 100. Тимошенко С.П. Устойчивость стержнем, пластин и оболочек. М.: Наука, 1971. 101. Тимошенко С.П., Войновский–Критер С. Пластинки и оболочки. – М, Наука, 1966. 102. Тюлина И.А. Жозеф Луи Лагранж. Изд. «Наука», М, 1977, 221 с. 103. Феодосьев В.И. Избранные задачи и вопросы по сопротивлению материалов. – М; Наука, 1967. 104. Фикера Г. Теоремы существования в теории упругости, 1974. 105. Филин А.П. Матрицы в статике стержневых систем. Л.М, 1966, с. 107-116. 106. Филин А.П. Прикладная механика твердого деформируемого тела. т.II, М.Л. 1978, с.438-531., т.1 1975г. т.Ш, 1981г. 107. Фомин С.В. Оптимальное управление. М, «Наука», 1979., 429 с. 108. Химмельблау Д. Прикладное нелинейное программирование. – М, Мир, 1975. 109. Цлаф Л.Я. Вариационное исчисление и интегральные уравнения. Москва. ГИФМЛ, 1970, 184с. 110. Чирас А.А. Строительная механика. М, 1989, с.58-68. 111. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление, изд. Наука, М. 1965, с.281-413. 112. Янг Л. Лекции по вариационному исчислению и теории оптимального управления. Изд. «Мир», М., 1974, 488с. 113. Lagrange. Mecanique analitike, Paris, 1788.
[1] Важко сказати, коли вперше була висловлена думка про найбільшу «місткість» кола і сфери серед всіх замкнених кривих однакової довжини, або поверхонь однакової площі. Один з останніх учнів афінської школи платоніків Симпліций (VI ст. н. е.), що склав незадовго до остаточного краху античної цивілізації великий коментар до праць Арістотеля (IV ст. до н. е.), пише: «Доведено до Арістотеля, бо він користується цим, як відомим, а потім більш повно – Архімедом і Зенодором, що серед ізопериметричних фігур найбільш містким є коло, а серед ізопіфанних – куля». У цих словах визначена постановка таких екстремальних задач: серед плоских замкнених кривих, що мають задану довжину, знайти криву, яка охоплює найбільшу площу, і серед просторових замкнених поверхонь, що мають задану площу, знайти поверхню, яка охоплює найбільший об'єм. Для філософа-платоніка така постановка задачі є природною і пов'язана з пошуком ідеальних форм. Недаремно коло і куля були в давнину символами геометричної досконалості. [2] Прозаїчніше мотивування ізопериметричної і близьких до неї задач можна знайти в дещо наївній, але достатньо виразній формі в легенді про Дідону. Нагадаємо її за «Енеїдою» римського поета Вергілія. Фінікійська царівна Дідона із невеликим загоном жителів міста Тіра, рятуючись від переслідувань тирана – брата Дідони, покинули рідне місто і відправилися на кораблях на захід вждовж берегів Середземного моря. Вибравши на африканському узбережжі зручне місце (нинішня Туніська затока), Дідона і її супутники вирішили заснувати тут поселення. Мабуть, ця ідея не сподобалася місцевим жителям, але Дідоні вдалося умовити їх предводителя Ярба, і він необережно погодився поступитися клаптиком землі, «який можна оточити бичачою шкурою». Ярб не відразу зрозумів хитрість і підступність фінікіянки. Розрізавши шкуру на тонкі смужки, Дідона зв'язала їх в один довгий ремінь і, оточивши їм значну територію, заклала на ній місто Карфаген (фінікійське Картадашт – нове місто). На згадку про цю історію цитадель Карфагена дістала назву Бірса (мовою пунійців, так римляни називали жителів Карфагена, – шкура). Цією назвою послуговуються і досьогодні. Всі ці події легенда відносить до 825 (або до 814) р. до н.е. У такій ситуації виникає та ж сама класична ізопериметрична задача: вказати оптимальну форму ділянки землі, яка при заданій довжині периметра L має найбільшу площу S. Її розв’язком є коло. Інші постановки задачі можна отримати якщо, як це природно припустити, Дідона хотіла зберегти вихід до моря. На відміну від класичної ізопериметричної задачі, ці задачі будемо називати задачами Дідони. [3] Перший загальний аналітичний прийом розв’язання екстремальних задач розроблений П’єром Ферма. Відкритий він, мабуть, у 1629 р., але вперше достатньо повно викладений в листі до Роберваля у 1638р. Щоб осягнути первинну думку Ферма можна звернутися до книги Декарта, де цей лист наведений. (Р. Декарт. Геометрія. З додатком вибраних робіт П. Ферма і листування Декарта. − М. − Л.: ГОНТІ, 1938, с. 154). Сучасною мовою (правда, у Ферма лише для поліномів) прийом Ферма зводиться до того, що при знаходженні екстремуму функції без обмежень в точці екстремуму має виконуватися рівність. Відомо, що перший натяк на цей результат з’явився в словах Кеплера із «Стереометрії винних бочок». Точного сенсу міркування Ферма набули через 46 років, коли у 1684 р. з'явилася робота Лейбніца, в якій закладалися основи математичного аналізу. Вже сам заголовок цієї роботи, який починається так: «Nova methodus pro maximis et minimis...» («Новий метод знаходження найбільших і найменших значень...»), свідчить про важливість задачі знаходження екстремумів в становленні сучасної математики. У своїй статті Лейбніц не тільки отримує як необхідну умову співвідношення (цей результат зараз називають теоремою Ферма),але і використовує другий диференціал для розрізнення максимуму і мінімуму. Слід зазначити, що більшість наведених Лейбніцем фактів на той час були відомі також і Ньютону. Проте його робота «Метод флюксій», завершена в основному до 1671 р., була опублікована тільки у 1736 р.
[4] Лагранж Жозеф Луі (фр. Joseph Louis Lagrange, італ. Giuseppe Lodovico Lagrangia; 1736 - 1813) — французський математик, астроном і механік італійського походження. Народився в Турині. Вчився у Туринському університеті. Дослідження присвячені механіці, геометрії, теорії диференціальних рівнянь, математичному аналізу, алгебрі, теорії чисел та іншим розділам математики, а також теоретичній астрономії. В роботі „Аналітична механіка” (1788) Лагранж підвів підсумок усьому, що було зробленоу механіці протягом XVIII ст. і завершив математизацію механіки. В основу статики він поклав принцип можливих переміщень, а в основу динаміки – поєднання принципу можливих переміщень з принципом Д’Аламбера. У роботах „Теорія аналітичних функцій” (1797) і „Лекції по численню функцій” (1801) зробив спробу обгрунтувати аналіз, зводячи його до алгебри. Запропонував аналітичне викладення варіаційного числення. Виходячи із результатів Л.Ейлера розробив основні поняття варіаційного числення. Ввів потрійні інтеграли. В теорії аналітичних функцій побудував ряд, що носить його ім’я і довів декілька теорем, сформульованих П.Ферма. В механіці і математиці Лагранж виконав роботу з систематизації отриманих результатів і їх обгрунтуванню.
[5] Дю-Буа-Реймонд, Поль Давид Густав (нім. Paul David Gustav du Bois-Reymond, 1831–1889) – німецький математик. Його ім'ям названа одна з лем варіаційного числення.
[6] Пуассон, Сімеон Дені (фр. Siméon-Denis Poisson, 1781 — 1840) – французький математик, механік і фізик, один із засновників математичної фізики. Дослідження присвячені варіаційному численню, теорії ймовірності, математичній фізиці, механіці, зокрема, теорії пружності, опору матеріалів. Написав «Курс механіки» (1811), який багато разів перевидавався.
[7] В цьому функціоналі знак змінений на зворотній порівняно з традиційною формою функціонала Кастільяно з тим, щоб витримати принцип двоїстості за Юнгом у нерівності Лежандра. Тобто прийнято, що відповідні значення функціоналів і будуть співпадать, оскільки вони є квадратичними формами.
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 237; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.69.101 (0.018 с.) |

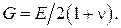
 Гіпотеза малих переміщень: переміщення точок системи, які зумовлені пружними деформаціями, є малими, тобто такими, що допускають лінійну залежність між деформаціями і переміщеннями в рівняннях геометричного аспекту задачі, а також складання рівнянь рівноваги для недеформованого стану.
Гіпотеза малих переміщень: переміщення точок системи, які зумовлені пружними деформаціями, є малими, тобто такими, що допускають лінійну залежність між деформаціями і переміщеннями в рівняннях геометричного аспекту задачі, а також складання рівнянь рівноваги для недеформованого стану. , то лінійна деформація
, то лінійна деформація  може бути обчислена в такий спосіб:
може бути обчислена в такий спосіб: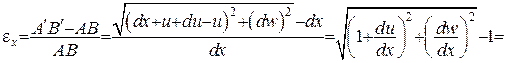

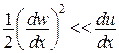 ,
,
 і переміщенням u є лінійною.
і переміщенням u є лінійною.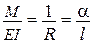 ,
,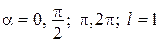 .
.
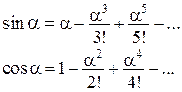
 можуть бути спрощені, а саме
можуть бути спрощені, а саме і
і  .
.
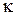 є лінійною (
є лінійною (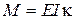 ), то, як і вище, можна отримати варіаційні постановки і для задачі.
), то, як і вище, можна отримати варіаційні постановки і для задачі.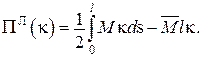 Додаткові умови:
Додаткові умови:

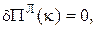
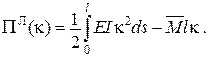
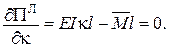
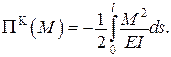 Додаткові умови:
Додаткові умови:
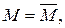
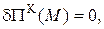
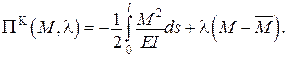
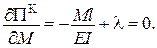
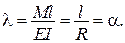
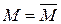
 .
.
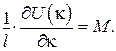
 .
.

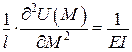 .
.
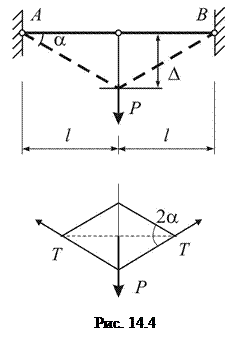 Розглянемо задачу, наведену у [???], яка тлумачиться як «виключний випадок» у тому розумінні, що теорема Кастільяно не дає належного результату, коли переміщення не пропорційні силам. Проте автор при застосуванні теореми Кастільяно не використовує поняття додаткової потенціальної енергії, а помилково користується величиною потенціальної енергії пружної деформації, вираженою через сили.
Розглянемо задачу, наведену у [???], яка тлумачиться як «виключний випадок» у тому розумінні, що теорема Кастільяно не дає належного результату, коли переміщення не пропорційні силам. Проте автор при застосуванні теореми Кастільяно не використовує поняття додаткової потенціальної енергії, а помилково користується величиною потенціальної енергії пружної деформації, вираженою через сили. дорівнює
дорівнює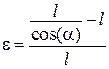 .
.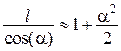 ,
, 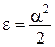 .
. .
.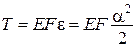 ;
; 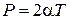 ,
,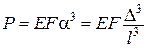 ;
;  ,
,  .
. переміщення
переміщення  ,
,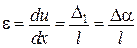 ,
, 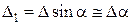 .
.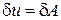
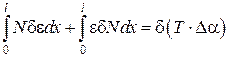 ,
,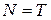 .
.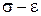 і, відповідно,
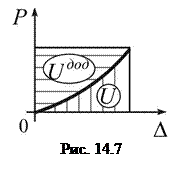
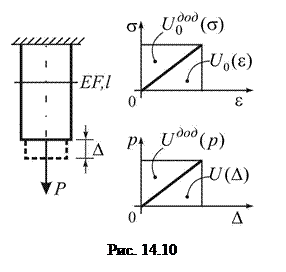
і, відповідно, 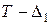 є лінійними (рис. 14.6).
є лінійними (рис. 14.6). ,
,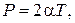




 ,
,
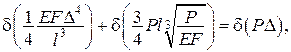
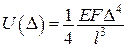 ;
; 

 ;
; 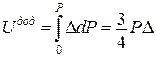 .
.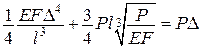 (♦)
(♦)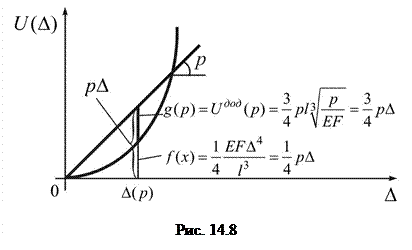 є перетворенням Лежандра, а функції
є перетворенням Лежандра, а функції 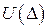 і
і 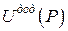 є двоїстими за Юнгом (рис. 14.8).
є двоїстими за Юнгом (рис. 14.8). ,
,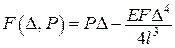 ,
, ,
, ,
, .
. ;
; 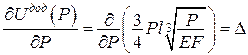 .
.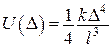 , а
, а 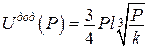 ,
, 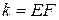
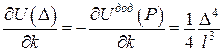 .
. і її перетворення Лежандра
і її перетворення Лежандра  у відповідних точках співпадають
у відповідних точках співпадають 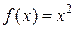 це являє собою відому властивість дотичної до параболи.
це являє собою відому властивість дотичної до параболи. .
.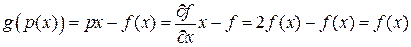 .
. Причому
Причому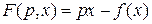 ,
, ,
, .
. ;
; 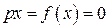 ;
;  ;
; .
.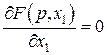 ;
;  ;
;  ;
;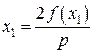 .
.
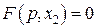 ;
;  ;
; 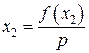 .
.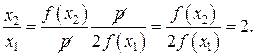
 є вісь симетрії.
є вісь симетрії. ;
; 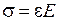
 ,
,  - двоїсті за Юнгом функції.
- двоїсті за Юнгом функції. ,
,
 ;
; 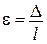 ,
,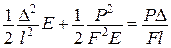 ,
, ,
,  ,
,  ,
,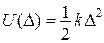 і
і 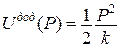 - двоїсті за Юнгом функції, які являють відповідно потенціальну енергію пружної деформації і додаткову потенціальну енергію.
- двоїсті за Юнгом функції, які являють відповідно потенціальну енергію пружної деформації і додаткову потенціальну енергію. ,
,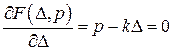 ;
;  ,
,
 .
.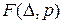 являє собою функціонал Лагранжа
являє собою функціонал Лагранжа 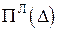 , або повну потенціальну енергію системи (із зворотнім знаком), на графіку
, або повну потенціальну енергію системи (із зворотнім знаком), на графіку 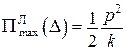 – додаткова потенціальна енергія або робота внутрішніх сил), а ділянка 1-2 – розвантаженню, тобто приведенню системи у первісний стан. Вісь О–О
– додаткова потенціальна енергія або робота внутрішніх сил), а ділянка 1-2 – розвантаженню, тобто приведенню системи у первісний стан. Вісь О–О  ; яка є умовою перетворення Лежандра, є віссю симетрії. У загальному випадку це має місце для так званих лінійних систем, двоїсті функції яких рівні і???.
; яка є умовою перетворення Лежандра, є віссю симетрії. У загальному випадку це має місце для так званих лінійних систем, двоїсті функції яких рівні і???. (рис. 14.12), то можна отримати
(рис. 14.12), то можна отримати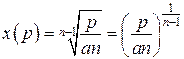 ,
, ,
, – координата екстремуму, а
– координата екстремуму, а  – координата середини.
– координата середини.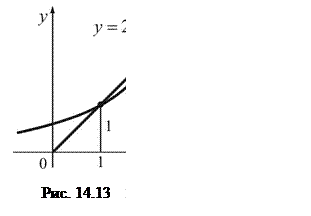 Порівнюючи ці залежності, тобто криві
Порівнюючи ці залежності, тобто криві 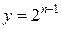 і
і  (рис. 14.13), можна отримати:
(рис. 14.13), можна отримати: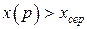 , якщо
, якщо 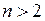 ;
; , якщо
, якщо  ;
; , якщо
, якщо 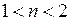 .
. ,
, , якщо
, якщо 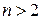 ;
;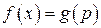 , якщо
, якщо 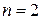 ;
; , якщо
, якщо 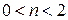 .
. Проілюструємо ці положення на подальших прикладах нелінійних задач.
Проілюструємо ці положення на подальших прикладах нелінійних задач.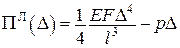 ,
,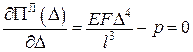 ;
;  ;
; 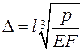 ,
,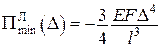 .
.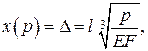


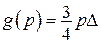 ;
; 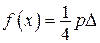 .
. Зазначимо, що у випадку нелінійної задачі крива
Зазначимо, що у випадку нелінійної задачі крива  не є симетричною відносно вісі
не є симетричною відносно вісі  (рис. 14.15). Наприклад, зменшення вдвічі
(рис. 14.15). Наприклад, зменшення вдвічі 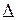 вимагає відповідне зменшення
вимагає відповідне зменшення  у 8 разів.
у 8 разів. Як приклад, розглянемо наступну нелінійну задачу [Варвак], де задана залежність
Як приклад, розглянемо наступну нелінійну задачу [Варвак], де задана залежність 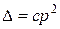 , яка має опуклість, протилежну порівняно із розглянутою вище (рис. 14.16). Необхідно побудувати перетворення Лежандра і функціонал Лагранжа.
, яка має опуклість, протилежну порівняно із розглянутою вище (рис. 14.16). Необхідно побудувати перетворення Лежандра і функціонал Лагранжа.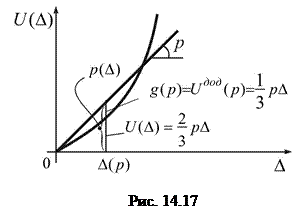
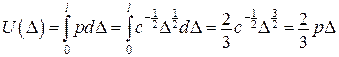 ,
,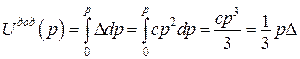 ,
,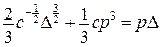 (рис. 14.17).
(рис. 14.17).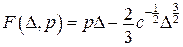 ,
,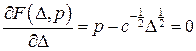 ,
,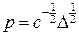 ,
, 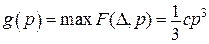 .
.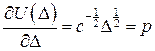 ;
; 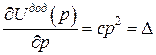 .
. .
.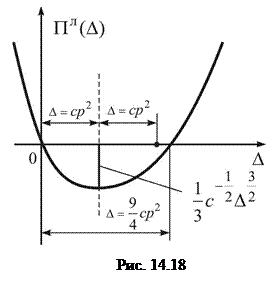 Функціонал Лагранжа задачі являє собою функцію (рис. 14.18)
Функціонал Лагранжа задачі являє собою функцію (рис. 14.18)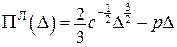 ,
,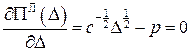 ;
;  ;
;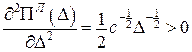 – мінімум,
– мінімум, ;
;  ;
;  .
. і
і  ,
,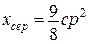 ,
,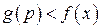 ,
, ,
, 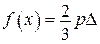 .
. Тобто, у даному випадку нелінійної задачі крива
Тобто, у даному випадку нелінійної задачі крива 


