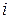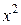Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні поняття варіаційного числення. Функціонал і варіація. Типи задач варіаційного числення. Абсолютний і умовний екстремум. Екстремум функції і екстремум функціоналуСтр 1 из 7Следующая ⇒ Конспект лекцій з курсу „Варіаційні основи будівельної механіки” Київ-2011 ЗМІСТ
Лекція 1. (2 пари) Приклад 1
Тобто екстремалями є прямі лінії, які визначають найкоротшу відстань між точками Приклад 2 Знайти екстремум функціонала
Граничні умови
Рівняння Ейлера
Таким чином екстремум функціоналу досягається на прямій Приклад 3 Задача про брахістохрону: визначити криву, що з’єднує задані точки А і В, по якій матеріальна точка переміститься із А у В за найкоротший час (тертям і опором середовища нехтуємо). Розмістимо початок координат в точці А, вісь
Оскільки цей функціонал належить до найпростішого виду і його підінтегральна функція не містить явно
Після спрощень матимемо
Отже, в параметричній формі рівняння шуканої лінії має вигляд
Змінюючи параметр за допомогою підстановки
де Функціонали, які залежать від другої похідної. Рівняння Ейлера-Пуассона [6]
Функціонал
Варіаційне рівняння для цього функціонала має вигляд:
або
З урахуванням позначень частинних похідних
отримаємо
До другого і третього членів цього рівняння застосуємо процедуру перетворення по частинах
Аналогічно
Підсумовуючи підкреслені члени отримаємо:
Згідно з лемою Лежандра отримаємо
– рівняння Ейлера-Пуассона для функціоналу, який залежить від другої похідної. Граничні умови
По аналогії запишемо рівняння Ейлера-Пуассона для функціоналу, який залежить від n-ї похідної
Рівняння Ейлера-Пуассона мають порядок 2 n.
Граничні умови
Приклад 4
Граничні умови
Рівняння Ейлера-Пуассона
Диференціальне рівняння Ейлера Загальний розв’язок:
Реалізуємо граничні умови 1) 2) 3) 4)
Приклад 6
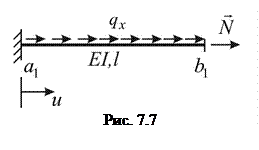
Надалі буде показано, що вихідний функціонал Лекція 3 Основні залежності механіки стержнів.Рівняння статичної, геометричної і фізичної сторін задачі для стержня 1. Статична сторона задачі. Рівняння рівноваги Розглянемо нескінченно малий елемент стержня.
Рис. 3.1 Інтегральні характеристики
Приріст кожного із зусиль визначається так:
Отримаємо рівняння рівноваги у вигляді: 1. 2. 3. 2. Геометрична сторона задачі. Зв'язок між деформаціями і переміщеннями
Приклад
3. Фізична сторона задачі. Закон Гука
де G – модуль зсуву, Е – модуль пружності (модуль Юнга).
де µ- коефіцієнт Пуассона (залежність між поперечними і повздовжніми деформаціями), µ=0…0,5. Найпростіший напружений стан – розтяг-стиснення (див. рис. 3.4)
Розрахував коефіцієнт k Томас Юнг в 1807 р.
Кулон у 1784 році отримав при скрученні стержня залежність
А.Навьє в 1826 році ввів поняття напруження і отримав
тобто через 150 років після оприлюднення закону Гука. Далі Коші ввів поняття про головні напруження
а Пуассон ввів коефіцієнт Тобто, до фундаментальних понять про напруження і деформації людство йшло майже два століття, хоч впритул до цього наблизився Юнг і навіть близько був ще Галілей.
* Цікавою є історія становлення закону Гука. Знаний англійський учений Роберт Гук в 1660 р. сформулював, а в 1676 р. оприлюднив, і то у вигляді анаграми, таке: «яка деформація, таке і навантаження» (навіть не навпаки). Майже одночсасно з Гуком (1680 р.) і незалежно від нього цей закон сформулював француз Маріотт: «навіть найбільш тверді тіла – скло і залізо – деформуються пропорційно навантаженню». Тобто, Деформація Постановка крайової задачі механіки стержнів у зусиллях і переміщеннях. Розглянемо балку.
Граничні умови
а індексами «2», відповідно, точки, у я ких задані кінематичні характеристики
Рівняння (*) можна звести до одного рівняння і отримати постановку крайової задачі механіки стержнів у переміщеннях
При цьому
Тоді граничні умови
Лекція 4 Лекція 5 Лекція 7 Приклад 2 Для форми Доведення. З теореми Ейлера про однорідні функції
Отже, Випадок багатьох змінних. Нехай тепер
Усі попередні міркування, в тому числі нерівність Юнга, без змін переносяться на цей випадок. Отже, функції Аналогічні висновки можна зробити і при нелінійній залежності
Робота зовнішніх сил
При цьому
Основна інтегральна формула (формула Гріна):
Тоді отримаємо
відомий вираз для теореми Клапейрона.
При
При
Функції потенціальної енергії пружної деформації
Другі похідні від потенціальної енергії пружної деформації по переміщенню і від додаткової потенціальної енергії по відповідній дорівнюють відповідно коефіцієнтам матриці жорсткості та матриці піддатливості. Теорема Донкіна Нехай задана деяка функція
і нехай існує перетворення змінних, викликане функцією
Тоді існує перетворення, зворотне до перетворення (2), яке теж породжено деякою функцією
при цьому функція Y, що породжує функцію зворотного перетворення, пов’язана з функцією Х, що породжує пряме перетворення, формулою:
Якщо функція включає параметри
Доведення. Гесіан функції X співпадає з якобіаном правих частин у рівнянні (2). Тому умова (1) показує, що з рівняння (2) показати змінні
Нехай функція
Але згідно рівняння (2), два доданки, які знаходяться в правій частині цього рівняння, взаємознищуються і отже має місце формула (3). Нехай тепер X включає окрім змінних
Функція Y визначається рівністю (13), де
Теорема Донкіна доведена. Приклад 4 Центральний розтяг стержня силою Р.
можна отримати рівняння рівноваги Теорема Донкіна Якщо дві двоїстості за Юнгом функції напружень
В будівельній механіці функції потенціальної енергії пружної деформації і додатковою потенціальної енергії є позитивно визначеними квадратичними формами. Вони є двоїстими за Юнгом функціями і пов’язані між собою перетворенням Лежандра. Перетворення Лежандра є частинним випадком нерівності Юнга-Фенхеля і за фізичним змістом являє собою рівність робіт внутрішніх і зовнішніх сил, тобто відповідає теоремі Клапейрона. Екстремуми двоїстих функцій пружної деформації і додаткової енергії дають теореми Лагранжа і Кастільяно, та призводять до систем лінійних алгебраїчних рівнянь матриці яких (матриці жорсткості і матриці піддатливості) є відповідно матрицями Гессе або матрицями других похідних відповідно від потенціальної енергії пружної деформації (матриця жорсткості) і додаткової потенціальної енергії (матриця піддатливості). Вони (матриці) є позитивно визначеними і задовольняють критеріям Сильвестра, тобто усі їх головні мінори є позитивно визначені. Вони є взаємно оберненими.
Лекція 8 Перетворення Лежандра
Принцип Лагранжа-Дирихле Для консервативної системи стійка, нестійка, байдужа рівновага мають місце відповідно:
Теорема Клапейрона
Відповідні екстремальні значення функціоналів Лагранжа і Кастільяно співпадають. Варіаційні рівняння функціоналів Лагранжа і Кастільяно утворюють так звану пару двоїстих задач варіаційного числення, коли попередні умови однієї задачі є природними умовами іншої і навпаки. Під природними умовами розуміються умови, яким задовольняють відповідні варіаційні рівняння. За допомогою методу множників Лагранжа можна “поміняти місцями” додаткові і природні умови, тобто із функціонала Лагранжа отримати функціонал Кастільяно і навпаки. Таке перетворення у варіаційному численні має назву перетворення Фрідріхса. Зазначимо, що екстремальні значення функціоналів Лагранжа і Кастільяно, а також усіх функціоналів, які отримані за допомогою множників Лагранжа співпадають. Лекція 9 Лекція 10 Приклад Задаємо w у вигляді ряду:
Запишемо їх у вигляді таблиці:
Обчислимо відповідні коефіцієнти матриці алгебраїчних рівнянь (матриці жорстк
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 360; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.132.200 (0.003 с.) |
 ,
,
 ,
,

 Рис. 2.2
Рис. 2.2


 і
і  .
. .
.

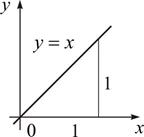 Рис. 2.3
Рис. 2.3
 дає розвязок:
дає розвязок: 
 . Причому
. Причому  на всьому відрізку [0,1].
на всьому відрізку [0,1]. спрямуємо горизонтально, вісь
спрямуємо горизонтально, вісь  − вертикально донизу. Швидкість руху матеріальної точки
− вертикально донизу. Швидкість руху матеріальної точки  . Час, що витрачається на переміщення точки з положення
. Час, що витрачається на переміщення точки з положення  в положення
в положення 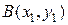 , визначається за формулою
, визначається за формулою ,
,  ,
,  .
. , або в даному випадку
, або в даному випадку .
. або
або  . Введемо параметр
. Введемо параметр  , вважаючи
, вважаючи  , і дістанемо
, і дістанемо ;
;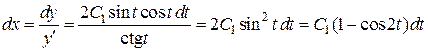 ;
; .
. ,
,  .
. і враховуючи, що
і враховуючи, що  , оскільки при
, оскільки при  маємо
маємо  , дістанемо рівняння сімейства циклоїд у звичайній формі:
, дістанемо рівняння сімейства циклоїд у звичайній формі: ,
,  ,
, − радіус круга, що котиться. Радіус визначається з умови проходження циклоїди через точку
− радіус круга, що котиться. Радіус визначається з умови проходження циклоїди через точку  .
. ,
, .
.
 .
. ,
,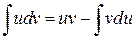 ,
,

 ,
,  ,
,  .
.

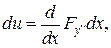

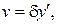

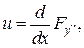



 .
.
 ,
,  ,
,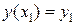 ,
,  .
. .
. .
.



 .
. ,
,
 ,
,
 .
.

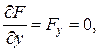


 є рівняння 4 порядку.
є рівняння 4 порядку.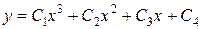 ,
, .
. ,
, ,
,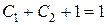
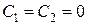 ,
,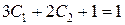
 .
Тобто функціонал досягає екстремуму на прямій
.
Тобто функціонал досягає екстремуму на прямій 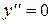 на всьому відрізку [0,1] (див. рис.).
на всьому відрізку [0,1] (див. рис.).
 Рис. 2.4
Рис. 2.4
 Рис. 2.5
Рис. 2.5



 .
Екстремаль
.
Екстремаль  . Причому
. Причому  ,
,  Рис. 2.6
Рис. 2.6
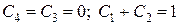 ,
,
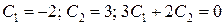 .
Екстремаль
.
Екстремаль
 ,
,
 ,
,
 ,
Точка перетину
,
Точка перетину
 ;
;  ,
,
 ;
;  (див. рис.).
(див. рис.).
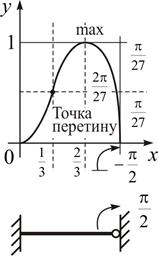 Рис. 2.7
Рис. 2.7


 .
.
 Екстремаль
Екстремаль
 ,
,
 (екстремум),
(екстремум),
 (точка перетину).
Точка перетину
(точка перетину).
Точка перетину
 ;
;  ;
;  Рис. 2.8
Рис. 2.8

 .
Екстремаль
.
Екстремаль
 ,
,
 .
Екстремум при
.
Екстремум при 
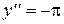
 .
.
 Рис. 2.9
Рис. 2.9

 .
Екстремаль
.
Екстремаль
 ;
;  .
.
 ;
; 


 ,
,  ,
,  .
. .
.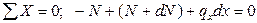






 Рис. 3.2
Рис. 3.2


 - кривизна
- кривизна

 береться «мінус»
береться «мінус» .
. Рис. 3.3
Рис. 3.3
 і цей ефект не враховується.
і цей ефект не враховується.
 ,
,  ,
, (наприклад, для металу Е =2 105 Мпа),
(наприклад, для металу Е =2 105 Мпа), Рис. 3.4
Рис. 3.4
 2)
2) 
 .
.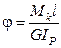 .
. ,
, .
. ,
, ,
,
 , де P – навантаження, f – деформація стержня, k – коефіцієнт пропорційності. Розшифрування коефіцієнта k стало можливим через 130 років, коли англієць Томас Юнг у 1807 р. ввів поняття про модуль пружності Е, названий його ім’ям. Тепер можна було записати
, де P – навантаження, f – деформація стержня, k – коефіцієнт пропорційності. Розшифрування коефіцієнта k стало можливим через 130 років, коли англієць Томас Юнг у 1807 р. ввів поняття про модуль пружності Е, названий його ім’ям. Тепер можна було записати  , де l – довжина стержня, F – площа поперечного перерізу, Е – модуль Юнга, Р – навантаження (сила). Юнг же і визначив значення Е для сталей, як 2·105 МПа. У 1784 р. французький фізик Кулон сформулював закон Гука при скрученні стержня
, де l – довжина стержня, F – площа поперечного перерізу, Е – модуль Юнга, Р – навантаження (сила). Юнг же і визначив значення Е для сталей, як 2·105 МПа. У 1784 р. французький фізик Кулон сформулював закон Гука при скрученні стержня  . У 1826 р. французький інженер (потім академік) А.Нав’є видав перший підручник з опору матеріалів, в якому ввів поняття про напруження (як силу, що діє на одиницю площі перерізу) і записав
. У 1826 р. французький інженер (потім академік) А.Нав’є видав перший підручник з опору матеріалів, в якому ввів поняття про напруження (як силу, що діє на одиницю площі перерізу) і записав  (через 150 років після оприлюднення закону Гука), а також отримав відому формулу для нормальних напружень при згині стержня
(через 150 років після оприлюднення закону Гука), а також отримав відому формулу для нормальних напружень при згині стержня  . Згодом Нав’є ввів поняття про допустимі напруження, умову міцності, О.Коші – поняття про головні напруження і головні деформації, Пуассон ввів свій «коефіцієнт Пуассона». Таким чином, загальними зусиллями в основному цих трьох видатних французів закон Гука постав у закінченому вигляді «узагальненого закону Гука». Тобто, до фундаментальних понять про напруження і деформації людство йшло майже два століття, хоч до них впритул наблизився Юнг і, навіть, близько був ще Галілей (1564-1642).
. Згодом Нав’є ввів поняття про допустимі напруження, умову міцності, О.Коші – поняття про головні напруження і головні деформації, Пуассон ввів свій «коефіцієнт Пуассона». Таким чином, загальними зусиллями в основному цих трьох видатних французів закон Гука постав у закінченому вигляді «узагальненого закону Гука». Тобто, до фундаментальних понять про напруження і деформації людство йшло майже два століття, хоч до них впритул наблизився Юнг і, навіть, близько був ще Галілей (1564-1642).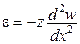 .
. - рівняння сумісності деформацій,
- рівняння сумісності деформацій,  .
.
 - рівняння рівноваги.
- рівняння рівноваги.
 Рис. 3.5
Рис. 3.5

 Будемо умовно вважати, що індексами «1» позначені точки, у яких задані силові характеристики
Будемо умовно вважати, що індексами «1» позначені точки, у яких задані силові характеристики
 ,
,
 .
.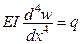 .
. ,
,  .
. ,
,  ,
,  .
.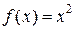 це відома властивість дотичної до параболи. Для форми
це відома властивість дотичної до параболи. Для форми  маємо
маємо  і
і  .
. .
. , щ.м.б.д.
, щ.м.б.д.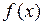 опукла функція векторного змінного
опукла функція векторного змінного  (тобто квадратична форма
(тобто квадратична форма  позитивно визначена). Тоді перетворення Лежандра називається функція
позитивно визначена). Тоді перетворення Лежандра називається функція  векторного змінного
векторного змінного  , що визначена аналогічними попередніми рівностями
, що визначена аналогічними попередніми рівностями ,
, .
. і
і  , які пов’язані між собою перетворенням Лежандра є двоїстими за Юнгом.
, які пов’язані між собою перетворенням Лежандра є двоїстими за Юнгом. .
. Рис. 7.5
Рис. 7.5
 Рис. 7.6
Рис. 7.6


 ,
де
,
де  – двоїсті за Юнгом функції.
– двоїсті за Юнгом функції.
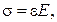


 Приклад 3
Приклад 3



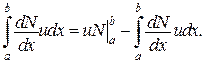

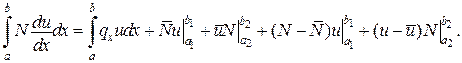
 (див. рис.)
(див. рис.)









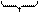




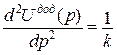
 , гесіан якої відмінний від нуля:
, гесіан якої відмінний від нуля: (1)
(1) . (2)
. (2) :
: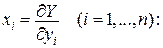 (3)
(3) . (4)
. (4) , тобто
, тобто  то Y теж включає ці параметри, тобто
то Y теж включає ці параметри, тобто  і
і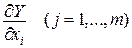 . (5)
. (5) через
через  :
: .
. виражена формулою (4), в якій змінні
виражена формулою (4), в якій змінні  замінені виразами (15). Тоді
замінені виразами (15). Тоді .
. ще і параметри
ще і параметри  .
.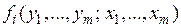 , тому
, тому
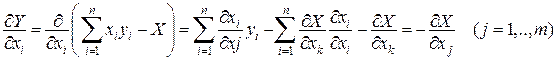 .
.
 Рис. 7.8
Рис. 7.8


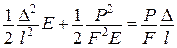


 При деформації
При деформації 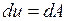 і, відповідно,
і, відповідно,
 ,
,
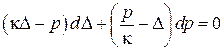
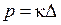 і сумісності деформацій
і сумісності деформацій 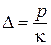 .
. ), то має місце залежність:
), то має місце залежність:
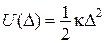







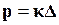






 Рис. 8.9
Рис. 8.9







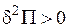














 ,
, де
де  - відомі функції, які задовольняють граничним умовам:
- відомі функції, які задовольняють граничним умовам: