
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклади реалізації принципів Лагранжа і Кастільяно.
Розглянемо розв'язання задачі згину балки (рис. 8.6), яка має кінематичне навантаження у вигляді просідання правої опори на величину
Таким чином екстремальні значення функціоналів Лагранжа і Кастільяно співпадають. Функціонал Лагранжа інколи називається повною потенціальною енергією системи і дорівнює сумі потенціальної енергій пружної деформації і роботи зовнішніх сил.
Перетворення Лежандра
Принцип Лагранжа-Дирихле Для консервативної системи стійка, нестійка, байдужа рівновага мають місце відповідно:
Приклади. Теорема Кастільяно
Теорема Клапейрона
Відповідні екстремальні значення функціоналів Лагранжа і Кастільяно співпадають. Варіаційні рівняння функціоналів Лагранжа і Кастільяно утворюють так звану пару двоїстих задач варіаційного числення, коли попередні умови однієї задачі є природними умовами іншої і навпаки. Під природними умовами розуміються умови, яким задовольняють відповідні варіаційні рівняння.
За допомогою методу множників Лагранжа можна “поміняти місцями” додаткові і природні умови, тобто із функціонала Лагранжа отримати функціонал Кастільяно і навпаки. Таке перетворення у варіаційному численні має назву перетворення Фрідріхса. Зазначимо, що екстремальні значення функціоналів Лагранжа і Кастільяно, а також усіх функціоналів, які отримані за допомогою множників Лагранжа співпадають. Лекція 9
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 186; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.182.105 (0.006 с.) |
 , користуючись принципами
, користуючись принципами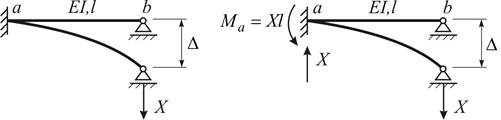 Рис. 8.6
Рис. 8.6
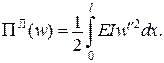
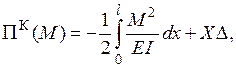
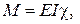
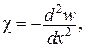
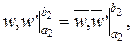
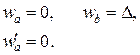
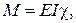

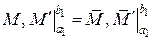 ,
або
,
або
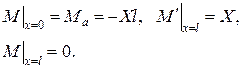
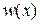 у вигляді ряду:
у вигляді ряду:
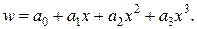 Тоді
Тоді
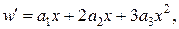
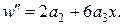
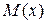 у вигляді ряду:
у вигляді ряду:
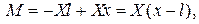 який задовольняє статичним граничним умовам і умові рівноваги
який задовольняє статичним граничним умовам і умові рівноваги
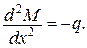
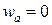 ,
, 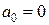 ,
,
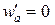 ,
, 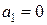 ,
,
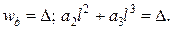 ,
Звідси
,
Звідси
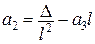 і
і
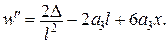
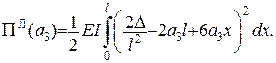
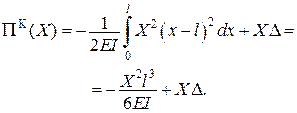
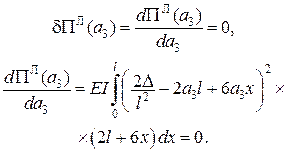
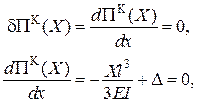
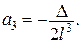 Тоді
Тоді
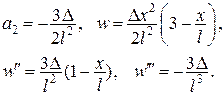
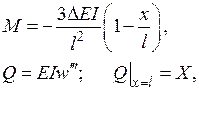
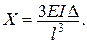

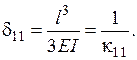 Рівняння методу сил має вигляд
Рівняння методу сил має вигляд
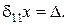
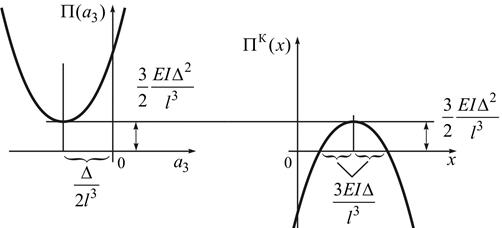
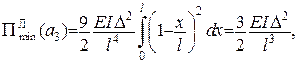 а залежність
а залежність 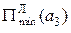 від
від 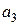 показана на рис. 8.7, а.
показана на рис. 8.7, а.
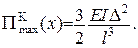 Оскільки
Оскільки
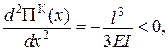 Це є максимум, а залежність
Це є максимум, а залежність 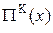 від x показана на рис. 8.7, б.
від x показана на рис. 8.7, б.
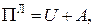
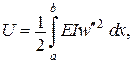
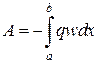 .
.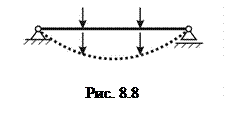 При цьому потенціальна енергія пружної деформації ототожнюється з роботою внутрішніх сил і є позитивною. Робота зовнішніх сил обчислюється як добуток сили на відповідне переміщення (без коефіцієнту ½) і вважається негативною. Функціонал Лагранжа або повна потенціальна енергія інколи трактується як енергія, яка витрачається при переході системи від деформованого стану до первісного.
При цьому потенціальна енергія пружної деформації ототожнюється з роботою внутрішніх сил і є позитивною. Робота зовнішніх сил обчислюється як добуток сили на відповідне переміщення (без коефіцієнту ½) і вважається негативною. Функціонал Лагранжа або повна потенціальна енергія інколи трактується як енергія, яка витрачається при переході системи від деформованого стану до первісного. Рис. 8.9
Рис. 8.9







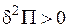





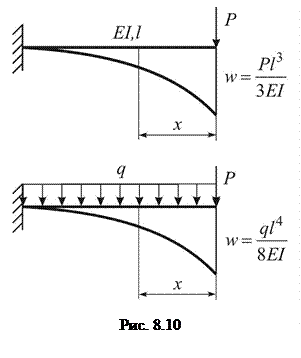
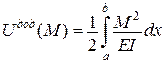 ,
,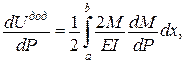
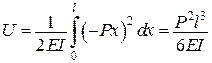 .
.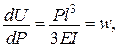
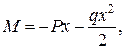
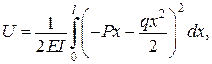
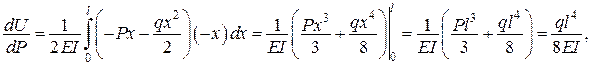
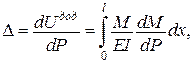
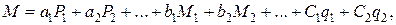
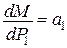 , тобто
, тобто  при
при 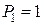
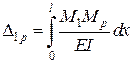 .
.










