
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямі методи варіаційного числення. Поняття про прямі методи. Принципові схеми методу Рітца, узагальненого методу Бубнова-Гальоркіна, методу Бубнова-Гальоркіна, методу Треффца
Поняття про прямі методи. 1) 2) де 3) 4) Суть прямих методів варіаційного числення полягає у тому, що за допомогою розкладу 2) задача про екстремум функціонала 1) зводиться до задачі про екстремум функції багатьох змінних 3), яка розв’язується традиційним методом 4) і призводить до системи алгебраїчних рівнянь відносно невідомих Основні підходи прямих методів.
I. w обрані таким чином, що не усі граничні умови задовольняються:
Тоді застосовується звичайна процедура методу Рітца: 1.1 1.2
Таким чином, отримали вираз (♦), який являє собою систему алгебраїчних рівнянь, після розв’язку яких знаходимо невідомі a 1 ,a 2 ,... ai … an, які містяться у виразах для відповідних похідних Наприклад, якщо
а
Такий підхід має назву узагальненого методу І.Г.Бубнова-Б.Г.Гальоркіна. II.
з якої знаходяться невідомі коефіцієнти a 1 ,a 2 ,... ai … an .. Такий підхід має назву методу І.Г.Бубнова - Б.Г.Гальоркіна.
III. Метод Треффца. Функції
Тоді вираз
з якої знаходяться невідомі a 1 ,a 2 ,... ai … an . . Такий підхід має назву метод Треффца, який запропонував його 1 926 р., а у 1933 р. він був застосований Л.С.Лейбензоном. Таким чином, найбільш загальними є методи Рітца і узагальнений метод Бубнова-Гальоркіна, які не потребують задовільняння усім граничним умовам, що значно розширює можливості при виборі системи базисних функцій
Лекція 10 Канонічні рівняння методу Рітца для функціонала Лагранжа. Приклад.
Повна потенціальна енергія системи дорівнює
де
Застосуємо загальну процедуру методу Рітца
Тоді

Отримаємо систему лінійних алгебраїчних рівнянь
де невідомі –
Приклад Задаємо w у вигляді ряду:
Запишемо їх у вигляді таблиці:
Обчислимо відповідні коефіцієнти матриці алгебраїчних рівнянь (матриці жорсткості):
Вектор навантажень Система алгебраїчних рівнянь має вигляд:
Якщо у вихідному розкладі взяти лише один член
Точний розв’язок
Відповідно, два члени
Такий же результат отримаємо і при наявності розкладу
Лекція 11
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 200; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.179.119 (0.02 с.) |

 ,
, ,
, – відомі функції, які задовольняють певним умовам, наприклад, граничним,
– відомі функції, які задовольняють певним умовам, наприклад, граничним,  – невідомі
– невідомі  .
. ,
, ,
,  ,
,  .
. ,
,  .
. ,
,










 , або у розгорнутому вигляді
, або у розгорнутому вигляді

 ,
, (♦)
(♦)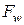 ,
,  .
.

 ,
,  ,
, 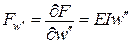 ,
, ,
,  .
. дає систему алгебраїчних рівнянь:
дає систему алгебраїчних рівнянь: ,
, ,
,
 .
. дає систему алгебраїчних рівнянь
дає систему алгебраїчних рівнянь ,
, . Метод Бубнова-Гальоркіна і метод Треффца з цієї точку зору є частиними випадками, відповідно, при
. Метод Бубнова-Гальоркіна і метод Треффца з цієї точку зору є частиними випадками, відповідно, при  Разом з тим, слід мати на увазі, що метод Бубнова-Гальоркіна безпосередньо не пов’язаний із варіаційним численням і може розглядатись як метод розв’язування диференціальних рівнянь і відноситься до так званих проекційних методів або методів ортогоналізації
Разом з тим, слід мати на увазі, що метод Бубнова-Гальоркіна безпосередньо не пов’язаний із варіаційним численням і може розглядатись як метод розв’язування диференціальних рівнянь і відноситься до так званих проекційних методів або методів ортогоналізації
 ,
, – потенціальна енергія пружної деформації,
– потенціальна енергія пружної деформації, ,
, робота зовнішніх сил (рис. 10.1).
робота зовнішніх сил (рис. 10.1).








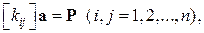
 , коефіцієнти матриці
, коефіцієнти матриці  , вектор навантажень –
, вектор навантажень – 
 .
. ,
, де
де  - відомі функції, які задовольняють граничним умовам:
- відомі функції, які задовольняють граничним умовам:
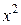










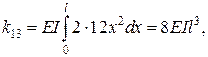
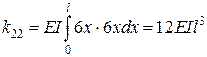 ,
, ,
, 
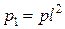 ,
, 



 ,
,

 .
. .
.

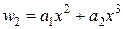 ,
, ,
, 
 (точний розв’язок).
(точний розв’язок). ,
,  .
.


