
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулы, выражающие центральную предельную теорему и встречающиеся при ее практическом применении.⇐ ПредыдущаяСтр 11 из 11
Согласно центральной предельной теореме, закон распределения суммы достаточно большого числа независимых случайных величин (при соблюдении некоторых нежестких ограничений) сколь угодно близок к нормальному. Практически центральной предельной теоремой можно пользоваться и тогда, когда речь идет о сумме сравнительно небольшого числа случайных величин. При суммировании независимых случайных величин, сравнимых по своему рассеиванию, с увеличением числа слагаемых закон распределения суммы очень скоро становится приблизительно нормальным. На практике вообще широко применяется приближенная замена одних законов распределения другими; при той сравнительно малой точности, которая требуется от вероятностных расчетов, такая замена тоже может быть сделана крайне приближенно. Опыт показывает, что когда число слагаемых порядка десяти (а часто и меньше), закон распределения суммы обычно может быть заменен нормальным. В практических задачах часто применяют центральную предельную теорему для вычисления вероятности того, что сумма нескольких случайных величин окажется в заданных пределах. Пусть ξ1, ξ2,..., ξп - независимые случайные величины с математическими ожиданиями т 1, т 2,..., тп и дисперсиями D1,D2,...,Dп. Предположим что условия центральной предельной теоремы выполнены (величины ξ1, ξ2,..., ξп сравнимы по порядку своего влияния на рассеивание суммы) и число слагаемых п достаточно для того, чтобы закон распределения величины η= можно было считать приближенно нормальным. Тогда вероятность того, что случайная величина η попадает в пределы участка (α, β), выражается формулой P(α<η<β)=Ф где тη, ση - математическое ожидание и среднее квадратическое отклонение величины η, Ф - нормальная функция распределения. Согласно теоремам сложения математических ожиданий и дисперсий
Таким образом, для того чтобы приближенно найти вероятность попадания суммы большого числа случайных величин на заданный участок, не требуется знать законы распределения этих величин; достаточно знать лишь их характеристики. Разумеется, это относится только к случаю, когда выполнено основное условие центральной предельной теоремы - равномерно малое влияние слагаемых на рассеивание суммы.
На практике часто применяются формулы, в которых вместо суммы случайных величин ξi фигурирует их нормированная сумма θ = Очевидно, M [ θ ]=0; D [ θ ]= σθ= 1. И в этом случае закон распределения величины θ близок к нормальному с параметрами mθ=0, σθ=1. Отсюда P(α<θ<β)=Ф(β)-Ф(α). Заметим, что центральная предельная теорема может применяться не только к непрерывным, но и к дискретным случайным величинам при условии, что мы будем оперировать не плотностями, а функциями распределения. Действительно, если величины ξ1, ξ2,..., ξп дискретны, то их сумма ξ - также дискретная случайная величина и поэтому, строго говоря, не может подчиняться нормальному закону. Однако все соотношения остаются в силе, так как в них фигурируют не плотности, а функции распределения. Можно доказать, что если дискретные случайные величины удовлетворяют условиям центральной предельной теоремы, то функция распределения их нормированной суммы θ при увеличении п неограниченно приближается к нормальной функции распределения с параметрами mθ= 0, σθ= 1. Частным случаем центральной предельной теоремы для дискретных случайных величин является теорема Лапласа. Теорема. Если производится п независимых опытов, в каждом из которых событие А появляется с вероятностью р, то справедливо соотношение P(α< где η - число появлений события А в п опытах, q=1-р. Доказательство. Пусть производится п независимых опытов, в каждом из которых с вероятностью р может появиться событие А. Представим случайную величину η - общее число появлений события в п опытах - в виде суммы η= где ξi - число появлений события А в i -м опыте. Согласно центральной предельной теореме, закон распределения суммы одинаково распределенных слагаемых при увеличении их числа приближается к нормальному закону. Следовательно, при достаточно большом п справедлива формула P (α < θ < β)=Ф(β)-Ф(α), где θ = Математическое ожидание и дисперсия числа появлений события в п независимых опытах равны: тη=пр, Dη=npq (q=1-р).
С учетом этого получим θ = и окончательно можно записать: P (α < Теорема доказана.
§33. Цепи Маркова
Определение. Цепью Маркова называют последовательность испытаний, в каждом из которых появляется только одно из k несовместных событий А1, A2, ..., Ak полной группы, причем условная вероятность pij (s) того, что в s -м испытании наступит событие Aj (j=1,2,...,k), при условии, что в (s-1)- м испытании наступило событие Ai (i=1,2,...,k), не зависит от результатов предшествующих испытаний. Например, если последовательность испытаний образует цепь Маркова и полная группа состоит из четырех несовместных событий А1, A2, A3, A4, причем известно, что в шестом испытании появилось событие A2, то условная вероятность того, что в седьмом испытании наступит событие A4, не зависит от того, какие события появились в первом, втором,..., пятом испытаниях. Заметим, что независимые испытания являются частным случаем цепи Маркова. Действительно, если испытания независимы, то появление некоторого определенного события в любом испытании не зависит от результатов ранее произведенных испытаний. Отсюда следует, что понятие цепи Маркова является обобщением понятия независимых испытаний. Далее используется терминология, которая принята при изложении цепей Маркова. Пусть некоторая система в каждый момент времени находится в одном из k состояний: первом, втором,..., k -м. В отдельные моменты времени в результате испытания состояние системы изменяется, т. е. система переходит из одного состояния, например i, в другое, например j. В частности, после испытания система может остаться в том же состоянии («перейти» из состояния i в состояние j = i). Таким образом, события называют состояниями системы, а испытания - изменениями ее состояний. Дадим теперь определение цепи Маркова, используя новую терминологию. Определение. Цепью Маркова называют последовательность испытаний, в каждом из которых система принимает только одно из k состояний полной группы, причем условная вероятность pij (s)того, что в s -м испытании система будет находиться в состоянии j, при условии, что после (s-1)- го испытания она находилась в состоянии i, не зависит от результатов остальных, ранее произведенных испытаний. Определение. Цепью Маркова с дискретным временем называют цепь, изменение состояний которой происходит в определенные фиксированные моменты времени. Определение. Цепью Маркова с непрерывным временем называют цепь, изменение состояний которой происходит в любые случайные возможные моменты времени. Определение. Однородной называют цепь Маркова, если условная вероятность pij (s)(перехода из состояния i в состояние j) не зависит от номера испытания. Поэтому вместо pij (s) пишут просто pij. Пример. Случайное блуждание. Пусть на прямой OX в точке с целочисленной координатой x = n находится материальная частица. В определенные моменты времени t1, t2, t3,... частица испытывает толчки. Под действием толчка частица с вероятностью р смещается на единицу вправо и с вероятностью 1-р - на единицу влево. Ясно, что положение (координата) частицы после толчка зависит от того, где находилась частица после непосредственно предшествующего толчка, и не зависит от того, как она двигалась под действием остальных предшествующих толчков.
Таким образом, случайное блуждание - пример однородной цепи Маркова с дискретным временем. Далее ограничимся элементами теории конечных однородных цепей Маркова. Определение. Переходной вероятностью pij называют условную вероятность того, что из состояния i (в котором система оказалась в результате некоторого испытания, безразлично какого номера) в итоге следующего испытания система перейдет в состояние j. Таким образом, в обозначении pij первый индекс указывает номер предшествующего, а второй - номер последующего состояния. Например, р11 - вероятность «перехода» из первого состояния в первое; р23 - вероятность перехода из второго состояния в третье. Пусть число состояний конечно и равно k. Определение Матрицей перехода системы называют матрицу, которая содержит все переходные вероятности этой системы: P1 = Так как в каждой строке матрицы помещены вероятности событий (перехода из одного и того же состояния i в любое возможное состояние j), которые образуют полную группу, то сумма вероятностей этих событий равна единице. Другими словами, сумма переходных вероятностей каждой строки матрицы перехода равна единице:
Приведем пример матрицы перехода системы, которая может находиться в трех состояниях: P1= Здесь р11=0,5 - вероятность перехода из состояния i = 1 в это же состояние j = 1; p21 = 0,4 - вероятность перехода из состояния i = 2 в состояние j = 1. Аналогичный смысл имеют остальные элементы матрицы. Равенство Маркова.
Обозначим через Рij (п) вероятность того, что в результате п шагов (испытаний) система перейдет из состояния i в состояние j. Например, Р25 (10) - вероятность перехода за 10 шагов из второго состояния в пятое. Подчеркнем, что при п = 1 получим переходные вероятности Рij (1)= pij. Поставим перед собой задачу: зная переходные вероятности pij,найти вероятности Рij (п) перехода системы из состояния i в состояние j за п шагов. С этой целью введем в рассмотрение промежуточное (между i и j) состояние r. Другими словами, будем считать, что из первоначального состояния i за т шагов система перейдет в промежуточное состояние r с вероятностью Pir (m), после чего за оставшиеся п - т шагов из промежуточного состояния r она перейдет в конечное состояние j с вероятностью Prj (n-т). По формуле полной вероятности, Рij (п)= Эту формулу называют равенством Маркова (также данное соотношение называют формулой Чепмена-Колмогорова).
Пояснение. Введем обозначения: А - интересующее нас событие (за п шагов система перейдет из начального состояния i в конечное состояние j), следовательно, Р (А)= Рij (п); Вr (r=1,2,...,k)- гипотезы (за т шагов система перейдет из первоначального состояния i в промежуточное состояние r), следовательно, Р (Br)= Pir (m); P По формуле полной вероятности, Р (А)= или в принятых нами обозначениях Pij (n)=
Покажем, что, зная все переходные вероятности pij = Рij (1), т. е. зная матрицу P1 перехода из состояния в состояние за один шаг, можно найти вероятности Рij(2) перехода из состояния в состояние за два шага, следовательно, и саму матрицу перехода P2; по известной матрице P2 можно найти матрицу P3 перехода из состояния в состояние за 3 шага, и т. д. Действительно, положив n=2, т =1в равенстве Маркова Pij (n)= получим Pij(2) = или Pij(2)= Таким образом, можно найти все вероятности Р ij(2), следовательно, и саму матрицу P2. Напишем полученное соотношение в матричной форме: P2=P1P1=P Положив п=3, т=2 аналогично получим P3=P1P2=P1P В общем случае Pn=P Пример. Задана матрица перехода P1= Решение. Воспользуемся формулой P2=P P2= Перемножив матрицы, окончательно получим P2=
|
||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 207; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.130.31 (0.046 с.) |

 -Ф
-Ф  ,
,
 =
=  .
. <β)=Ф(β)-Ф(α).
<β)=Ф(β)-Ф(α). .
. .
. =1 (i=1,2,…,k).
=1 (i=1,2,…,k). .
.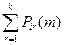 Prj (n-т).
Prj (n-т). (A)- условная вероятность наступления А при условии, что имела место гипотеза Вr (за п - т шагов система перейдет из промежуточного состояния r в конечное состояние j), следовательно, P
(A)- условная вероятность наступления А при условии, что имела место гипотеза Вr (за п - т шагов система перейдет из промежуточного состояния r в конечное состояние j), следовательно, P  P
P  Prj(2-1),
Prj(2-1),
 .
. .
. .
. . Найти матрицу перехода P2=
. Найти матрицу перехода P2=  .
. .
.


