
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства характеристических функций.
Свойство 1. Характеристическая функция всегда существует: |φξ(t)|=|Meitξ|≤M | eitξ|=M1=1 Обычные математические ожидания существуют не у всех распределений. Свойство 2. По характеристической функции однозначно восстанавливается распределение (функция распределения, а также плотность или таблица распределения). То есть если две случайные величины имеют одинаковые характеристические функции, то и распределения этих случайных величин совпадают. Формулы, с помощью которых это делается, в анализе называют формулами «обратного преобразования Фурье». Например, если модуль характеристической функции интегрируем на всей прямой, то у случайной величины есть плотность распределения, и она находится по формуле fξ (x)= Ни одна из формул обратного преобразования Фурье нам не понадобится. Свойство 3. Характеристическая функция случайной величины а+bξ связана с характеристической функцией случайной величины равенством φа + bξ (t)= Meit (а + bξ )= eitа φξ (tb). Пример. Вычислим характеристическую функцию случайной величины ξ, имеющей нормальное распределение с параметрами а и σ2. У стандартизованной случайной величины ζ = φξ (t)= φа + σζ (t)= eitа φζ (tb)= eitа Свойство 4. Характеристическая функция суммы независимых случайных величин равна произведению характеристических функций слагаемых: если случайные величины ξ и η независимы, то, по свойству математических ожиданий φξ+η (t)= Meit ( ξ+η )= MeitξMeitη = φξ (t) φη (t). Этим свойством воспользуемся для доказательства леммы, утверждающей устойчивость нормального распределения относительно суммирования. Лемма. Пусть случайные величины ξ φξ+η (t)= φξ (t) φη (t)=exp То есть характеристическая функция суммы есть характеристическая функция нормального распределения с параметрами а 1+ а 2, Пример. Докажем свойства устойчивости по суммированию биномиального распределения и распределения Пуассона, используя вычисленные в предыдущих примерах характеристические функции.
Для независимых случайных величин с распределениями Пуассона Пλ и Пμ характеристическая функция суммы φξ+η(t)=φξ(t)φη(t)=ехр{λ(еit-1)}ехр{μ(еit-l)}=ехр{(λ+μ)(еit-l)} равна характеристической функции распределения Пуассона с параметром λ+μ. Для независимых случайных величин с биномиальными распределениями Вп,р и Вт,р характеристическая функция суммы φξ+η(t)=φξ(t)φη(t)=(1-р+рeit)n(1-р+рeit)т=(1-р+рeit)n+т равна характеристической функции биномиального распределения с параметрами п + m, p. Свойство 5. Пусть существует момент порядка k=1,2,... случайной величины ξ, то есть M | ξ | k <∞. Тогда ее характеристическая функция φξ (t)непрерывно дифференцируема k раз, и ее k -япроизводная в нулесвязана с моментом порядка k равенством:
Существование и непрерывность k- йпроизводной, равно как и законность переноса производной под знак математического ожидания мы доказывать не будем. Свойство 6. Пусть существует момент порядка k=1,2,... случайной величины ξ, то есть M | ξ | k <∞. Тогда ее характеристическая функция φξ (t)в окрестности точки t =0 разлагается в ряд Тейлора φξ(t)=φξ(0)+ =1+itMξ- Ряды Тейлора, как правило, возникают при предельном переходе. Следующее основное свойство характеристических функций потребуется нам для доказательства предельных теорем. Теорема (о непрерывном соответствии). Случайные величины ξп слабо сходятся к случайной величине ξ тогда и только тогда, когда для любого t характеристические функции Слабая сходимость случайных величин имеет место, когда последовательность функций распределений случайных величин ξп сходится к функции распределения случайной величины x в точках непрерывности последней. Сформулированная теорема устанавливает непрерывное соответствие между классами функций распределения со слабой сходимостью и характеристических функций со сходимостью в каждой точке. «Непрерывность» этого соответствия - в том, что пределу в одном классе относительно заданной в этом классе сходимости соответствует предел в другом классе относительно сходимости, заданной в этом классе.
§32. Центральная предельная теорема
Известно, что нормально распределенные случайные величины широко распространены на практике. Чем это объясняется? Ответ на этот вопрос был дан выдающимся русским математиком А.М.Ляпуновым (центральная предельная теорема): если случайная величина ξ представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то ξ имеет распределение, близкое к нормальному. Пример. Пусть производится измерение некоторой физической величины. Любое измерение дает лишь приближенное значение измеряемой величины, так как на результат измерения влияют очень многие независимые случайные факторы (температура, колебания прибора, влажность и др.). Каждый из этих факторов порождает ничтожную «частную ошибку». Однако, поскольку число этих факторов очень велико, их совокупное действие порождает уже заметную «суммарную ошибку». Рассматривая суммарную ошибку как сумму очень большого числа взаимно независимых частных ошибок, можно заключить, что суммарная ошибка имеет распределение, близкое к нормальному. Опыт подтверждает справедливость такого заключения. Приведем формулировку центральной предельной теоремы, которая устанавливает условия, при которых сумма большого числа независимых слагаемых имеет распределение, близкое к нормальному. Пусть ξ1, ξ2,..., ξп,... - последовательность независимых случайных величин, каждая из которых имеет конечные математическое ожидание и дисперсию: M (ξk)= ak, D (ξk)= b Введем обозначения: Sn=ξ1+ξ2+...+ξn, An = Обозначим функцию распределения нормированной суммы через Fn (x)= P Говорят, что к последовательности ξ1, ξ2,... применима центральная предельная теорема, если при любом x функция распределения нормированной суммы при п
В частности, если все случайные величины ξ1, ξ2,... одинаково распределены, то к этой последовательности применима центральная предельная теорема, если дисперсии всех величин ξi (i=1,2,...) конечны и отличны от нуля. А.М.Ляпунов доказал, что если для δ>0 при п Ln = Cn / B стремится к нулю (условие Ляпунова), то к последовательности ξ1, ξ2,... применима центральная предельная теорема. Сущность условия Ляпунова состоит в требовании, чтобы каждое слагаемое суммы (Sn - Ап)/ Вп оказывало на сумму ничтожное влияние.
Центральная предельная теорема для одинаково распределенных слагаемых.
Различные формы центральной предельной теоремы отличаются между собой условиями, накладываемыми на распределения образующих сумму случайных слагаемых. Здесь мы сформулируем и докажем одну из самых простых форм центральной предельной теоремы, относящуюся к случаю одинаково распределенных слагаемых. Теорема. Если ξ1, ξ2,..., ξп,...- независимые случайные величины, имеющие один и тот же закон распределения с математическим ожиданием m и дисперсией σ 2, то при неограниченном увеличении п закон распределения суммы
неограниченно приближается к нормальному. Доказательство. Проведем доказательство для случая непрерывных случайных величин ξ1,..., ξп (для прерывных оно будет аналогичным). Согласно второму свойству характеристических функций характеристическая функция величины ηn представляет собой произведение характеристических функций слагаемых. Случайные величины ξ1,..., ξп имеют один и тот же закон распределения с плотностью f (х) и, следовательно, одну и ту же характеристическую функцию φξ (t)= Следовательно, характеристическая функция случайной величины ηn будет
Исследуем более подробно функцию φξ (t). Представим ее в окрестности точки t =0 по формуле Маклорена с тремя членами: φξ(t)=φξ(0)+ где α(t)→0 при t→0. Найдем величины φξ(0), φξ(0)= Продифференцируем (2) по t:
Полагая в (6) t=0, получим:
Очевидно, не ограничивая общности, можно положить т=0 (для этого достаточно перенести начало отсчета в точку т).Тогда
Продифференцируем (6) еще раз:
отсюда
При m=0 интеграл в выражении (8) есть не что иное, как дисперсия величины ξ с плотностью f (х),следовательно
Подставляя в (4) φξ(0)=1, φξ(t)=1- Обратимся к случайной величине ηn. Мы хотим доказать, что ее закон распределения при увеличении п приближается к нормальному. Для этого перейдем от величины ηn к другой («нормированной») случайной величине θп = Эта величина удобна тем, что ее дисперсия не зависит от п и равна единице при любом п. В этом нетрудно убедиться, рассматривая величину θп как линейную функцию независимых случайных величин ξ1, ξ2,..., ξп, каждая из которых имеет дисперсию σ 2. Если мы докажем, что закон распределения величины θn приближается к нормальному, то, очевидно, это будет справедливо и для величины ηп, связанной с θn линейной зависимостью (11). Вместо того чтобы доказывать, что закон распределения величины θn при увеличении п приближается к нормальному, покажем, что ее характеристическая функция приближается к характеристической функции нормального закона. Найдем характеристическую функцию величины θn. Из соотношения (11), согласно первому свойству характеристических функций, получим
где
Из формул (12) и (3) получим
или, пользуясь формулой (10),
Прологарифмируем выражение (14): ln Введем обозначение
Тогда ln Будем неограниченно увеличивать п. При этом величина x,согласно формуле (15), стремится к нулю. При значительном п ее можно считать весьма малой. Разложим ln{1-х} в ряд и ограничимся одним членом разложения (остальные при n →∞ станут пренебрежимо малыми): ln{1-х}≈-х. Тогда получим
По определению функция α(t) стремится к нулю при t→0; следовательно,
и
откуда
Это есть не что иное, как характеристическая функция нормального закона с параметрами т=0, σ=1. Таким образом, доказано, что при увеличении п характеристическая функция случайной величины θn неограниченно приближается к характеристической функции нормального закона; отсюда заключаем, что и закон распределения величины θn (а значит и величины ηп) неограниченно приближается к нормальному закону. Теорема доказана. Мы доказали центральную предельную теорему для частного, но важного случая одинаково распределенных слагаемых. Однако в достаточно широком классе условий она справедлива и для неодинаково распределенных слагаемых. Например, А.М.Ляпунов доказал центральную предельную теорему для следующих условий:
где bk - третий абсолютный центральный момент величины ξk: bk=ν3[ξk]=M[| Наиболее общим (необходимым и достаточным) условием справедливости центральной предельной теоремы является условие Линдеберга: при любом τ> 0
где mk - математическое ожидание, fk (х) - плотность распределения случайной величины ξk, Bn=
|
||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 897; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.151.106 (0.046 с.) |
 .
. характеристическая функция равна φζ (t)=
характеристическая функция равна φζ (t)=  . Тогда характеристическая функция случайной величины ξ = а + σζ равна
. Тогда характеристическая функция случайной величины ξ = а + σζ равна =exp
=exp  .
. и η
и η  независимы. Характеристическая функция суммы ξ + η равна
независимы. Характеристическая функция суммы ξ + η равна exp
exp  =exp
=exp  .
.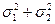 . Тогда ξ + η
. Тогда ξ + η 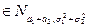 по свойству характеристической функции.
по свойству характеристической функции. =
=  =
= 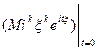 = ikMξk..
= ikMξk.. +o(|tk|)=1+
+o(|tk|)=1+  +o(|tk|)=
+o(|tk|)= Mξ2+…+
Mξ2+…+  Mξk+o(|tk|).
Mξk+o(|tk|). сходятся к характеристической функции φξ (t).
сходятся к характеристической функции φξ (t). .
. , B2 =
, B2 =  .
. .
. стремится к нормальной функции распределения:
стремится к нормальной функции распределения: P
P  =
= 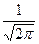
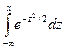 .
. , где Cn =
, где Cn =  | ξk – ak | 2+δ,
| ξk – ak | 2+δ, (1)
(1) (2)
(2) (t)=[ φξ (t)] n. (3)
(t)=[ φξ (t)] n. (3) (0)t+
(0)t+  t2, (4)
t2, (4) (0). Полагая в формуле (2) t=0, имеем:
(0). Полагая в формуле (2) t=0, имеем: =1. (5)
=1. (5)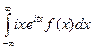 =i
=i  (6)
(6)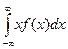 =iM[ξ]=im. (7)
=iM[ξ]=im. (7) ,
,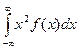 . (8)
. (8) t2. (10)
t2. (10) (11)
(11) , (12)
, (12) характеристическая функция случайной величины ηп.
характеристическая функция случайной величины ηп.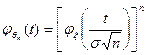 (13)
(13) . (14)
. (14) .
. = x. (15)
= x. (15)
 (t)=
(t)= 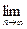 n (- x)=
n (- x)=  =-
=-  .
. =0
=0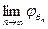 (t)=
(t)=  . (16)
. (16) =0,
=0, |3] (k=1,…,n), Dk - дисперсия величины ξk.
|3] (k=1,…,n), Dk - дисперсия величины ξk. =0,
=0, .
.


