
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функция двух случайных аргументов.
Определение. Если каждой паре возможных значений случайных величин ξ и η соответствует одно возможное значение случайной величины θ, то θ называют функцией двух случайных аргументов ξ и η: θ = φ (ξ, η). Необходимо найти распределение функции θ = ξ+η по известным распределениям слагаемых. Такая задача часто встречается на практике. Например, если ξ - погрешность показаний измерительного прибора (распределена нормально), η - погрешность округления показаний до ближайшего деления шкалы (распределена равномерно), то возникает задача - найти закон распределения суммы погрешностей θ = ξ+η. 1. Пусть ξ и η - дискретные независимые случайные величины. Для того, чтобы составить закон распределения функции θ = ξ+η,надо найти все возможные значения θ и их вероятности. Пример. Дискретные независимые случайные величины заданы распределениями:
Составить распределение случайной величины θ = ξ+η. Решение. Возможные значения θ есть суммы каждого возможного значения ξ со всеми возможными значениями η: z1=1+3=4; z2=1+4=5; z3=2+3=5; z4=2+4=6. Найдем вероятности этих возможных значений. Для того чтобы θ=4, достаточно, чтобы величина ξ приняла значение х1=1 и величина η - значение y1=3. Вероятности этих возможных значений, как следует из данных законов распределения, соответственно равны 0,4 и 0,2. Аргументы ξ и η независимы, поэтому события ξ =1 и η =3 независимы и, следовательно, вероятность их совместного наступления (то есть вероятность события θ = 1+3=4) по теореме умножения равна 0,4·0,2=0,08. Аналогично найдем: P(θ=1+4=5)=0,4·0,8=0,32; P(θ=2+3=5)=0,6·0,2=0,12; P(θ=2+4=6)=0,6·0,8=0,48. Напишем искомое распределение, сложив предварительно вероятности несовместных событий θ=z2, θ=z3, (0,32+0,12=0,44):
Контроль: 0,08+0,44+0,48=1. 2. Пусть ξ и η - непрерывные случайные величины. Доказано: если ξ и η независимы, то плотность распределения g (z) суммы θ=ξ+η (при условии, что плотность хотя бы одного из аргументов задана на интервале (-∞,∞) одной формулой) может быть найдена с помощью равенства g (z)= либо с помощью равносильного равенства
g (z)= где f1, f2 - плотности распределения аргументов. Если возможные значения аргументов неотрицательны, то g (z) находят по формуле g (z)= либо по равносильной формуле g (z)= Определение. Плотность распределения суммы независимых случайных величин называют композицией. Определение. Закон распределения вероятностей называют устойчивым,если композиция таких законов есть тот же закон (отличающийся, вообще говоря, параметрами). Нормальный закон обладает свойством устойчивости: композиция нормальных законов также имеет нормальное распределение (математическое ожидание и дисперсия этой композиции равны соответственно суммам математических ожиданий и дисперсий слагаемых). Например, если ξ и η - независимые случайные величины, распределенные нормально с математическими ожиданиями и дисперсиями, соответственно равными а1=3, а2=4, D1=l, D2=0,5, то композиция этих величин (то есть плотность вероятности суммы θ = ξ+η) также распределена нормально, причем математическое ожидание и дисперсия композиции соответственно равны а=3+4=7; D=l+0,5=1,5. Пример. Независимые случайные величины ξ и η заданы плотностями распределений: f (x)= f (y)= Найти композицию этих законов, то есть плотность распределения случайной величины θ = ξ+η. Решение. Возможные значения аргументов неотрицательны, поэтому g (z)= Здесь z ≥ 0, так как θ = ξ+η и, по условию, возможные значения ξ и η неотрицательны и имеет место равенство
§28. Условное математическое ожидание
Важной характеристикой условного распределения вероятностей является условное математическое ожидание. Определение. Условным математическим ожиданием дискретной случайной величины η при ξ = х (х - определенное возможное значение ξ) называют произведение возможных значений η на их условные вероятности: M (η | ξ = х)= Для непрерывных величин M (η | ξ = х)= где ψ(y|x) - условная плотность случайной величины η при ξ = х. Условное математическое ожидание M (η | х) есть функция от х:
M (η | х)= f (x), которую называют функцией регрессии η на ξ. Аналогично определяются условное математическое ожидание случайной величины ξ и функция регрессии ξ на η: Пример. Дискретная двумерная случайная величина задана таблицей значений.
Найти условное математическое ожидание составляющей η при ξ = х1=1. Решение. Найдем р (х1), для чего сложим вероятности, помещенные в первом столбце таблицы: р(х1)=0,15+0,30=0,45. Найдем условное распределение вероятностей величины η при ξ=х1=1: р(у1|х1)=р(х1,y1)/p(х1)=0,15/0,45=1/3; р(у2|х1)=р(х2,y2)/p(х1)=0,30/0,45=2/3. Найдем искомое условное математическое ожидание: M(η|ξ=х1)=
§29. Ковариация. Коэффициент корреляции
Для описания системы двух случайных величин кроме математических ожиданий и дисперсий составляющих используют и другие характеристики; к их числу относятся ковариация (корреляционный момент) и коэффициент корреляции. Определение. Ковариацией случайных величин ξ и η называют математическое ожидание произведения отклонений этих величин: cov(ξ,η)=М{[ξ-M(ξ)][η-M(η)]}. Для вычисления ковариации дискретных величин используют формулу cov(ξ,η)= а для непрерывных величин - формулу cov(ξ,η)= Ковариация служит для характеристики связи между величинами ξ и η. Ковариация равна нулю, если ξ и η независимы; следовательно, если ковариация не равна нулю, то ξ и η - зависимые случайные величины. Отметим, что ковариацию можно определить как математическое ожидание произведения центрированных случайных величин: cov(ξ,η)=М [ 3амечание. Легко убедиться, что ковариацию можно записать в виде cov(ξ,η)=М (ξη)- М (ξ) М (η). Теорема. Ковариация двух независимых случайных величин ξ и η равна нулю. Доказательство. Так как ξ и η - независимые случайные величины, то их отклонения ξ-M (ξ)и η-M (η) также независимы. Пользуясь свойствами математического ожидания (математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий сомножителей) и отклонения (математическое ожидание отклонения равно нулю), получим cov(ξ,η)=М{[ξ-M(ξ)][η-M(η)]}=M[ξ-M(ξ)]M[η-M(η)]=0. Из определения ковариации следует, что она имеет размерность, равную произведению размерностей величин ξ и η. Другими словами, величина ковариации зависит от единиц измерения случайных величин. По этой причине для одних и тех же двух величин величина ковариации имеет различные значения в зависимости от того, в каких единицах были измерены величины. Пусть, например, ξ и η были измерены в сантиметрах и cov(ξ,η) = 2 см2; если измерить ξ и η в миллиметрах, то cov(ξ,η) = 200 мм2. Такая особенность ковариации является недостатком этой числовой характеристики, поскольку сравнение корреляционных моментов различных систем случайных величин становится затруднительным. Для того чтобы устранить этот недостаток, вводят новую числовую характеристику - коэффициент корреляции. Определение. Коэффициентом корреляции r(ξ,η) случайных величин ξ и η называют отношение ковариации к произведению средних квадратических отклонений этих величин:
r(ξ,η) = cov(ξ,η) /( Так как размерность cov(ξ,η) равна произведению размерностей величин ξ и η, Замечание. Во многих вопросах теории вероятностей целесообразно вместо случайной величины ξ рассматривать нормированную случайную величину ξ’, которую определяют как отношение отклонения к среднему квадратическому отклонению: ξ’ =(ξ-M (ξ))/ Нормированная величина имеет математическое ожидание, равное нулю, и дисперсию, равную единице. Действительно, используя свойства математического ожидания и дисперсии, имеем: M(ξ’)=M D(ξ’)=D Легко убедиться, что коэффициент корреляции r(ξ,η) равен ковариации нормированных величин ξ’ и η’: r(ξ,η) = Теорема. Абсолютная величина ковариации двух случайных величин ξ и η не превышает среднего геометрического их дисперсий: | cov(ξ,η) |≤ Доказательство. Введем в рассмотрение случайную величину θ1= D(θ1)=2 Любая дисперсия неотрицательна, поэтому 2 Отсюда cov(ξ,η) ≤ Введя случайную величину θ2= cov(ξ,η) ≥- Объединим неравенства - или | cov(ξ,η) |≤ Итак, | cov(ξ,η) |≤
Теорема. Абсолютная величина коэффициента корреляции не превышает единицы: |r(ξ,η)|≤1. Доказательство: Разделим обе части двойного неравенства - -1≤r(ξ,η)≤1. Итак, |r(ξ,η)|≤1. Определение. Две случайные величины ξ и η называют коррелированными, если их ковариация (или, что то же, коэффициент корреляции) отлична от нуля; ξ и η называют некоррелированными величинами, если их ковариация равна нулю. Две коррелированные величины также и зависимы. Действительно, допустив противное, мы должны заключить, что cov(ξ,η)=0, противоречит условию, так как для коррелированных величин cov(ξ,η)≠0.
Обратное предположение не всегда имеет место, т.е. если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными. Другими словами, корреляционный момент двух зависимых величин может быть не равен нулю, но может и равняться нулю. Убедимся на примере, что две зависимые величины могут быть некоррелированными. Пример. Двумерная случайная величина (ξ, η)задана плотностью распределения: f(x,у)=1/6π внутри эллипса x2/9+y2/4=1; f(x,у)=0 вне этого эллипса. Доказать, что ξ и η - зависимые некоррелированные величины. Решение. Вычислим плотности распределения составляющих ξ и η: f1(x)= Так как f (x, у)≠ f1 (x) f2 (у),то ξ и η - зависимые величины. Для того чтобы доказать некоррелированность ξ и η, достаточно убедиться в том, что cov(ξ,η)=0. Найдем корреляционный момент по формуле cov(ξ,η)= Поскольку функция f1 (x)симметрична относительно оси OY, то М(ξ)=0; аналогично, М(η)=0 в силу симметрии f2 (у) относительно оси OX. Следовательно, cov(ξ,η)= Вынося постоянный множитель f(x, у) за знак интеграла, получим cov(ξ,η) = f (x,y) Внутренний интеграл равен нулю (подынтегральная функция нечетна, пределы интегрирования симметричны относительно начала координат), следовательно, cov(ξ,η)=0,т.е. зависимые случайные величины ξ и η некоррелированы. Итак, из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не вытекает коррелированность. Из независимости двух величин следует их некоррелированность, но из некоррелированности еще нельзя заключить о независимости этих величин. Замечание. Теперь мы можем определить дисперсию суммы двух произвольных случайных величин D(ξ+η)=D(ξ)+D(η)+2cov(ξ,η). Справедливость данного соотношения вытекает непосредственно из доказательства соответствующего свойства дисперсии и определения ковариации. На практике часто встречаются двумерные случайные величины, распределение которых нормально. Определение. Нормальным законом распределения на плоскости называют распределение вероятностей двумерной случайной величины (ξ, η), если f (x, y)= Нормальный закон на плоскости определяется пятью параметрами: a1, a2, σ 1,σ 2 и r. Можно доказать, что эти параметры имеют следующий вероятностный смысл: a1, a2 - математические ожидания, σ 1,σ 2 - средние квадратические отклонения, r - коэффициент корреляции величин ξ и η. Убедимся в том, что если составляющие двумерной нормально распределенной случайной величины некоррелированны, то они и независимы. Действительно, пусть ξ и η некоррелированны. Тогда, полагая в f (x, y)= = Таким образом, если составляющие нормально распределенной случайной величины некоррелированны, то плотность совместного распределения системы равна произведению плотностей распределения составляющих, а отсюда и следует независимость составляющих. Справедливо и обратное утверждение.
Итак, для нормально распределенных составляющих двумерной случайной величины понятия независимости и некоррелированности равносильны.
§30. Закон больших чисел
Как уже известно, нельзя заранее уверенно предвидеть, какое из возможных значений примет случайная величина в итоге испытания; это зависит от многих случайных причин, учесть которые невозможно. Казалось бы, поскольку о каждой случайной величине мы располагаем в этом смысле весьма скромными сведениями, то вряд ли можно установить закономерности поведения и суммы достаточно большого числа случайных величин. На самом деле это не так. Оказывается, что при некоторых сравнительно широких условиях суммарное поведение достаточно большого числа случайных величин почти утрачивает случайный характер и становится закономерным. Для практики очень важно знание условий, при выполнении которых совокупное действие очень многих случайных причин приводит к результату, почти не зависящему от случая, так как позволяет предвидеть ход явлений. Эти условия и указываются в теоремах, носящих общее название закона больших чисел. К ним относятся теоремы Чебышева и Бернулли. Теорема Чебышева является наиболее общим законом больших чисел, теорема Бернулли - простейшим. Для доказательства этих теорем мы воспользуемся неравенством Чебышева. Неравенство Чебышева справедливо для дискретных и непрерывных случайных величин. Для простоты ограничимся доказательством этого неравенства для дискретных величин. Рассмотрим дискретную случайную величину ξ,заданную таблицей распределения:
Поставим перед собой задачу оценить вероятность того, что отклонение случайной величины от ее математического ожидания не превышает по абсолютной величине положительного числа ε. Если ε достаточно мало, то мы оценим, таким образом, вероятность того, что ξ примет значения, достаточно близкие к своему математическому ожиданию. П.Л.Чебышев доказал неравенство, позволяющее дать эту оценку. Теорема. (Неравенство Чебышева) Вероятность того, что отклонение случайной величины ξ от ее математического ожидания по абсолютной величине меньше положительного числа ε, не меньше, чем 1-D(ξ)/ε2: P(|ξ–M(ξ)|<ε)≥1-D(ξ)/ε2. Доказательство. Так как события, состоящие в осуществлении неравенств | ξ - М (ξ)|< ε и | ξ - М (ξ)|≥ ε, противоположны, то сумма их вероятностей равна единице, то есть Р(|ξ-М(ξ)|<ε)+Р(|ξ-М(ξ)|≥ε)=1. Отсюда интересующая нас вероятность Р(|ξ-М(ξ)|<ε)=1-Р(|ξ-М(ξ)|≥ε). Таким образом, задача сводится к вычислению вероятности Р (| ξ-М (ξ)|≥ ε). Напишем выражение дисперсии случайной величины ξ: D(ξ)=[x1-М(ξ)]2p1+[x2-М(ξ)]2p2+…+[xn-М(ξ)]2pn. Очевидно, все слагаемые этой суммы неотрицательны. Отбросим те слагаемые, у которых | xi - М (ξ)|< ε (для оставшихся слагаемых (| xj - М (ξ)|≥ ε), вследствие чего сумма может только уменьшиться. Условимся считать для определенности, что отброшено k первых слагаемых (не нарушая общности, можно считать, что в таблице распределения возможные значения занумерованы именно в таком порядке). Таким образом, D(ξ)≥[xk+1-М(ξ)]2pk+1+[xk+2-М(ξ)]2pk+2+…+[xn-М(ξ)]2pn. Заметим, что обе части неравенства | xj - М (ξ)|≥ ε (j=k+1,k+2,...,п)положительны, поэтому, возведя их в квадрат, получим равносильное неравенство |xj-М(ξ)|2≥ε2. Воспользуемся этим замечанием и, заменяя в оставшейся сумме каждый из множителей |xj-М(ξ)|2 числом ε2 (при этом неравенство может лишь усилиться), получим D(ξ)≥ε2(pk+1+pk+2+...+рп). По теореме сложения, сумма вероятностей pk+1+pk+2+…+рп есть вероятность того, что ξ примет одно, безразлично какое, из значений xk+1,xk+2,..., xп, а при любом из них отклонение удовлетворяет неравенству |xj-М(ξ)|≥ε. Отсюда следует, что сумма pk+1+pk+2+...+рп выражает вероятность Р (| ξ - М (ξ)|≥ ε). Это соображение позволяет переписать соответствующее неравенство: D(ξ)≥ε2Р(|ξ-М(ξ)|≥ε), или Р(|ξ-М(ξ)|≥ε)≤D(ξ)/ε2. Окончательно получим Р(|ξ-М(ξ)|<ε)≥1-D(ξ)/ε2, что и требовалось доказать. Неравенство Чебышева имеет для практики ограниченное значение, поскольку часто дает грубую, а иногда и тривиальную (не представляющую интереса) оценку. Например, если D (ξ)> ε2 и, следовательно, D (ξ) /ε2>1, то 1- D (ξ) /ε2 <0; таким образом, в этом случае неравенство Чебышева указывает лишь на то, что вероятность отклонения неотрицательна, а это и без того очевидно, так как любая вероятность выражается неотрицательным числом. Теоретическое же значение неравенства Чебышева весьма велико. Теорема (Чебышева). Если ξ1, ξ2,..., ξn...- попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа С), то, как бы мало ни было положительное число ε, вероятность неравенства
будет как угодно близка к единице, если число случайных величин достаточно велико. Другими словами, в условиях теоремы
Таким образом, теорема Чебышева утверждает, что если рассматривается достаточно большое число независимых случайных величин, имеющих ограниченные дисперсии, то почти достоверным можно считать событие, состоящее в том, что отклонение среднего арифметического случайных величин от среднего арифметического их математических ожиданий будет по абсолютной величине сколь угодно малым. Доказательство. Введем в рассмотрение новую случайную величину - среднее арифметическое случайных величин
Найдем математическое ожидание M Применяя к величине P или, учитывая соотношение (1), P Пользуясь свойствами дисперсии (постоянный множитель можно вынести за знак дисперсии, возведя eго в квадрат; дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых), получим
По условию дисперсии всех случайных величин ограничены постоянным числом С, то есть имеют место неравенства: D (ξ1)≤ С; D (ξ2)≤ С,…, D (ξn)≤ С, поэтому (D (ξ1)+ D (ξ2)+…+ D (ξn))/ n2 ≤(C + C +…+ C)/ n2 = nC / n2 = C / n. Итак,
Подставляя правую часть (3) в неравенство (2) (отчего последнее может быть лишь усилено), имеем P Отсюда, переходя к пределу при п
Наконец, учитывая, что вероятность не может превышать единицу, окончательно можем написать
Теорема доказана. Формулируя теорему Чебышева, мы предполагали, что случайные величины имеют различные математические ожидания. На практике часто бывает, что случайные величины имеют одно и то же математическое ожидание. Очевидно, что если вновь допустить, что дисперсии этих величин ограничены, то к ним будет применима теорема Чебышева. Обозначим математическое ожидание каждой из случайных величин через а; в рассматриваемом случае среднее арифметическое математических ожиданий, как легко видеть, также равно а. Мы можем сформулировать теорему Чебышева для рассматриваемого частного случая. Если ξ1, ξ2,..., ξn...- попарно независимые случайные величины, имеющие одно и то же математическое ожидание а, и если дисперсии этих величин равномерно ограничены, то, как бы мало ни было число ε > 0, вероятность неравенства
будет как угодно близка к единице, если число случайных величин достаточно велико. Другими словами, в условиях теоремы будет иметь место равенство
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 473; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.251.22 (0.128 с.) |
 f2 (z - x) dx,
f2 (z - x) dx,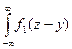 f2 (y) dy,
f2 (y) dy, f2 (z - x) dx,
f2 (z - x) dx, f2 (y) dy.
f2 (y) dy. e-x/3 (0≤ x <∞);
e-x/3 (0≤ x <∞); e-y/4 (0≤ y <∞).
e-y/4 (0≤ y <∞).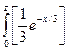
 dx =
dx =  e-z /4
e-z /4  dx = e-z / 4 (1- e-z /12).
dx = e-z / 4 (1- e-z /12). dz = 1.
dz = 1. p (yj | x).
p (yj | x). ψ (y | x) dy,
ψ (y | x) dy, p(yj|x1)=у1 р(у1|х1)+у2 р(у2|х1)=3 (1/3)+6 (2/3)=5.
p(yj|x1)=у1 р(у1|х1)+у2 р(у2|х1)=3 (1/3)+6 (2/3)=5.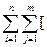 хi-М(ξ)] [yj-M(η)]р(хi,yj),
хi-М(ξ)] [yj-M(η)]р(хi,yj), [y-M(η)]f(x,y)dxdy.
[y-M(η)]f(x,y)dxdy. ].
].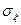
 ).
). =
= 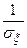 М[ξ-M(ξ)]=
М[ξ-M(ξ)]=  D[ξ-M(ξ)]=
D[ξ-M(ξ)]=  =1.
=1. = M
= M 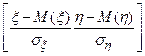 = M (ξ’η’)= cov(ξ',η’)
= M (ξ’η’)= cov(ξ',η’)

 -2
-2  , f2(у)=
, f2(у)=  внутри заданного эллипса и f1(x)=0, f2(y)=0 вне его.
внутри заданного эллипса и f1(x)=0, f2(y)=0 вне его. yf (x,y) dxdy.
yf (x,y) dxdy.
 dy.
dy. ×
× 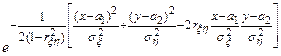 .
.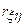 =0, получим
=0, получим ×
×  =
=


 = f1 (x) f2 (у).
= f1 (x) f2 (у).
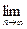 P
P  =1.
=1. =(ξ1+ξ2+...+ξn) /п
=(ξ1+ξ2+...+ξn) /п =
=  . (1)
. (1) ≥ 1-
≥ 1-  ,
, ≥1-
≥1-  =
=  .
. (3)
(3)
 ,получим
,получим
 = 1.
= 1.


