
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наиболее вероятное число успехов.Стр 1 из 11Следующая ⇒
Пример. 1). Точка с координатами 2). Точка с координатами
1. Рассмотрим х,у 2. На рисунке событие А заштриховано вертикальными линиями, событие В - горизонтальными. Видим, что Р(А)=3/4, Р(В)=3/4, Р(А Отметим, что если события А и В несовместны, то они независимы, если и только если Р(А)=0 или Р(В)=0. Из определения независимости и теоремы умножения следует справедливость следующих утверждений. Если Р(В)>0, то события А и В независимы тогда и только тогда, когда Р(А|В)=Р(А). Если Р(А)>0, то события А и В независимы тогда и только тогда, когда Р(В|А)=Р(В). Лемма. Если события А и В независимы, то независимы и события А и Доказательство. Так как А=A Определение. События А1,..., Ап называются независимыми в совокупности, если для любого набора 1 ≤ i1,..., ik ≤ n Р ( Замечание. Если события А1,..., Ап независимы в совокупности, то они попарно независимы, то есть любые два события Ai,Aj независимы. Достаточно в равенстве определения взять k=2. Обратное, как показывает следующий пример, неверно. Пример (С.Н. Бернштейна). Рассмотрим правильный тетраэдр, 3 грани которого окрашены, соответственно, в красный, синий, зеленый цвета, а четвертая грань содержит все три цвета. Событие А (В, С) означает, что выпала грань, содержащая красный (синий, зеленый) цвета. Вероятность каждого из этих событий равна 1/2, так как каждый цвет есть на двух гранях из четырех. Вероятность пересечения любых двух из них равна 1/4, так как только одна грань содержит два цвета. А так как 1/4=1/2·1/2, то все события попарно независимы. Но вероятность пересечения всех трех тоже равна 1/4, а не 1/8, то есть события не являются независимыми в совокупности. Получили, что равенство определения 3 выполнено для k=2, но не выполнено для k=3.
§9. Формула полной вероятности. Формула Байеса
Пример. Есть 3 завода, производящие одну и ту же продукцию. При этом 1 -й завод производит 25%, 2 -й завод - 35% и 3 -й завод - 40% всей производимой продукции. Брак составляет 5% от продукции 1 -го завода, 3% от продукции 2 -го и 4% от продукции 3 -го завода. Вся продукция смешивается и поступает в продажу. Найти а) вероятность купить бракованное изделие; б) условную вероятность того, что купленное изделие изготовлено 1 -м заводом, если это изделие бракованное. Первая вероятность равна доле бракованных изделий в объеме всей продукции, то есть 0,05∙0,25+0,03∙0,35+0,04∙0,4. Вторая вероятность равна доле брака 1-го завода среди всего брака, то есть
Определение. Набор попарно несовместных событий H1, H2,...таких, что P (Hi)>0 для всех i и События H1,H2,... образующие полную группу событий, часто называют гипотезами. При подходящем выборе гипотез для произвольного события А могут быть сравнительно просто вычислены Р(А|Hi) (вероятность событию А произойти при выполнении «гипотезы» Hi) и собственно Р (Hi) (вероятность выполнения «гипотезы» Hi).Как, используя эти данные, посчитать вероятность события А? Теорема (Формула полной вероятности). Пусть H1, H2,... – полная группа событий. Тогда вероятность любого события А может быть вычислена по формуле: Р (А)= Доказательство.Заметим, что А=А Р (А)=
Теорема (Формула Байеса). Пусть H1, H2,... - полная группа событий и А – некоторое событие положительной вероятности. Тогда условная вероятность того, что имело место событие Нk, если в результате эксперимента наблюдалось событие А, может быть вычислена по формуле: Р (Нk | А)= Доказательство.По определению условной вероятности, Р (Нk | А)= Последнее равенство следует из теоремы умножения и формулы полной вероятности. Пример. Вернемся к предыдущему примеру. Изделие выбирается наудачу из всей произведенной продукции. Рассмотрим три гипотезы: Hi ={ изделие изготовлено i-м заводом }, i=1,2,3. Вероятности этих событий даны: P(H1)=0,25, Р(H2)=0,35, Р(H3)=0,4. Пусть А ={ изделие оказалось бракованным }. Даны также условные вероятности Р(А|Н1)=0,05, Р(А|Н2)=0,03, Р(А|Н3)=0,04.
Пример. Два стрелка подбрасывают монетку и выбирают, кто из них стреляет по мишени (одной пулей). Первый стрелок попадает по мишени с вероятностью 1, второй стрелок - с вероятностью 0,00001. Можно сделать два предположения об эксперименте: H1 ={ стреляет 1-й стрелок } и H2 ={ стреляет 2-й стрелок }. Априорные (a’priori — «до опыта») вероятности этих гипотез одинаковы: Р(Н1)=Р(H2)=1/2. Рассмотрим событие А ={ пуля попала в мишень }. Известно, что Р(А|Н1)=1, Р(А|H2)=0,00001. Поэтому вероятность пуле попасть в мишень Р(А)=1/2∙1+1/2∙0.00001. Предположим, что событие А произошло. Какова теперь апостериорная (a’posteriori - «после опыта») вероятность каждой из гипотез Hi? Очевидно, что первая из этих гипотез много вероятнее второй (а именно, в 100000 раз). Действительно, Р (А | Н1)=
Р (А | H2)=
§10. Схема Бернулли
Определение. Схемой Бернулли называется последовательность независимых испытаний, в каждом из которых возможны лишь два исхода - «успех» и «неудача», при этом «успех» в одном испытании происходит с вероятностью р Теорема (Формула Бернулли). Обозначим через P ( Доказательство.Событие А ={ Другие благоприятствующие событию А элементарные исходы отличаются от рассмотренного выше лишь расположением k успехов на п местах. Есть ровно C
Биномиальное распределение.
Пусть производится п независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна р (следовательно, вероятность непоявления q=1-р). Рассмотрим в качестве дискретной случайной величины ξ число появлений события А в этих испытаниях. Найдем закон распределения величины ξ. Для этого требуется определить возможные значения ξ и их вероятности. Очевидно, событие А в п испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза,..., либо п раз. Таким образом, возможные значения ξ таковы: x1=0,x2=1,x3=2,...,xn+1=п. Остается найти вероятности этих возможных значений, для чего достаточно воспользоваться формулой Бернулли: Pn (k)= С где k=0,1,2,...,п. Эта формула является аналитическим выражением искомого закона распределения. Определение. Случайная величина имеет Биномиальное распределение если ее распределение вероятностей задается формулой P (ξ=k)= С
Закон назван «биномиальным» потому, что правую часть формулы можно рассматривать как общий член разложения бинома Ньютона: (p + q) n = С Таким образом, первый член разложения рп определяет вероятность наступления рассматриваемого события п раз в п независимых испытаниях; второй член npn-1q определяет вероятность наступления события п - 1 раз;...; последний член qn определяет вероятность того, что событие не появится ни разу. Напишем биномиальный закон в виде таблицы:
Пример. Монета брошена 2 раза. Написать в виде таблицы закон распределения случайной величины ξ - числа выпадений «герба». Решение. Вероятность появления «герба» в каждом бросании монеты р=1/2, следовательно, вероятность непоявления «герба» q=1-1/2=1/2. При двух бросаниях монеты «герб» может появиться либо 2 раза, либо 1 раз, либо совсем не появиться. Таким образом, возможные значения ξ таковы: x1=2,x2=1,x3=0. Найдем вероятности этих возможных значений по формуле Бернулли: P2(2)=С P2(1)=С P2(0)=С Напишем искомый закон распределения:
Контроль: 0,25 + 0,5 + 0,25=1.
Распределение Пуассона.
Определение. Случайная величина имеет распределение Пуассона если ее распределение вероятностей задается формулой
P (ξ=k)= Эта формула выражает закон распределения Пуассона для вероятностей редких событий. Она используется для приблизительных вычислений в схеме Бернулли, когда n велико, р мало Имеются специальные таблицы, пользуясь которыми можно найти эти вероятности,зная k и Пример. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия. Решение. По условию, п=5000, р=0,0002, k=3. Найдем
По формуле Пуассона искомая вероятность приближенно равна Р5000(3)=
Нормальная кривая. Определение. График плотности нормального распределения называют нормальной кривой (кривой Гаусса). Исследуем функцию y = методами дифференциального исчисления.
Свойства нормальной кривой. Свойство 1. Очевидно, функция определена на всей оси x. Свойство 2. При всех значениях х функция принимает положительные значения, то есть нормальная кривая расположена над осью OX.
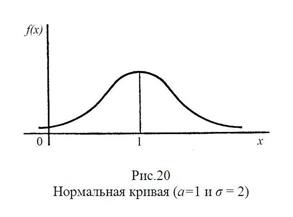
Свойство 3 Предел функции при неограниченном возрастании х (по абсолютной величине) равен нулю: Свойство 4. Исследуем функцию на экстремум. Найдем первую производную: y ´= Легко видеть, что у’ = 0 при х=а, у’ > 0 при х < а, у’ < 0 при х > а. Следовательно, при х=а функция имеет максимум, равный 1 /(σ Свойство 5. Разность х - а содержится в аналитическом выражении функции в квадрате, то есть график функции симметричен относительно прямой х = а. Свойство 6. Исследуем функцию на точки перегиба. Найдем вторую производную: y ´´= Легко видеть, что при х=а+σ и х=а - σ вторая производная равна нулю, а при переходе через эти точки она меняет знак (в обеих этих точках значение функции равно 1 /(σ Изобразим нормальную кривую при а=1 и σ=2.
Правило трех сигм.
Преобразуем формулу Р(|ξ–а|<δ)=2Ф(δ/σ), положив δ=σt. В итоге получим Р(|ξ–а|<σt)=2Ф(t), Если t = 3 и, следовательно, σt=3σ, то Р(|ξ–а|<3σ)=2Ф(3)=2·0,49865=0,9973, то есть вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973. Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0,0027. Это означает, что лишь в 0,27% случаев так может произойти. Такие события исходя из принципа невозможности маловероятных событий можно считать практически невозможными. В этом и состоит сущность правила трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения. На практике правило трех сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.
§27. Функции случайных величин
Определение. Если каждому возможному значению случайной величины ξ соответствует одно возможное значение случайной величины η, то η называют функцией случайного аргумента ξ: η = φ (ξ). Далее показано, как найти распределение функции по известному распределению дискретного и непрерывного аргумента. 1. Пусть аргумент ξ - дискретная случайная величина. а) Если различным возможным значениям аргумента ξ соответствуют различные возможные значения функции η, то вероятности соответствующих значений ξ и η между собой равны. Пример. Дискретная случайная величина ξ задана распределением
Найти распределение функции η=ξ2. Решение. Найдем возможные значения η: у1=22=4;у2=32=9. Напишем искомое распределение η:
б) Если различным возможным значениям ξ соответствуют значения η, среди которых есть равные между собой, то следует складывать вероятности повторяющихся значений η. 2. Пусть аргумент ξ - непрерывная случайная величина. Найдем распределение функции η = φ (ξ), зная плотность распределения случайного аргумента ξ. Доказано: если у = φ (х) - дифференцируемая строго возрастающая или строго убывающая функция, обратная функция которой х=ψ (у), то плотность распределения g (y) случайной величины η находится с помощью равенства g(y)=f[ψ(у)] |ψ´(у)|. Пример. Случайная величина ξ распределена нормально, причем ее математическое ожидание а = 0. Найти распределение функции η=ξ3. Решение. Так как функция у = х3 дифференцируема и строго возрастает, то можно применить формулу g(y)=f[ψ(у)] |ψ´(у)|. Найдем функцию, обратную функции у = х3: ψ (у) =х = y1/3. Найдем f[ψ(у)]. По условию, f (x)= поэтому f[ψ(у)]=f[y1/3]= Найдем производную обратной функции по у: ψ ´(у)=(y1/3)´= Найдем искомую плотность распределения: g (y)= Пользуясь данным соотношением можно доказать, что линейная функция η=Aξ+B нормально распределенного аргумента ξ также распределена нормально, причем для того чтобы найти математическое ожидание η, надо в выражение функции подставить вместо аргумента ξ его математическое ожидание а: М(η)=Аа+В; для того чтобы найти среднее квадратическое отклонение η, надо среднее квадратическое отклонение аргумента ξ умножить на модуль коэффициента при ξ: σ(η)=|A|σ(ξ).
Равенство Маркова.
Обозначим через Рij (п) вероятность того, что в результате п шагов (испытаний) система перейдет из состояния i в состояние j. Например, Р25 (10) - вероятность перехода за 10 шагов из второго состояния в пятое. Подчеркнем, что при п = 1 получим переходные вероятности Рij (1)= pij. Поставим перед собой задачу: зная переходные вероятности pij,найти вероятности Рij (п) перехода системы из состояния i в состояние j за п шагов. С этой целью введем в рассмотрение промежуточное (между i и j) состояние r. Другими словами, будем считать, что из первоначального состояния i за т шагов система перейдет в промежуточное состояние r с вероятностью Pir (m), после чего за оставшиеся п - т шагов из промежуточного состояния r она перейдет в конечное состояние j с вероятностью Prj (n-т). По формуле полной вероятности, Рij (п)= Эту формулу называют равенством Маркова (также данное соотношение называют формулой Чепмена-Колмогорова). Пояснение. Введем обозначения: А - интересующее нас событие (за п шагов система перейдет из начального состояния i в конечное состояние j), следовательно, Р (А)= Рij (п); Вr (r=1,2,...,k)- гипотезы (за т шагов система перейдет из первоначального состояния i в промежуточное состояние r), следовательно, Р (Br)= Pir (m); P По формуле полной вероятности, Р (А)= или в принятых нами обозначениях Pij (n)=
Покажем, что, зная все переходные вероятности pij = Рij (1), т. е. зная матрицу P1 перехода из состояния в состояние за один шаг, можно найти вероятности Рij(2) перехода из состояния в состояние за два шага, следовательно, и саму матрицу перехода P2; по известной матрице P2 можно найти матрицу P3 перехода из состояния в состояние за 3 шага, и т. д. Действительно, положив n=2, т =1в равенстве Маркова Pij (n)= получим Pij(2) = или Pij(2)= Таким образом, можно найти все вероятности Р ij(2), следовательно, и саму матрицу P2. Напишем полученное соотношение в матричной форме: P2=P1P1=P Положив п=3, т=2 аналогично получим P3=P1P2=P1P В общем случае Pn=P Пример. Задана матрица перехода P1= Решение. Воспользуемся формулой P2=P P2= Перемножив матрицы, окончательно получим P2=
Пример. 1). Точка с координатами 2). Точка с координатами
1. Рассмотрим х,у 2. На рисунке событие А заштриховано вертикальными линиями, событие В - горизонтальными. Видим, что Р(А)=3/4, Р(В)=3/4, Р(А Отметим, что если события А и В несовместны, то они независимы, если и только если Р(А)=0 или Р(В)=0. Из определения независимости и теоремы умножения следует справедливость следующих утверждений. Если Р(В)>0, то события А и В независимы тогда и только тогда, когда Р(А|В)=Р(А). Если Р(А)>0, то события А и В независимы тогда и только тогда, когда Р(В|А)=Р(В). Лемма. Если события А и В независимы, то независимы и события А и Доказательство. Так как А=A Определение. События А1,..., Ап называются независимыми в совокупности, если для любого набора 1 ≤ i1,..., ik ≤ n Р ( Замечание. Если события А1,..., Ап независимы в совокупности, то они попарно независимы, то есть любые два события Ai,Aj независимы. Достаточно в равенстве определения взять k=2. Обратное, как показывает следующий пример, неверно. Пример (С.Н. Бернштейна). Рассмотрим правильный тетраэдр, 3 грани которого окрашены, соответственно, в красный, синий, зеленый цвета, а четвертая грань содержит все три цвета. Событие А (В, С) означает, что выпала грань, содержащая красный (синий, зеленый) цвета. Вероятность каждого из этих событий равна 1/2, так как каждый цвет есть на двух гранях из четырех. Вероятность пересечения любых двух из них равна 1/4, так как только одна грань содержит два цвета. А так как 1/4=1/2·1/2, то все события попарно независимы. Но вероятность пересечения всех трех тоже равна 1/4, а не 1/8, то есть события не являются независимыми в совокупности. Получили, что равенство определения 3 выполнено для k=2, но не выполнено для k=3.
§9. Формула полной вероятности. Формула Байеса
Пример. Есть 3 завода, производящие одну и ту же продукцию. При этом 1 -й завод производит 25%, 2 -й завод - 35% и 3 -й завод - 40% всей производимой продукции. Брак составляет 5% от продукции 1 -го завода, 3% от продукции 2 -го и 4% от продукции 3 -го завода. Вся продукция смешивается и поступает в продажу. Найти а) вероятность купить бракованное изделие; б) условную вероятность того, что купленное изделие изготовлено 1 -м заводом, если это изделие бракованное. Первая вероятность равна доле бракованных изделий в объеме всей продукции, то есть 0,05∙0,25+0,03∙0,35+0,04∙0,4. Вторая вероятность равна доле брака 1-го завода среди всего брака, то есть
Определение. Набор попарно несовместных событий H1, H2,...таких, что P (Hi)>0 для всех i и События H1,H2,... образующие полную группу событий, часто называют гипотезами. При подходящем выборе гипотез для произвольного события А могут быть сравнительно просто вычислены Р(А|Hi) (вероятность событию А произойти при выполнении «гипотезы» Hi) и собственно Р (Hi) (вероятность выполнения «гипотезы» Hi).Как, используя эти данные, посчитать вероятность события А? Теорема (Формула полной вероятности). Пусть H1, H2,... – полная группа событий. Тогда вероятность любого события А может быть вычислена по формуле: Р (А)= Доказательство.Заметим, что А=А Р (А)=
Теорема (Формула Байеса). Пусть H1, H2,... - полная группа событий и А – некоторое событие положительной вероятности. Тогда условная вероятность того, что имело место событие Нk, если в результате эксперимента наблюдалось событие А, может быть вычислена по формуле: Р (Нk | А)= Доказательство.По определению условной вероятности, Р (Нk | А)= Последнее равенство следует из теоремы умножения и формулы полной вероятности. Пример. Вернемся к предыдущему примеру. Изделие выбирается наудачу из всей произведенной продукции. Рассмотрим три гипотезы: Hi ={ изделие изготовлено i-м заводом }, i=1,2,3. Вероятности этих событий даны: P(H1)=0,25, Р(H2)=0,35, Р(H3)=0,4. Пусть А ={ изделие оказалось бракованным }. Даны также условные вероятности Р(А|Н1)=0,05, Р(А|Н2)=0,03, Р(А|Н3)=0,04. Пример. Два стрелка подбрасывают монетку и выбирают, кто из них стреляет по мишени (одной пулей). Первый стрелок попадает по мишени с вероятностью 1, второй стрелок - с вероятностью 0,00001. Можно сделать два предположения об эксперименте: H1 ={ стреляет 1-й стрелок } и H2 ={ стреляет 2-й стрелок }. Априорные (a’priori — «до опыта») вероятности этих гипотез одинаковы: Р(Н1)=Р(H2)=1/2. Рассмотрим событие А ={ пуля попала в мишень }. Известно, что Р(А|Н1)=1, Р(А|H2)=0,00001.
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 328; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.151.231 (0.243 с.) |
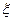 ,
, 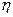 бросается наудачу в квадрат со стороной 1. Доказать, что для любых x, у
бросается наудачу в квадрат со стороной 1. Доказать, что для любых x, у  R события А ={
R события А ={ 

 В)=ху, так что события А={
В)=ху, так что события А={  ,
,  и В,
и В,  А
А 
 )= Р (
)= Р ( .
. = Ω, называется полной группой событий или разбиением пространства Ω.
= Ω, называется полной группой событий или разбиением пространства Ω. .
. =
= 
 -аддитивность вероятностной меры, а во втором — теорему умножения)
-аддитивность вероятностной меры, а во втором — теорему умножения) =
=  .
. =
=  =
=  ;
; =
=  .
. число успехов в n испытаниях схемы Бернулли. Тогда для любого k=0, 1, …, n
число успехов в n испытаниях схемы Бернулли. Тогда для любого k=0, 1, …, n pk (1- p) n-k = C
pk (1- p) n-k = C  . Здесь буквами «у» и «н» обозначены, соответственно, успешный и неудачный результаты испытаний. Поскольку испытания независимы, вероятность такого элементарного исхода (первые k испытаний завершились успехом, остальные неудачей) равна pk (1- p) n-k.
. Здесь буквами «у» и «н» обозначены, соответственно, успешный и неудачный результаты испытаний. Поскольку испытания независимы, вероятность такого элементарного исхода (первые k испытаний завершились успехом, остальные неудачей) равна pk (1- p) n-k. pn + С
pn + С  pn-1q +…+ С
pn-1q +…+ С  qn.
qn. p2=(1/2)2=0,25,
p2=(1/2)2=0,25, pq=2·(1/2) (1/2) =0,5,
pq=2·(1/2) (1/2) =0,5, q2=(1/2)2=0,25.
q2=(1/2)2=0,25.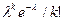 , k=0,1,2,...
, k=0,1,2,... .
.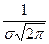 e
e 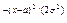
 y=0,то есть ось OX служит горизонтальной асимптотой графика.
y=0,то есть ось OX служит горизонтальной асимптотой графика.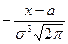 e
e 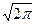 ).
).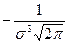 e
e  .
.
 ,
,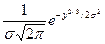 .
.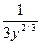 .
.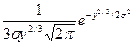 .
.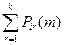 Prj (n-т).
Prj (n-т). (A)- условная вероятность наступления А при условии, что имела место гипотеза Вr (за п - т шагов система перейдет из промежуточного состояния r в конечное состояние j), следовательно, P
(A)- условная вероятность наступления А при условии, что имела место гипотеза Вr (за п - т шагов система перейдет из промежуточного состояния r в конечное состояние j), следовательно, P  P
P  Prj(2-1),
Prj(2-1),
 .
. .
. .
. . Найти матрицу перехода P2=
. Найти матрицу перехода P2=  .
. .
.


