Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плоскостью общего положения называется плоскость, случайным образом расположенная в пространстве, т.е. имеющая произвольные углы наклона к плоскостям проекций.Содержание книги
Поиск на нашем сайте Примеры плоскостей общего положения были рассмотрены выше. Плоскостью частного положения называется плоскость, параллельная или перпендикулярная плоскости проекций. Плоскости частного положения бывают двух видов: 1. плоскости уровня; 2. проецирующие плоскости.
Плоскости частного положения.
1. Горизонтальная плоскость уровня – плоскость параллельная горизонтальной пл. проекций a || p1 D A¢B¢C¢ @ D ABC
Любая прямая или фигура, принадлежащая плоскости a проецируется на пл. пр. p1 в натуральную величину. По отношению к пл. пр. p2 плоскость a перпендикулярна и поэтому вся плоскость a спроецируется на пл. p2 в прямую линию, параллельную оси x. Эту линию можно назвать следом плоскости a - ap2. След плоскости - это линия пересечения плоскости с плоскостью проекций.
Горизонтальная плоскость уровня может быть задана одной линией - - фронтальным следом ap2 (рис.3.5):
a (ap2) или a (a ¢¢)
b || p2 D A¢¢B¢¢C¢¢ @ D ABC
bp2 - горизонтальный след плоскости b. Плоскость может быть задана следом b (bp2) или (b¢)
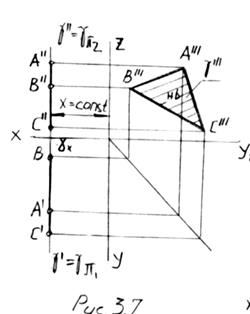
3. Профильная плоскость уровня - плоскость, параллельная профильной пл. пр. p3 (рис.3.7) gp2 - фронтальный след пл. g. gp2 - горизонтальный след пл. g. gx - точка схода следов пл. g. D A¢¢¢B¢¢¢C¢¢¢ @ D ABC.
3.3.2.Плоскости проецирующие - плоскости, перпендикулярные к одной из плоскостей проекций.
Плоскости уровня являются двоякопроецирующими (перпендикулярными сразу к двум плоскостям проекций).
Рис.3.8
1. Горизонтально – проецирующая пл. - плоскость, перпендикулярная горизонтальной плоскости пр. p1 (рис.3.8). a ^ p1 Ðb° - угол наклона пл. a к пл. пр. p2.
Горизонтально - проецирующая плоскость проецируется на пл. p1 в прямую линию a¢ = ap1 ap1 - горизонтальный след пл. a.
Фронтально - проецирующая плоскость - плоскость, перпен - дикулярная к фронтальной плоскости проекций p2 (рис.3.9) b ^ p2 Ð a° - угол наклона пл. b к плоскости проекций p1.
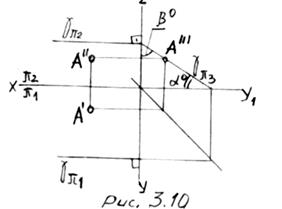
3. Профильно - проецирующая плоскость - плоскость, перпен- дикулярная к профильной пл. пр. p3 (рис.3.10) g ^ p3
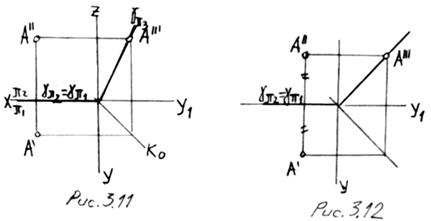
Профильно - проецирующая плоскость может быть осевой (проходить через ось, рис.3.11).
Частный случай осевой плоскости - биссекторная плоскость, все точки которой равноудалены от пл. пр. p1 и p2 (рис.3.12).
3.4. Главные линии плоскости (линии уровня).
Линиями уровня плоскости называют-ся линии, принадлежащие плоскости и параллельные одной из плоскостей проек-ций. К таким линиям относятся горизонталь, фронталь и профильная прямая уровня. Горизонталь – h (h¢,h¢¢) (рис.3.13),
h || p1, hÌ { a ( D ABC)}
Построение горизонтали в плос- кости всегда надо начинать с фронтальной проекции, т.к. известно, что если прямая параллельна горизонтальной пл. пр. p1, то её фронтальная проекция всегда параллельна оси x. h || p1 Þ h || x
|
|||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 497; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.005 с.) |

 3.3.1. Плоскости уровня - плоскости, параллельные одной из плоскостей проекций (рис.3.4).
3.3.1. Плоскости уровня - плоскости, параллельные одной из плоскостей проекций (рис.3.4).
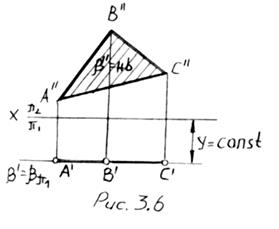 2. Фронтальная плоскость уровня – плоскость, параллельная фронталь- ной плоскости проекций p2 (рис.3.6):
2. Фронтальная плоскость уровня – плоскость, параллельная фронталь- ной плоскости проекций p2 (рис.3.6):