
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление интегралов Стилтьеса
Докажем следующую теорему: Если функция
где функция
Интеграл справа существует. Существование интеграла Стилтьеса при сделанных предположениях уже было доказано (п.3,3). Остается лишь установить равенство (11). Без умаления общности можно предположить функцию Составим, как обычно, сумму Стилтьеса
Так как, с другой стороны, можно написать
то будем иметь
Очевидно, для
Но мы уже знаем (п.3,3), что при
что и доказывает формулу (11). В частности, из доказанной теоремы вытекает (если учесть замечание в п.3) такое следствие, удобное для непосредственного применения на практике: 2. При прежних предположениях относительно функции
Интересно отметить, что интеграл справа в формуле (12) формально получается из интеграла слева, если, понимая символ Обращаясь к случаям, когда функция
Она имеет разрыв первого рода - скачок - в точке Предположим, что функция Составим сумму Стилтьеса:
Пусть точка
Аналогично можно убедиться в том, что (при
(при Теперь мы в состоянии доказать теорему, в некотором смысле более общую, чем 2, а
именно, отказаться от требования непрерывности функции: Пусть функция
терпит разрыв первого рода. Тогда существует интеграл Стилтьеса и выражается формулой
Характерно здесь наличие внеинтегральной суммы, где фигурируют скачки функции Для упрощения записи введем обозначения для скачков функции
очевидно, для
Составим вспомогательную функцию:
которая как бы вбирает в себя все разрывы функции Для значений
Аналогично проверяется и непрерывность функции Далее, если взять точку
Для непрерывной функции
Точно так же легко вычислить и интеграл
Складывая почленно эти два равенства, мы и придем к равенству (15); существование интеграла Стилтьеса от Примеры Вычислить по формуле (11) интегралы: а) б) в) Решение: а) б)
в) Вычислить по формуле (15) интегралы: а) б) Решение: а) Функция
б) Скачок 1 при Имеем:
Вычислить по формуле (15) интегралы: а) где
Решение: Функция
Поэтому а) Аналогично, б) в) Предположим, что вдоль отрезка Разобьем промежуток
На отрезке
При стремлении к 0 всех
Можно было бы здесь сначала установить "элементарный" статический момент Аналогично для момента инерции
Важно подчеркнуть, что интеграл Стилтьеса дал возможность объединить одной интегральной формулой разнородные случаи непрерывно распределенных интеграл сосредоточенных масс! Пусть непрерывно распределенные массы имеют линейную плотность
В каждой же точке Если теперь разложить интеграл (16) по формуле (15), то получим
Всмотревшись в правую часть, легко в первом члене узнать статический момент непрерывно распределенных масс, а во втором - статический момент сосредоточенных масс. Аналогичный результат получится интеграл для интеграла (17). а) Составить выражение Решение:
В промежутке
б) То же самое - для такого распределения: массы величины 2 при Решение:
В промежутке
в) выяснить распределение масс, если Решение: Массы величины 1 в точках
6. Рассмотрим другой вопрос, в котором интеграл Стилтьеса играет такую же роль, как интеграл в упражнении 4). Предположим, что на балку (рис) покоящуюся на двух опорах, кроме непрерывно распределенной нагрузки действуют и сосредоточенные силы. Расположим ось Поставим задачей определить так называемый изгибающий момент
Так как на элементе
то, "суммируя" получим
Аналогично, исходя из левой части балки, можно было бы получить (учитывая изменение положительного направления для отсчета моментов)
Легко непосредственно усмотреть, что оба выражения изгибающего момента в действительности тождественны. Их равенство равносильно условию
которое является следствием из условий равновесия
выражающих равенство нулю суммы всех сил интеграл суммы моментов (относительно начала) всех сил, действующих на балку. Если интенсивность непрерывно распределенной нагрузки обозначить через
Пусть сосредоточенные силы
В двух слагаемых правой части легко узнать моменты, порожденные порознь непрерывной нагрузкой интеграл сосредоточенными силами: интеграл Стилтьеса охватывает их единой интегральной формулой. Установим ещё один факт, интересный для теории сопротивления материалов. Произведя в формуле (18) интегрирование по частям, получим
Отсюда ясно, что всюду, за исключением точек приложения сосредоточенных сил, имеет место равенство
Пусть балка длины Решение: Формула (15) может оказаться полезной интеграл для вычисления обычных интегралов (в смысле Римана). Проиллюстрируем это на следующем примере. Пусть
так, что в каждой из частей функция Пусть, далее,
Тогда имеет место следующая формула:
Действительно, последовательно находим
двойная подстановка исчезает, а интеграл
width="288" height="51" border="0" /> Аналогично
и т.д. Установим в заключение, с помощью формулы (11) одно полезное обобщение формулы интегрирования по частям для обыкновенных интегралов. Именно, если
то справедлива формула
Для доказательства, по формуле (11) заменим интеграл слева интегралом Стилтьеса интеграл проинтегрируем по частям (п.5):
Остается ещё раз применить формулу (11) к последнему интегралу, чтобы прийти к (19). Здесь функции
Геометрическая иллюстрация интеграла Стилтьеса
Рассмотрим интеграл
предполагая функцию Система параметрических уравнений
выражает некоторую кривую
отвечающие всем скачкам функции С этой целью разложим промежуток на части точками
и в соответствии с этим промежуток
Введя наименьшее и наибольшее значения
Легко видеть теперь, что они представляют площади фигур, составленных из входящих интеграл из выходящих прямоугольников, между которыми содержится рассматриваемая криволинейная фигура. Так как при стремлении к 0 всех Теорема о среднем, оценки Пусть в промежутке
а
Это и есть теорема о среднем для интегралов Стилтьеса. Для доказательства будем исходить из очевидных неравенств для стилтьесовской суммы
Переходя к пределу, получим
Или
Обозначая написанное отношение через Если функция
В практике интегралов Стилтьеса наиболее важным является случай, когда функция
Где
Действительно, для суммы Стилтьеса
так что остается лишь перейти к пределу, чтобы получить требуемое неравенство. Отсюда вытекает, в частности, и оценка близости суммы
и почленно вычитая эти равенства, получим
Если, как обычно, обозначить через
то, применяя оценку (25) к каждому интегралу
Если промежуток
Эти оценки будут нами использованы в следующем пункте.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 1635; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.222.47 (0.138 с.) |
 интегрируема в смысле Римана в промежутке
интегрируема в смысле Римана в промежутке  , а
, а  представлена интегралом
представлена интегралом
 абсолютно интегрируема в
абсолютно интегрируема в  (11)
(11) положительной.
положительной.


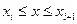 будет
будет  , где
, где  означает колебание функции
означает колебание функции  . Отсюда вытекает такая оценка написанной выше разности:
. Отсюда вытекает такая оценка написанной выше разности:
 последняя сумма стремится к 0, следовательно,
последняя сумма стремится к 0, следовательно,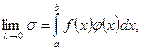
 , которая в
, которая в  (12)
(12) буквально как дифференциал, заменит его выражением
буквально как дифференциал, заменит его выражением  .
. , определяемой равенствами
, определяемой равенствами
 справа, причем величина скачка
справа, причем величина скачка  равна 1; в точке
равна 1; в точке  будет иметь такой же разрыв в точке
будет иметь такой же разрыв в точке  справа; наоборот,
справа; наоборот,  будет иметь подобный разрыв в точке
будет иметь подобный разрыв в точке  где
где  (при
(при 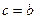 этот интеграл равен нулю).
этот интеграл равен нулю).
 попадет, скажем, в
попадет, скажем, в  -й промежуток, так что
-й промежуток, так что  . Тогда
. Тогда  , а при
, а при  , очевидно,
, очевидно,  . Таким образом, вся сумма
. Таким образом, вся сумма 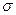 сводится к одному слагаемому:
сводится к одному слагаемому:  Пусть теперь
Пусть теперь  . Следовательно, существует (при
. Следовательно, существует (при 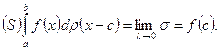 (13)
(13)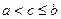 )
) (14)
(14) этот интеграл обращается в нуль).
этот интеграл обращается в нуль).
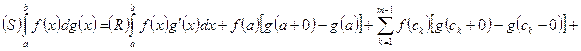
 (15)
(15) или
или  - односторонние.
- односторонние.


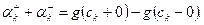

 , как мы сейчас установим, оказывается уже непрерывной.
, как мы сейчас установим, оказывается уже непрерывной. , отличных от всех
, отличных от всех  , непрерывность функции
, непрерывность функции  не вызывает сомнений, ибо для этих значений непрерывны обе функции
не вызывает сомнений, ибо для этих значений непрерывны обе функции  . Докажем теперь непрерывность
. Докажем теперь непрерывность  справа. Все слагаемые суммы
справа. Все слагаемые суммы  , непрерывны при
, непрерывны при  справа; поэтому достаточно изучить поведение выражения
справа; поэтому достаточно изучить поведение выражения 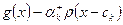 . При
. При  ; но таков же и его предел при
; но таков же и его предел при  :
: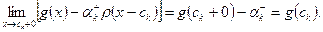
 слева.
слева. .
. , по предыдущей теореме, существует интеграл Стилтьеса
, по предыдущей теореме, существует интеграл Стилтьеса


 устанавливается попутно (п.4,3).
устанавливается попутно (п.4,3).
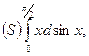




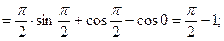

 где
где 
 где
где 
 и скачок - 2 при
и скачок - 2 при  ; в остальных точках
; в остальных точках  . Поэтому
. Поэтому
 и - 2 при
и - 2 при  (значение функции
(значение функции  при
при 
 б)
б)  в)
в) 





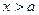 через
через  сумму всех масс, расположенных в промежутке
сумму всех масс, расположенных в промежутке  ; сверх того, положим,
; сверх того, положим,  . Очевидно,
. Очевидно, 
 содержится, очевидно, масса
содержится, очевидно, масса  . Точно так же на отрезке
. Точно так же на отрезке  содержится масса
содержится масса  . Считая массу во всех случаях сосредоточенной, например, на правом конце промежутка, получим для искомого статического момента приближенной выражение
. Считая массу во всех случаях сосредоточенной, например, на правом конце промежутка, получим для искомого статического момента приближенной выражение .
. , в пределе придем к точному результату:
, в пределе придем к точному результату: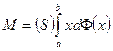 . (16)
. (16) , отвечающий отрезку оси от
, отвечающий отрезку оси от  , а затем "просуммировать" эти элементы.
, а затем "просуммировать" эти элементы. тех же масс относительно начал найдем формулу
тех же масс относительно начал найдем формулу (17)
(17) расположены сосредоточенные массы
расположены сосредоточенные массы  . Тогда, исключая эти точки, функция
. Тогда, исключая эти точки, функция 
 функция испытывает скачок, равный именно массе
функция испытывает скачок, равный именно массе  , в этой точке сосредоточенной.
, в этой точке сосредоточенной.
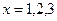 и непрерывно распределенные массы с плотностью 2 в промежутке
и непрерывно распределенные массы с плотностью 2 в промежутке  .
.
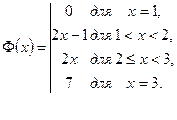
 в промежутке
в промежутке  .
.

 непрерывно распределенные массы с плотностью 1, в промежутке
непрерывно распределенные массы с плотностью 1, в промежутке  - массы с плотностью
- массы с плотностью 
 вертикально вниз (см. рис) Не делая различий между действующими силами, обозначим для
вертикально вниз (см. рис) Не делая различий между действующими силами, обозначим для  через
через  сумму всех сил, приложенных на отрезке
сумму всех сил, приложенных на отрезке  балки, включая интеграл реакции опор; далее, пусть
балки, включая интеграл реакции опор; далее, пусть  . Силу
. Силу  в произвольном сечении
в произвольном сечении  балки. Под этим разумеют сумму моментов всех сил, действующих на правую (или на левую) часть балки, относительно этого сечения. При этом, когда речь идет о правой части балки, момент считают положительным, если он вращает эту часть по часовой стрелке (для левой части - обратное правило).
балки. Под этим разумеют сумму моментов всех сил, действующих на правую (или на левую) часть балки, относительно этого сечения. При этом, когда речь идет о правой части балки, момент считают положительным, если он вращает эту часть по часовой стрелке (для левой части - обратное правило). , скажем, правой части балки приложена сила
, скажем, правой части балки приложена сила  , создающая элементарный момент
, создающая элементарный момент



 , то, исключая точки, где приложены сосредоточенные силы, будет
, то, исключая точки, где приложены сосредоточенные силы, будет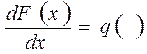
 приложены в точках
приложены в точках  . Тогда, очевидно, перерезывающее усилие именно в этих точках имеет скачки, соответственные равные
. Тогда, очевидно, перерезывающее усилие именно в этих точках имеет скачки, соответственные равные  . Далее, применяя, например, к интегралу (18) формулу (15), получим
. Далее, применяя, например, к интегралу (18) формулу (15), получим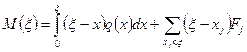 .
.


 несет "треугольную" нагрузку с интенсивностью
несет "треугольную" нагрузку с интенсивностью  ; кроме того, пусть к ней приложены сосредоточенная сила, равная 3, в точке
; кроме того, пусть к ней приложены сосредоточенная сила, равная 3, в точке  , интеграл реакции опор, обе равные - 3 (они устанавливаются по закону рычага). Определить перерезывающее усилие
, интеграл реакции опор, обе равные - 3 (они устанавливаются по закону рычага). Определить перерезывающее усилие  .
.
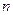 -й степени. Заменив значения функции
-й степени. Заменив значения функции  величину скачка
величину скачка 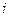 -й производной
-й производной  в
в  -й точке
-й точке  .
. и, вообще,
и, вообще, 

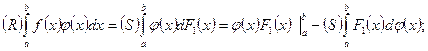
 <="" div="">
<="" div="">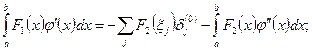
 и
и  обе абсолютно интегрируемы в промежутке
обе абсолютно интегрируемы в промежутке  и
и  определяются интегральными формулами:
определяются интегральными формулами:

 (19)
(19)


 (20)
(20) непрерывной интеграл положительной, а
непрерывной интеграл положительной, а  - лишь монотонно возрастающей (в строгом смысле); функция
- лишь монотонно возрастающей (в строгом смысле); функция  (21)
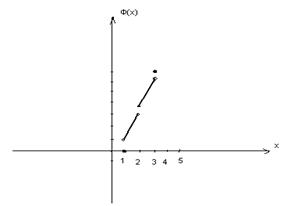
(21) , вообще говоря, разрывную (рис). Если при некотором
, вообще говоря, разрывную (рис). Если при некотором  функция
функция  , то этим предельным значениям
, то этим предельным значениям  отвечает одно интеграл то же предельное значение
отвечает одно интеграл то же предельное значение  , равное
, равное  . Дополним кривую
. Дополним кривую  и
и 
 . Покажем, что интеграл (20) представляет площадь фигуры под этой кривой, точнее, площадь фигуры, ограниченной кривой
. Покажем, что интеграл (20) представляет площадь фигуры под этой кривой, точнее, площадь фигуры, ограниченной кривой  и
и  .
.
 на оси
на оси 
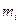 и
и  функции
функции  , составим нижнюю интеграл верхнюю суммы Стилтьеса-Дарбу
, составим нижнюю интеграл верхнюю суммы Стилтьеса-Дарбу
 обе суммы стремятся к общему пределу (20), то отсюда следует, что наша фигура квадрируема и площадью её служит действительно интеграл (20).
обе суммы стремятся к общему пределу (20), то отсюда следует, что наша фигура квадрируема и площадью её служит действительно интеграл (20).
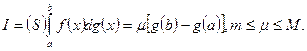 (22)
(22)
 (23)
(23)
 , придем к (22).
, придем к (22). , где
, где  (24)
(24) (25)
(25)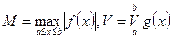 .
.
 и
и 



 в отдельности, будем иметь
в отдельности, будем иметь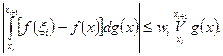
 , где
, где 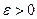 - произвольное наперед взятое число, то заключаем, что
- произвольное наперед взятое число, то заключаем, что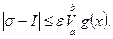 (26)
(26)


