
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава I. Развитие понятия интегралаСтр 1 из 8Следующая ⇒
Интеграл Лебега-Стилтьеса Содержание Введение Глава I. Развитие понятия интеграла 1.1 Проблема моментов Глава II. Интеграл Стилтьеса 2.1 Определение интеграла Стилтьеса 2.2 Общие условия существования интеграла Стилтьеса 2.3 Классы случаев существования интеграла Стилтьеса 2.4 Свойства интеграла Стилтьеса 2.5 Интегрирование по частям 2.6 Приведение интеграла Стилтьеса к интегралу Римана 2.7 Вычисление интегралов Стилтьеса 2.8 Примеры 2.10 Теорема о среднем, оценки 2.11 Предельный переход под знаком интеграла Стилтьеса 2.12. Примеры и дополнения Глава III. Применение интеграла Стилтьеса 3.1 Применение в теории вероятностей 3.2 Применение в квантовой механике Заключение Список литературы Приложение
Введение Понятие интеграла Римана, известное из элементарного курса анализа, применимо лишь к таким функциям, которые или непрерывны или имеют "не слишком много" точек разрыва. Для измеримых функций, которые могут быть разрывны всюду, где они определены (или же вообще могут быть заданы на абстрактном множестве, так что для них понятие непрерывности просто не имеет смысла), римановская конструкция интеграла становится непригодной. Вместе с тем для таких функций имеются аналоги в теории измерений: это интегралы Лебега и Стилтьеса. Так как интеграл Стилтьеса охватывает более широкий класс функций, мы остановимся на рассмотрении этого интеграла. Выбор темы обусловлен тем, что изучению интеграла Стилтьеса уделяется меньше внимания, чем интегралам Римана и Лебега, хотя именно идея стилтьесовского интегрирования богаче и плодотворней предыдущих, определение интеграла Стилтьеса шире классического и в некотором отношении удобнее его. Цель работы - рассмотреть необходимость введения понятия интеграла Стилтьеса, дать точное, компактное, сравнительно полное изложение теории интеграла Стилтьеса. Задачи, которые нужно выполнить для достижения цели: изучить множество литературы по этой теме; отобрать из изученного материла необходимый; привести примеры использования интеграла. Работа состоит из трёх глав. Первая посвящена развитию данного понятия, проблеме моментов, которая и привела к необходимости введения нового понятия интеграла.
Во второй главе рассмотрены основные понятия, определение самого интеграла, свойства, способы вычисления, рассмотрено множество примеров. Третья глава посвящена применению интеграла Стилтьеса в других разделах математики и в других науках.
Глава I. Развитие понятия интеграла Проблема моментов Введение понятия интеграла Стилтьеса и последующая его разработка связаны с проблемой моментов, состоящей в следующем. Пусть задана последовательность чисел Проблема моментов первоначально ставилась в менее общей форме. А именно по заданной последовательности чисел Ранние исследования Стилтьеса изложены в его статье о механических квадратурах, в которой выясняется, позволяют ли формулы квадратур получать неограниченное приближение интеграла в смысле Римана. Во вводной части статьи Стилтьес решает задачу об определении многочлена
Условиями
при неотрицательной Мы коснемся двух моментов из содержания его статьи. Первый относится к задаче о степени приближения, даваемого квадратурной формулой Гаусса:
Здесь Стилтьес пользуется доказанными им формулами П.Л. Чебышева в виде
где Он показывает, что если в квадратурной формуле Гаусса в качестве
так как в этом случае
Вторым моментом является следующий. Отметив, что его результаты полезны при изучении вопроса о квадратуре интеграла
Он ограничивается тем частным случаем, когда
является непрерывной и строго монотонной, а потому существует обратная функция
сводящих интеграл (4) к уже изученному Стилтьесом случаю. По поводу же общего случая Стилтьес указал, что "условия, налагаемые на функции Приведенные слова Стилтьеса показывают, что уже в 1884 г. он был в некоторой степени подготовлен к пересмотру понятия интеграла. К мысли о таком пересмотре его приводил прием замены переменных, который играл заметную роль в последующей истории интеграла Стилтьеса. Стилтьес рассматривал непрерывные дроби вида
где Пусть
причем, если ряд
если же ряд
и функции К этому времени математикам, занимавшимся непрерывными дробями, была известна связь между интегралом
и непрерывной дробью
где
Формулами
Этой-то связью и руководствовался Стилтьес в своих исследованиях. Ход его мысли был следующим. Для подходящих дробей дроби (6) справедливы следующие свойства: корни
или, в другой форме,
В частности, Как уже говорилось Пусть дробь вида (6) задана разложением в ряд по убывающим степеням
Тогда оказывается, что ряды
сходятся и
Эти формулы позволяют по цепной дроби (6) найти её разложение в ряд (9). Обратная же задача - по разложению (9) найти дробь (6) - неизбежно приводит к решению более или менее общей проблемы моментов. В самом деле, Стилтьесу была известна чебышевско-марковская интерпретация
Сумма
может быть названа моментом порядка
имеет значение Равным образом система масс Мы назовем проблемой моментов следующую задачу: Найти распределение положительной массы на прямой Действительно, формулы (10) приводят к постановке проблемы моментов, если принято истолкование Цепные дроби рассматривающегося П.Л. Чебышевым и А.А. Марковым типа получились из разложения интеграла (7) и все корни знаменателей их подходящих дробей были заключены в промежутке Физическое определение момента материальной точки в соединении с обычным для физиков и математиков переходом от момента точки к моменту отрезка приводило к новому определению интеграла, тесно связанному с функциями распределения.
Таким образом, именно для того, чтобы описать в форме некоторого аналитического выражения физическое понятие момента, Стилтьес ввел новое понятие интеграла, причем последнее, как это обычно и случается в математике, оказалось имеющим более общий характер, чем исходное физическое понятие. Он рассмотрел интеграл
Интегрирование по частям Для интегралов Стилтьеса имеет место формула
в предположении, что существует один из этих интегралов; существование другого отсюда уже вытекает. Формула эта носит название формулы интегрирования по частям. Докажем её. Пусть существует интеграл
Сумму Стилтьеса для интеграла
можно представить в виде
Если прибавить и опять отнять справа выражение
то
Выражение в фигурных скобках представляет собою стилтьесову сумму для интеграла
если в качестве выбранных из промежутков Как следствие нашего рассуждения, особо отметим тот любопытный факт, что если функция Это замечание позволяет добавить ряд новых случаев существования интеграла Стилтьеса к тем, которые были рассмотрены в п.3, переменив роли функций Примеры Вычислить по формуле (11) интегралы: а) б) в) Решение: а) б)
в) Вычислить по формуле (15) интегралы: а) б) Решение: а) Функция
б) Скачок 1 при Имеем:
Вычислить по формуле (15) интегралы: а) где
Решение: Функция
Поэтому а) Аналогично, б) в) Предположим, что вдоль отрезка
Разобьем промежуток
На отрезке
При стремлении к 0 всех
Можно было бы здесь сначала установить "элементарный" статический момент Аналогично для момента инерции
Важно подчеркнуть, что интеграл Стилтьеса дал возможность объединить одной интегральной формулой разнородные случаи непрерывно распределенных интеграл сосредоточенных масс! Пусть непрерывно распределенные массы имеют линейную плотность
В каждой же точке Если теперь разложить интеграл (16) по формуле (15), то получим
Всмотревшись в правую часть, легко в первом члене узнать статический момент непрерывно распределенных масс, а во втором - статический момент сосредоточенных масс. Аналогичный результат получится интеграл для интеграла (17). а) Составить выражение Решение:
В промежутке
б) То же самое - для такого распределения: массы величины 2 при Решение:
В промежутке
в) выяснить распределение масс, если Решение: Массы величины 1 в точках
6. Рассмотрим другой вопрос, в котором интеграл Стилтьеса играет такую же роль, как интеграл в упражнении 4). Предположим, что на балку (рис) покоящуюся на двух опорах, кроме непрерывно распределенной нагрузки действуют и сосредоточенные силы. Расположим ось Поставим задачей определить так называемый изгибающий момент Так как на элементе
то, "суммируя" получим
Аналогично, исходя из левой части балки, можно было бы получить (учитывая изменение положительного направления для отсчета моментов)
Легко непосредственно усмотреть, что оба выражения изгибающего момента в действительности тождественны. Их равенство равносильно условию
которое является следствием из условий равновесия
выражающих равенство нулю суммы всех сил интеграл суммы моментов (относительно начала) всех сил, действующих на балку. Если интенсивность непрерывно распределенной нагрузки обозначить через
Пусть сосредоточенные силы
В двух слагаемых правой части легко узнать моменты, порожденные порознь непрерывной нагрузкой интеграл сосредоточенными силами: интеграл Стилтьеса охватывает их единой интегральной формулой. Установим ещё один факт, интересный для теории сопротивления материалов. Произведя в формуле (18) интегрирование по частям, получим
Отсюда ясно, что всюду, за исключением точек приложения сосредоточенных сил, имеет место равенство
Пусть балка длины Решение: Формула (15) может оказаться полезной интеграл для вычисления обычных интегралов (в смысле Римана). Проиллюстрируем это на следующем примере. Пусть
так, что в каждой из частей функция Пусть, далее,
Тогда имеет место следующая формула:
Действительно, последовательно находим
двойная подстановка исчезает, а интеграл
width="288" height="51" border="0" /> Аналогично
и т.д. Установим в заключение, с помощью формулы (11) одно полезное обобщение формулы интегрирования по частям для обыкновенных интегралов. Именно, если
то справедлива формула
Для доказательства, по формуле (11) заменим интеграл слева интегралом Стилтьеса интеграл проинтегрируем по частям (п.5):
Остается ещё раз применить формулу (11) к последнему интегралу, чтобы прийти к (19). Здесь функции
Геометрическая иллюстрация интеграла Стилтьеса
Рассмотрим интеграл
предполагая функцию Система параметрических уравнений
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 640; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.67.16 (0.182 с.) |
 ; требуется найти такую функцию распределения
; требуется найти такую функцию распределения  , чтобы члены заданной последовательности были моментами, т.е.
, чтобы члены заданной последовательности были моментами, т.е. 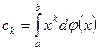 . Если a и b конечны, то поставленная задача называется проблемой моментов в конечном интервале; если
. Если a и b конечны, то поставленная задача называется проблемой моментов в конечном интервале; если  , то получаем проблему моментов Стилтьеса.
, то получаем проблему моментов Стилтьеса.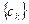 ищется такая функция
ищется такая функция  , чтобы имели место равенства
, чтобы имели место равенства  . Целесообразность привлечения интеграла Стилтьеса для постановки и решения проблемы моментов напрашивается довольно естественно. С таким положением вещей и столкнулся Стилтьес при изучении непрерывных дробей, и именно в результате этих исследований он предложил своё обобщение интеграла.
. Целесообразность привлечения интеграла Стилтьеса для постановки и решения проблемы моментов напрашивается довольно естественно. С таким положением вещей и столкнулся Стилтьес при изучении непрерывных дробей, и именно в результате этих исследований он предложил своё обобщение интеграла.

 (1)
(1) .
.



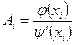 . (2)
. (2) брать числа
брать числа  , получаемые по формуле (2) из цепной дроби, соответствующей интегралу
, получаемые по формуле (2) из цепной дроби, соответствующей интегралу  , а
, а  будут корнями знаменателей подходящих дробей, то формула Гаусса даст сколь угодно точное приближение при возрастании
будут корнями знаменателей подходящих дробей, то формула Гаусса даст сколь угодно точное приближение при возрастании 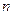 . Для этой цепной дроби числа
. Для этой цепной дроби числа 
 (3)
(3) .
. , Стилтьес ставит вопрос о квадратурных формулах для интеграла вида
, Стилтьес ставит вопрос о квадратурных формулах для интеграла вида . (4)
. (4) - произвольная интегрируемая по Риману функция, а
- произвольная интегрируемая по Риману функция, а  , в котором
, в котором  , и показывает, что в этом случае аппроксимация возможна со сколь угодно большой степенью точности. Доказательство этого факта опирается на то, что функция
, и показывает, что в этом случае аппроксимация возможна со сколь угодно большой степенью точности. Доказательство этого факта опирается на то, что функция (5)
(5) , и в интеграле (4) возможна замена переменных
, и в интеграле (4) возможна замена переменных
 , делаются источником трудностей, которых удастся избежать лишь с помощью новых исследований о самих принципах интегрального исчисления". Действительно, если
, делаются источником трудностей, которых удастся избежать лишь с помощью новых исследований о самих принципах интегрального исчисления". Действительно, если  .
. (6)
(6) - в общем случае комплексное число.
- в общем случае комплексное число. - подходящая дробь порядка
- подходящая дробь порядка 

 расходится, то
расходится, то

 и
и  различны.
различны. (7)
(7) , (8)
, (8) - суть линейные функции
- суть линейные функции  связаны с коэффициентами разложения (7) в ряд по убывающим степеням
связаны с коэффициентами разложения (7) в ряд по убывающим степеням 

 и
и  действительны и различны, степень
действительны и различны, степень 

 при
при  , а потому, если обозначить через
, а потому, если обозначить через  нули
нули  , то
, то  и
и  при
при  - нули функции
- нули функции  , то
, то  и
и  для случая нечетных
для случая нечетных  .
. (9)
(9)
 (10)
(10) , как массы, сосредоточенной в точке
, как массы, сосредоточенной в точке  , являющейся корнем
, являющейся корнем  . Естественно было распространить эту интерпретацию и на предельный случай, рассматривая
. Естественно было распространить эту интерпретацию и на предельный случай, рассматривая  как массы, расположенные в нулях функции
как массы, расположенные в нулях функции  распределение массы (положительной), при котором на расстоянии
распределение массы (положительной), при котором на расстоянии  от начала сосредоточена масса
от начала сосредоточена масса 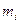 .
.
 масс относительно начала. В таком случае из предшествующих формул следует, что момент порядка
масс относительно начала. В таком случае из предшествующих формул следует, что момент порядка 

 .
. , где
, где 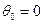 , будем иметь те же моменты
, будем иметь те же моменты  .
. , если даны моменты порядка
, если даны моменты порядка  ".
". как масс, а
как масс, а 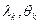 как соответствующих расстояний этих масс от начала координат.
как соответствующих расстояний этих масс от начала координат.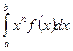 становилось недостаточным, существенно ограничивая класс последовательностей чисел
становилось недостаточным, существенно ограничивая класс последовательностей чисел  . Зная же эти функции, мы тем самым знаем решение системы уравнений (10), т.е. решение проблемы моментов. Если при этом
. Зная же эти функции, мы тем самым знаем решение системы уравнений (10), т.е. решение проблемы моментов. Если при этом  и
и  ,
,  и
и  попарно совпадут, то получится определенное решение: если же они попарно различны, то решений по крайней мере два: системы
попарно совпадут, то получится определенное решение: если же они попарно различны, то решений по крайней мере два: системы  и
и  . Следовательно, общность цепных дробей вида (6) достаточно широка, чтобы сделать вывод о разрешимости проблемы моментов для интервала
. Следовательно, общность цепных дробей вида (6) достаточно широка, чтобы сделать вывод о разрешимости проблемы моментов для интервала  для случая произвольной непрерывной
для случая произвольной непрерывной  (9)
(9) . Разложив промежуток
. Разложив промежуток  на части
на части 
 , выберем в этих частях произвольно по точке
, выберем в этих частях произвольно по точке 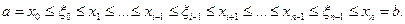




 перепишется так:
перепишется так:


 точек взять
точек взять  и
и  , соответственно,
, соответственно,  и
и  . Если, как обычно, положить
. Если, как обычно, положить  , то теперь длины всех частичных промежутков не превзойдут
, то теперь длины всех частичных промежутков не превзойдут 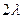 . При
. При  сумма в квадратных скобках стремится к
сумма в квадратных скобках стремится к  в промежутке
в промежутке  и
и  .
.
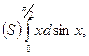




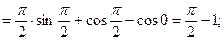

 где
где 
 где
где 
 и скачок - 2 при
и скачок - 2 при  ; в остальных точках
; в остальных точках  . Поэтому
. Поэтому
 и - 2 при
и - 2 при  (значение функции
(значение функции 
 б)
б)  в)
в) 

 . Производная
. Производная



 расположены массы, как сосредоточенные в отдельных точках, так интеграл распределенные непрерывно. Не делая различия между ними, обозначим для
расположены массы, как сосредоточенные в отдельных точках, так интеграл распределенные непрерывно. Не делая различия между ними, обозначим для 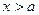 через
через  сумму всех масс, расположенных в промежутке
сумму всех масс, расположенных в промежутке  ; сверх того, положим,
; сверх того, положим,  . Очевидно,
. Очевидно, 
 содержится, очевидно, масса
содержится, очевидно, масса  . Точно так же на отрезке
. Точно так же на отрезке  содержится масса
содержится масса  . Считая массу во всех случаях сосредоточенной, например, на правом конце промежутка, получим для искомого статического момента приближенной выражение
. Считая массу во всех случаях сосредоточенной, например, на правом конце промежутка, получим для искомого статического момента приближенной выражение .
. , в пределе придем к точному результату:
, в пределе придем к точному результату: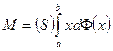 . (16)
. (16) , отвечающий отрезку оси от
, отвечающий отрезку оси от  , а затем "просуммировать" эти элементы.
, а затем "просуммировать" эти элементы. тех же масс относительно начал найдем формулу
тех же масс относительно начал найдем формулу (17)
(17) ; кроме них пусть в точках
; кроме них пусть в точках  расположены сосредоточенные массы
расположены сосредоточенные массы  . Тогда, исключая эти точки, функция
. Тогда, исключая эти точки, функция 
 функция испытывает скачок, равный именно массе
функция испытывает скачок, равный именно массе  , в этой точке сосредоточенной.
, в этой точке сосредоточенной.
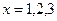 и непрерывно распределенные массы с плотностью 2 в промежутке
и непрерывно распределенные массы с плотностью 2 в промежутке  .
.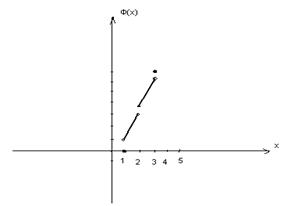
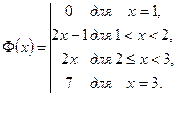
 в промежутке
в промежутке  .
.

 непрерывно распределенные массы с плотностью 1, в промежутке
непрерывно распределенные массы с плотностью 1, в промежутке  - массы с плотностью
- массы с плотностью 
 вертикально вниз (см. рис) Не делая различий между действующими силами, обозначим для
вертикально вниз (см. рис) Не делая различий между действующими силами, обозначим для 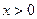 через
через 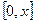 балки, включая интеграл реакции опор; далее, пусть
балки, включая интеграл реакции опор; далее, пусть  . Силу
. Силу  в произвольном сечении
в произвольном сечении  балки. Под этим разумеют сумму моментов всех сил, действующих на правую (или на левую) часть балки, относительно этого сечения. При этом, когда речь идет о правой части балки, момент считают положительным, если он вращает эту часть по часовой стрелке (для левой части - обратное правило).
балки. Под этим разумеют сумму моментов всех сил, действующих на правую (или на левую) часть балки, относительно этого сечения. При этом, когда речь идет о правой части балки, момент считают положительным, если он вращает эту часть по часовой стрелке (для левой части - обратное правило). , скажем, правой части балки приложена сила
, скажем, правой части балки приложена сила  , создающая элементарный момент
, создающая элементарный момент

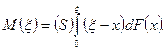


 , то, исключая точки, где приложены сосредоточенные силы, будет
, то, исключая точки, где приложены сосредоточенные силы, будет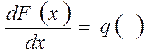
 приложены в точках
приложены в точках  . Тогда, очевидно, перерезывающее усилие именно в этих точках имеет скачки, соответственные равные
. Тогда, очевидно, перерезывающее усилие именно в этих точках имеет скачки, соответственные равные 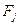 . Далее, применяя, например, к интегралу (18) формулу (15), получим
. Далее, применяя, например, к интегралу (18) формулу (15), получим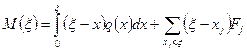 .
.


 несет "треугольную" нагрузку с интенсивностью
несет "треугольную" нагрузку с интенсивностью  ; кроме того, пусть к ней приложены сосредоточенная сила, равная 3, в точке
; кроме того, пусть к ней приложены сосредоточенная сила, равная 3, в точке  , интеграл реакции опор, обе равные - 3 (они устанавливаются по закону рычага). Определить перерезывающее усилие
, интеграл реакции опор, обе равные - 3 (они устанавливаются по закону рычага). Определить перерезывающее усилие  .
.
 величину скачка
величину скачка 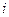 -й производной
-й производной  в
в  -й точке
-й точке  .
. и, вообще,
и, вообще, 

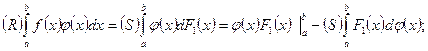
 <="" div="">
<="" div="">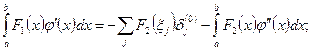
 и
и 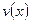 обе абсолютно интегрируемы в промежутке
обе абсолютно интегрируемы в промежутке  и
и  определяются интегральными формулами:
определяются интегральными формулами:

 (19)
(19)


 (20)
(20) непрерывной интеграл положительной, а
непрерывной интеграл положительной, а  - лишь монотонно возрастающей (в строгом смысле); функция
- лишь монотонно возрастающей (в строгом смысле); функция  (21)
(21)


