
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приведение интеграла Стилтьеса к интегралу Римана
Пусть функция
На рисунке изображен график функции Именно, если ограничиться лишь теми значениями
связанного со скачком функции Докажем теперь, что
где последний интеграл берется в обычном смысле, его существование обеспечено, так как функция С этой целью разложим промежуток
и составим стилтьесову сумму
Если положить
Так как
Это выражение имеет вид римановой суммы для интеграла
Отсюда, однако, нельзя ещё непосредственно заключить, переходя к оператору, о равенстве (10), ибо даже при Имеем
и
так что
Предположим теперь при то одновременно и
В таком случае
Этим доказано, что
откуда и следует (10).
Несмотря на принципиальную важность полученного результата, он не дает практически удобного средства для вычисления интеграла Стилтьеса. Как осуществлять вычисление в некоторых простейших случаях, мы покажем в следующем пункте.
|
|||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 270; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.238.76 (0.007 с.) |
 непрерывна в промежутке
непрерывна в промежутке  , а
, а  монотонно возрастает в этом промежутке, и притом в строгом смысле. Тогда, как показал Лебег, интеграл Стилтьеса
монотонно возрастает в этом промежутке, и притом в строгом смысле. Тогда, как показал Лебег, интеграл Стилтьеса  с помощью подстановки
с помощью подстановки  непосредственно приводится к интегралу Римана.
непосредственно приводится к интегралу Римана.
 , при которых функция
, при которых функция  и
и  . Так создается непрерывная линия, которая каждому значению
. Так создается непрерывная линия, которая каждому значению  между
между  и
и  относит одно определенное значение
относит одно определенное значение  между
между  и
и  . Эта функция
. Эта функция  , очевидно, будет непрерывной и монотонно возрастающей в широком смысле; её можно рассматривать как своего рода обратную для функции
, очевидно, будет непрерывной и монотонно возрастающей в широком смысле; её можно рассматривать как своего рода обратную для функции 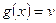 . Но из промежутка значений
. Но из промежутка значений 
 имеет себе соответствующее значение
имеет себе соответствующее значение  рядом вертикальных отрезков.
рядом вертикальных отрезков. (10)
(10)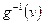 , а с нею и сложная функция
, а с нею и сложная функция 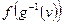 , непрерывна.
, непрерывна.
 .
. , то будем иметь
, то будем иметь
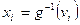 , то
, то .
.
 может оказаться, что
может оказаться, что  к нулю не стремится, если, например, между безгранично сближающимися
к нулю не стремится, если, например, между безгранично сближающимися  и
и  будет заключено значение
будет заключено значение 

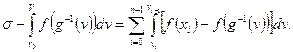
 настолько малыми, чтобы колебания функции
настолько малыми, чтобы колебания функции  были меньше произвольного наперед заданного числа
были меньше произвольного наперед заданного числа 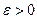 . Так как
. Так как , очевидно,
, очевидно, 

 .
.



