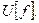Применение в квантовой механике

Аппарат стилтьесовского интегрирования приспособлен для единообразного описания дискретных и непрерывных явлений. Это обстоятельство оказалось решающим и при введении его в математический арсенал квантовой механики.

Если в механике раньше пользовались в основном классическим математическим анализом - аппаратом, приспособленным для описания определенного класса непрерывных явлений, а в тех случаях, когда нужно было описать дискретные явления, прибегали к теории рядов, конечных или бесконечных, то в квантовой механике такие приемы оказались недостаточными. Непрерывные и дискретные аспекты переплелись в ней настолько тесно, что идея их единообразного описания напрашивалась сама собой.

Идея стилтьесовского интегрирования могла оказаться полезной с самого начала. Но в момент зарождения квантовой механики и некоторое время спустя интегрирование по Стилтьесу было еще недостаточно разработано, а главное - слишком мало известно, чтобы лечь в основу квантовой механики. И Дирак повернул направление ее развития в ином направлении.

Дирак в качестве исходной позиции тож ставит проблему единообразного описания дискретных и непрерывных явлений. При этом за основное понятие он берет понятие непрерывности, а дискретное описывает в терминах последнего. Против такого подхода сразу восстал И. Нейман, предложив заменить обобщенные функции интегралами Стилтьеса. Большинство физиков не приняло концепции Неймана, тем не менее он продолжал отстаивать и развивать свою точку зрения, подробно изложив свои соображения в своей монографии. И хотя его концепция была принята не сразу, тем не менее в квантовой механике интеграл Стилтьеса нашел своё применение.

Интеграл Стилтьеса и линейные функционалы.

Понятие функционала явилось предметом многочисленных исследований, восходящих ещё к Эйлеру. Среди этих исследований важное место заняли изыскания по аналитическому изображению функционалов.

В явной форме понятие функционала сформулировал Вольтера в 1887году. Он же дал и первое аналитическое выражение для некоторого класса функционалов в виде выражения, аналогичного ряду Тейлора с привлечением понятия производной функционала. В теории функций наиболее распространенным способом изображения функций является выражение их рядами того или иного типа. По аналогии начались попытки представления функционалов в виде рядов по функционалам

,

где - некоторые константы, зависящие от природы разлагаемого в ряд функционала , а - определенная последовательность фиксированных функционалов. Первым таким разложением было разложение, предложенное Пинкерле и Амальди в 1901 г. Оно имело вид:

,

где с - некоторое фиксированное число промежутка , на котором задано рассматриваемое множество функций .

Кроме них предложили общие выражения линейных функционалов Фреше и Адамар, но все эти способы пригодны только для относительно узких классов непрерывных функций. Поэтому поиски новых аналитических выражений для функционалов продолжались.

Решающим в этом направлении был результат Рисса. В 1909 г. Он доказал, что всякий линейный функционал , определенный в пространстве непрерывных функций , заданных на , раастояние между которыми выражается интегралом Стилтьеса

где - функция с ограниченным изменением, определяемая через

 

Заключение

Интеграл, который мы рассмотрели в данной работе, был введен Стилтьесом. Новое понятие ему было нужно, как мы уже говорили в первой главе, в разрабатывавшейся им теории цепных дробей; он ввел его и применил в интересовавших его вопросах. Разработка же выпала на доли других математиков, таких, как Кёниг, А.А. Марков, А.М. Ляпунов, Г.Ф. Вороной, Рисс, Гильберт, Хеллингер, причем каждый из них пришел к понятию интеграла Стилтьеса, отправляясь от разных задач. В теории цепных дробей применяли его сам Стилтьес и А.А. Марков, в теории R-интеграла - Кёниг, в теории чисел - Г.Ф. Вороной, в небесной механике - А.М. Ляпунов, в теории интегральных уравнений - Гильберт, Хеллингер, в теории линейных функционалов - Рисс. В дальнейшем разработкой интеграла занимались также У.Г. Юнг и Радон. Юнг использовал интеграл Стилтьеса в теории тригонометрических рядов, Радон применял также в теории линейных функционалов, в теории интегральных уравнений.

Очень велико число работ, посвященных изучению различных свойств интеграла Стилтьеса. Это работы Хелли, Брэй, Гильдебрандт, Р. Юнг, Г.М. Шварц, Яджи и др.

Совершенно необозримо поле приложений различных типов интеграла Стилтьеса. Разумеется, та исходная проблема, из которой родилось само понятие интеграла Стилтьеса, - проблема моментов, - не перестала быть связанной с этим понятием. После работ Стилтьеса, Маркова, Юнга и других ученых, о которых сказано выше, поток применений интеграла Стилтьеса вырос в трудно обозримый комплекс. Многие разделы математики невозможно представить без использования интеграла Стилтьеса.

Идея стилтьесовского интегрирования использовалась и продолжает использоваться при изучении различных вопросов математики, физики, квантовой механики. Поэтому данная работа может быть использована в качестве пособия для студентов физико-математичсеких факультетов.

 

Список литературы

1. Александров П.С., Колмогоров А. Введение в теорию функций действительного переменного. Изд.3-е, переработ. М. - Л., Гостехтеориздат., 1938г.

2. Брудно А.Л. Теория функций действительного переменного. Избранные главы.М., "Наука", 1971

3. Гливенко В.И. Интеграл Стилтьеса. - М., 1936, 216с.

4. Гохман Э.Х. Интеграл Стилтьеса и его приложения. Государственное издательство физ. - мат. литературы, М., 1958

5. Дьяченко М.И., Ульянов П.Л. Мера и интеграл. - М.: Издательство "Факториал Пресс", 2002. - 160с.

6. Камке Э. Интеграл Лебега-Стилтьеса. Перевод с немецкого Г.П. Сафроновой. Под ред. И.П. Натансона. - М.: Государственное издательство физ. - мат. литературы, 1959г.

7. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа: Учебник для вузов. - 6-е изд., испр. - М.: Наука, Главная редакция физ. - мат. Литературы, 1989. - 624 с.

8. Леонтьева Т.А. и др. Задачи по теории функций действительного переменного: Учеб. Пособие по спец. "Математика"/ Панферов В.С., Серов В.С. - М.: Изд-во МГУ, 1997 - 208с.

9. Макаров И.П. Теория функций действительной переменной. Под ред. И.Я. Верченко - М.: Государственное издательство "Высшая школа" - 1965

10. Медведев Ф.А. Развитие понятия интеграла. - М., "Наука", 1974г.

11. Песин И.Н. Развитие понятия интеграла, М., "Наука", 1966. - 207с.

12. Самородницкий А.А. Теория меры/ Сыктывкар. Гос. Университет. - Л.: Издательство ЛГУ, 1990. - 267с.

13. Теория функций вещественной переменной. И.П. Натансон. Главная редакция физико-математической литературы издательства "Наука", 1974

14. Теория функций и функциональный анализ: [Сборник статей/ Науч. ред. проф. Б.М. Гагаев]. - Казань: Издательство Казанского университета, 1976г. - 98с.

15. Тимофеев А.Ф. Интегрирование функций. М. - Л. Издательство технико-теоретической литературы, 1948

16. Толстов Г.П. Мера и интеграл. Главная редакция физ. - мат. Литературы, "Наука", 1976г

17. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. В трех томах. Том III/ - СПб.: Издательство Лань, 1997. - 672с.

18. Фролов Н.А. Теория функций действительного переменного. Учебное пособие для пединститутов. Изд-во 2-е, М., Учпедгиз, 1961

19. Эйлер Л. Интегральное исчисление. Т.2. Пер. с латинского. - М., Гостехтеориздат., 1957. - 368с.

20. go. mail

21. www.aggregateria

 

Приложение

СТИЛТЬЕС ТОМАС ИОАННЕС (Stieltjes Thomas Johannes 1856-1894).

Стилтьес Томас Иоаннес (29.12.1856-31.12.1894) - нидерландский математик и астроном. Член Нидерландской Академии наук (1886г) Родился в Зволле. Окончил Политехническую школу в Делфте. В 1877-1883гг. работал в Лейденской обсерватории, с 1886г. - профессор Тулузского университета. Научные исследования Стилтьеса в основном касаются теории функциональных непрерывных дробей, проблемы моментов, теории ортогональных многочленов, приближенного интегрирования и других вопросов классического анализа. Обобщенное Стилтьесом понятие интеграла Римана играет важную роль в современной математике. Известно также интегральное преобразование Стилтьеса.