
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Взаимное расположение двух прямых.Содержание книги
Поиск на нашем сайте
Если прямые заданы своими общими уравнениями
условием совпадения этих прямых является:
условием параллельности этих прямых является:
условием перпендикулярности этих прямых является:
Если известны угловые коэффициенты прямых
а условие перпендикулярности:
т.е. угловые коэффициенты этих прямых обратны по абсолютной величине и противоположны по знаку. Угол между двумя прямыми. Возьмем две прямые
Пусть Рис. 5 Из геометрических соображений устанавливаем зависимость между углами
или
Расстояние от точки до прямой. Чтобы найти расстояние от данной точки до данной прямой, надо уравнение прямой привести к общему виду, вместо текущих координат подставить в левую часть уравнения координаты данной точки и взять абсолютную величину полученного результата. То есть: если уравнение прямой
точка
Пример №1. В треугольнике Решение: Сделаем схематический чертеж треугольника (рис. 6).
Рис.6 Сначала определим координаты точки Длину медианы определим по формуле расстояния между двумя точками
Далее составим уравнение стороны
Пример №2. Даны прямые Решение:
Таким образом, угол
Пример №3. Через точку пересечения прямых Решение: 1. Находим точку
2. Найдем угловой коэффициент прямой, перпендикулярной к прямой 3. Запишем уравнение искомой прямой: 4. Найдем расстояние полученной прямой от начала координат:
Пример №4. Перевозка груза от данного города в первый пункт, находящийся на расстоянии 100 км, стоит 200 грн., а в другой, находящейся на расстоянии 400 км – стоит 350 грн. Найти стоимость перевозки на единицу расстояния и расходы, не связанные с расстоянием. Определить также стоимость перевозки груза на расстояние 875 км. Решение. Подставляя данные в уравнение
Тогда стоимость перевозки
В частности, стоимость перевозки на расстояние 875 км:
|
||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 385; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |


 и
и  , то условием пересечения этих прямых является:
, то условием пересечения этих прямых является: ,
, ,
, ,
, .
. и
и  , то условие параллельности этих прямых состоит в равенстве их угловых коэффициентов:
, то условие параллельности этих прямых состоит в равенстве их угловых коэффициентов: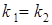 ,
, ,
, и
и  ; уравнение
; уравнение  , где
, где  , а уравнение
, а уравнение  , где
, где  (рис. 5).
(рис. 5).
 – угол между прямыми
– угол между прямыми  .
.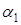 и
и  ,
, 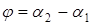 . Отсюда:
. Отсюда: ,
, . (3.11)
. (3.11) ,
, имеет координаты
имеет координаты  , то расстояние от прямой
, то расстояние от прямой  до точки
до точки  . (3.12)
. (3.12) , заданном координатами своих вершин:
, заданном координатами своих вершин:  ,
,  и
и  . Найти: а) длину медианы
. Найти: а) длину медианы  , проведенной из вершины
, проведенной из вершины  ; б) длину высоты
; б) длину высоты  , опущенной из вершины
, опущенной из вершины  .
.
 , как точки, делящей отрезок
, как точки, делящей отрезок 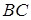 пополам:
пополам:  ,
,  ; т.е.
; т.е.  .
. .
.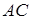 , используя уравнение прямой, проходящей через две точки (3.9)
, используя уравнение прямой, проходящей через две точки (3.9)  , а длину
, а длину  ;
;  ;
;  ;
; .
. . Найти угол между ними.
. Найти угол между ними.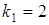 ,
,  . Тогда по формуле (3.11) находим:
. Тогда по формуле (3.11) находим: .
. .
. и
и  проведена прямая перпендикулярно первой из данных прямых. Найти расстояние полученной прямой от начала координат.
проведена прямая перпендикулярно первой из данных прямых. Найти расстояние полученной прямой от начала координат.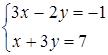
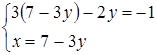



 . Следовательно
. Следовательно  .
. ,
,  , т.к.
, т.к.  , то искомый угловой коэффициент
, то искомый угловой коэффициент 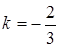 .
. или
или 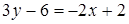 ;
;  .
. .
. , получим систему уравнений:
, получим систему уравнений:
 грн.,
грн.,  грн. – ее решения.
грн. – ее решения. на расстояние
на расстояние  выражается уравнением:
выражается уравнением: .
. (грн.)
(грн.)


