
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение прямой в отрезках на осях.
Задача. Составить уравнение прямой, отсекающей на оси абсцисс отрезок величины Решение.
Пусть данная прямая отсекает на оси абсцисс отрезок
Рис. 7
Составим уравнение данной прямой, как прямой, проходящей через две точки
Уравнение (3.13) называется уравнением прямой в отрезках на осях. В этом уравнении Замечание. Это уравнение удобно использовать для геометрического построения прямой откладывая на оси абсцисс отрезок, равный по величине Важнейшие кривые второго порядка
Эллипс. Эллипсом ( рис8 ) называется множество точек, сумма расстояний которых от двух фиксированных точек, называемых фокусами эллипса, есть величина постоянная
Рис. 8 Каноническое уравнение эллипса, изображенного на рисунке 8, имеет вид:
где Вершинами эллипса называются точки Окружность – частный случай эллипса, при условии, что полуоси эллипса
Общее уравнение окружности имеет вид:
Для определения координат центра и радиуса окружности, заданной общим уравнением, нужно с помощью тождественных преобразований уравнения (3.16) привести к виду (3.15) Гипербола.
Гиперболой (рис.9) называется множество точек, абсолютная величина разности расстояний которых от двух фиксированных точек, называемых фокусами, есть величина постоянная Рис. 9 (а)
Рис. 9 (б)
Каноническое уравнение гиперболы, изображенной на рисунке 9(а) имеет вид:
где Гипербола имеет две оси симметрии (координатные оси), с одной из которых (осью абсцисс), она пересекается в двух точках Отрезок Эксцентриситетом гиперболы называется отношение расстояния между фокусами к ее действительной оси, т.е. Гипербола имеет две асимптоты, уравнения которых: Если мнимая ось гиперболы направлена по оси
Эксцентриситет этой гиперболы Если оси координат совпадают с асимптотами равносторонней гиперболы рис. (9в), то ее уравнение в этой системе координат имеет вид:
Рис. 9 (в)
Переменные величины 3. Парабола. Парабола
Рис. 10 (а)
Рис. 10 (б)
Параболой называется множество точек, равноудаленных от данной точки, называемой фокусом, и прямой, называемой директрисой параболы. Каноническое уравнение параболы, изображенной на рисунке 10: а) б) Величина Пример №1. Составить уравнение эллипса, зная, что он проходит через точки Решение. Возьмем каноническое уравнение эллипса
определим параметры эллипса Обозначив
решая ее, плучим, что
Следовательно, искомое уравнение эллипса будет:
Пример №2. Дано уравнение гиперболы Решение. Приведем уравнение гиперболы к каноническому виду и определим как параметры гиперболы, так и расстояние
Откуда:
Эксцентриситет Действительная ось: Мнимая ось: Уравнения директрис: Уравнения асимптот: Пример №3. Две реки Решение. Найдем уравнение касательной к кривой
Так как точка касания единственная, то
Уравнение касательной имеет вид:
Рис. 11 Канал должен быть направлен по нормали
Из системы Находим Точка
ІV. Введение в анализ
Пусть каждому
или кратко:
Или кратко:
Обозначение: На геометрическом языке определение предела означает, что вне любой
Если последовательность имеет предел, то говорят что она сходится, в противном случае она расходится. Если
Свойства. 1. Алгебраическая сумма двух и более бесконечно малых величин есть величина бесконечно малая. 2. Произведение бесконечно малой на ограниченную функцию есть величина бесконечно малая.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 452; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.244.201 (0.046 с.) |
 , а на оси ординат – отрезок величины
, а на оси ординат – отрезок величины  .
.
 , а на оси ординат отрезок
, а на оси ординат отрезок  . Тогда координаты точки
. Тогда координаты точки  будут
будут  , а координаты точки
, а координаты точки  будут
будут  (рис. 7).
(рис. 7). и
и 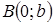 . Подставляя координаты точек
. Подставляя координаты точек  или
или  .
.
 . (3.13)
. (3.13) и
и  – текущие координаты,
– текущие координаты,  и
и  – параметры.
– параметры. , большая, чем расстояние между фокусами
, большая, чем расстояние между фокусами  .
.
 , (3.14)
, (3.14) .
. и
и  ,
,  и
и  пересечения эллипса с его осями симметрии (осями координат) отрезки
пересечения эллипса с его осями симметрии (осями координат) отрезки  и
и  , длины которых соответственно равны
, длины которых соответственно равны  и
и  , называются большой и малой осями соответственно. Параметры
, называются большой и малой осями соответственно. Параметры  . Очевидно, что
. Очевидно, что  .
. равны между собой
равны между собой  . Каноническое уравнение окружности с центром в точке
. Каноническое уравнение окружности с центром в точке  и радиусом
и радиусом  имеет вид:
имеет вид: . (3.15)
. (3.15)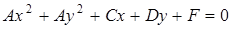 . (3.16)
. (3.16)


 . (3.17)
. (3.17) .
. – длиной
– длиной  .
. .
. и имеет длину
и имеет длину  , в соответствии с рисунком 9(б), то уравнение гиперболы имеет вид:
, в соответствии с рисунком 9(б), то уравнение гиперболы имеет вид: .
.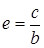 . Ее асимптоты те же, что и у гиперболы на рисунке 9(а). Гиперболы, изображенные на рисунке 9, называются сопряженными. Если
. Ее асимптоты те же, что и у гиперболы на рисунке 9(а). Гиперболы, изображенные на рисунке 9, называются сопряженными. Если  . (3.18)
. (3.18)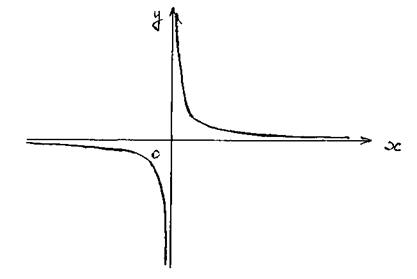
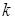 – постоянное число, называются обратно пропорциональными.
– постоянное число, называются обратно пропорциональными. или
или  .
.

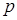 , равная расстоянию от фокуса до директрисы, называется параметром параболы; прямая, проходящая через фокус параболы перпендикулярно ее директрисе, называется ее осью, а точка пересечения параболы с ее осью – вершиной параболы.
, равная расстоянию от фокуса до директрисы, называется параметром параболы; прямая, проходящая через фокус параболы перпендикулярно ее директрисе, называется ее осью, а точка пересечения параболы с ее осью – вершиной параболы. и
и  .
. , а затем координаты точки
, а затем координаты точки  . Из получившейся системы уравнений:
. Из получившейся системы уравнений:
 ;
;  сведем данную систему к следующей системе:
сведем данную систему к следующей системе: ,
, ,
,  откуда
откуда 
 .
. .
. . Найти длины ее осей, координаты фокусов, эксцентриситет, составить уравнение директрис и асимптот гиперболы.
. Найти длины ее осей, координаты фокусов, эксцентриситет, составить уравнение директрис и асимптот гиперболы. от начала координат до фокуса:
от начала координат до фокуса: или
или  .
. .
. .
. .
. .
. .
. .
. .
. , река
, река  . Соединяющий реки канал должен иметь наименьшую длину. Как его нужно проложить?
. Соединяющий реки канал должен иметь наименьшую длину. Как его нужно проложить?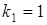 . Тогда
. Тогда  ;
; 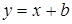 – уравнение касательной. Определим
– уравнение касательной. Определим  .
.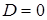 .
. .
. . Следовательно, координаты точки касания удовлетворяют системе уравнений:
. Следовательно, координаты точки касания удовлетворяют системе уравнений: .
. – точка касания, ближайшая к реке
– точка касания, ближайшая к реке 

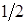

 , уравнение которой:
, уравнение которой: или
или  .
. .
. .
. – конец канала.
– конец канала. поставлено в соответствие некоторое действительное число:
поставлено в соответствие некоторое действительное число:  , то есть рассматривается функция натурального аргумента. В этом случае говорят, что задана последовательность вещественных чисел, которую записывают в строчку в порядке возрастания номеров:
, то есть рассматривается функция натурального аргумента. В этом случае говорят, что задана последовательность вещественных чисел, которую записывают в строчку в порядке возрастания номеров:

 существует число
существует число 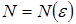 такое, что при всех
такое, что при всех  выполняется неравенство:
выполняется неравенство:
 .
.
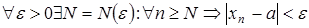 .
. .
. – окрестности точки
– окрестности точки  . Это число, разумеется, зависит от
. Это число, разумеется, зависит от 









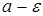

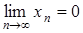 , то величина
, то величина  .
.


