
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие предела функции, свойства.
Пусть функция
Или кратко:
На геометрическом языке это определение означает, что Под проколотой
Обозначение: § § Практическое вычисление пределов основано на следующих теоремах: 1. Функция 2. Арифметические действия над пределами: Если § § § 3. Первый замечательный предел:
4. Второй замечательный предел:
Раскрытие некоторых видов неопределенностей. Вычисление предела в каждом конкретном случае требует индивидуального подхода. Решение одних примеров сводится непосредственно к применению теорем о свойствах бесконечно малых, а в других необходимо избавиться от неопределенностей вида:
Рассмотрим решение нескольких примеров. Пример №1. Вычислить: Решение. Числитель и знаменатель дроби при
т.е. Пример №2.
Решение. Неопределенность типа
Пример №3. Вычислить: Решение. Используем замену переменной. Пусть Пример перепишем в виде:
Пример №4. Вычислить: Решение. Вычислим, используя первый замечательный предел. Пусть
Пример №5. Вычислить: Решение. Используя тригонометрическое преобразование имеем:
Пример №6. Вычислить: Решение. Неопределенность
(т.к. Замечание. Проведенные преобразования фактически сводятся к делению числителя и знаменателя дроби на старшую степень Пример №7. Вычислить: Решение. Используя тригонометрические преобразования, имеем:
Пример №8. Вычислить: Решение. Для решения используем второй замечательный предел
Пример №9. Вычислить: Решение.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 268; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.0.240 (0.02 с.) |
 задана на интервале
задана на интервале  , исключая возможно точку
, исключая возможно точку 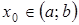 .
. называется пределом функции
называется пределом функции  , если для любого
, если для любого  существует
существует 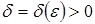 такое, что при всех
такое, что при всех  , удовлетворяющих условию
, удовлетворяющих условию  выполнено:
выполнено:  .
.
 .
.














 – окрестности точки
– окрестности точки  - окрестность точки
- окрестность точки  – окрестности точки
– окрестности точки  лежит в
лежит в 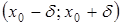 , исключая саму точку
, исключая саму точку 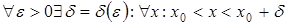
 выполнено:
выполнено:
 (для левостороннего предела);
(для левостороннего предела); (для правостороннего предела).
(для правостороннего предела).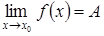 и
и  , то справедливы утверждения:
, то справедливы утверждения: ;
;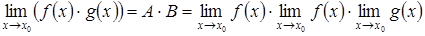 ;
; , при условии, что
, при условии, что  .
. . (4.1)
. (4.1) или
или  . (4.2)
. (4.2) и др.
и др. .
. стремится к нулю (принято говорить, что получается неопределенность вида
стремится к нулю (принято говорить, что получается неопределенность вида  ). Эту неопределенность создает множитель
). Эту неопределенность создает множитель  , называемый критическим. Необходимо от него избавиться путем алгебраических преобразований, т.е.:
, называемый критическим. Необходимо от него избавиться путем алгебраических преобразований, т.е.: ;
; .
. .
.
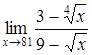 .
. , тогда
, тогда  и если
и если  , то
, то  , т.е.
, т.е.  .
. ;
;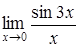 .
.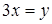 , тогда
, тогда 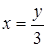 . Если
. Если  , то
, то 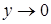 . Используя эту замену имеем:
. Используя эту замену имеем: .
. .
. .
. (неопределенность
(неопределенность  ).
). величина числителя определяется главным образом членом
величина числителя определяется главным образом членом  , а роль остальных слагаемых тем незначительней, чем больше
, а роль остальных слагаемых тем незначительней, чем больше 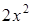 . Поэтому присутствие членов, содержащих
. Поэтому присутствие членов, содержащих  , является причиной возникновения неопределенности
, является причиной возникновения неопределенности 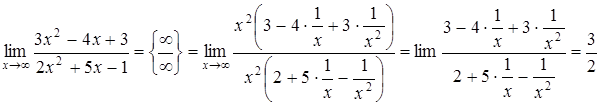 ,
, есть бесконечно малые при
есть бесконечно малые при  ).
). , при
, при 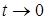 .
. (неопределенность
(неопределенность  ).
). .
. (неопределенность
(неопределенность  ).
). . Имеем:
. Имеем: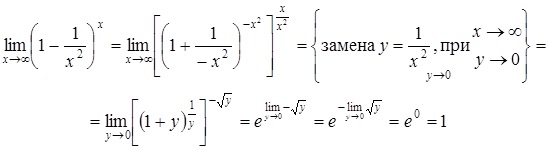
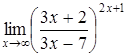 (неопределенность
(неопределенность 



