
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Технічний редактор О.І. ШелудькоСтр 1 из 9Следующая ⇒
Технічний редактор О.І. Шелудько
Зведений план – 2003 р., позиція №306 Підписано до друку “15” 05 2003 р. Формат 60/841/16 Папір друкарськ. Умовн. др.арк. – Тираж 164 прим. Друк – різографія. Замовлення № ________________________________________________________________ Донецький державний університет економіки і торгівлі Ім. М. Туган-Барановського ВРЦ, ДонДУЕТ, м. Донецьк –50, вул. Щорса, 31, тел. 337-93-61
введение
В практической деятельности человека математика используется с момента своего зарождения. Долгое время развитие математики определялось в основном потребностями естественных и технических наук. И лишь последнее время математическое моделирование процессов и явлений постепенно проникло во все новые сферы научных знаний: физику, химию, биологию и, наконец, общественные науки, в частности, экономику, социологию, политологию. Построение рыночных отношений в экономике требует резкого повышения качества подготовки специалистов – выпускников высших учебных заведений. Учитывая специфику учебного процесса студентов ускоренной формы обучения заочного отделения возникает необходимость в методической разработке по основным темам курса высшей математики, которая предназначена для теоретического и практического изучения. Знания, полученные при изучении курса математики, являются базовыми, на которые опираются такие математические курсы, как теория вероятностей, математические методы исследования операций, а также ряда экономико-математических дисциплин, а также для изучения специальных дисциплин, таких как теоретическая и прикладная механика, сопротивление материалов и т.п. В настоящей методической разработке рассматриваются следующие вопросы: § элементы линейной и векторной алгебры; § аналитической геометрии на плоскости; § пределы; § дифференциальное и интегральное исчисление; § дифференциальные уравнения. Основная цель этого пособия – оказать помощь студентам-заочникам ускоренной формы обучения по специальности «Технология питания» в выполнении контрольной работы. Выбор варианта осуществляется следующим образом: берем две последние цифры номера зачетной книжки, если число меньше или равно 35 то это Ваш вариант; если это число больше 35, то отнимаем от него число кратное 35 и получаем Ваш вариант.
Например: две последние цифры номера зачетной книжки 98, то Работа, выполненная не по своему варианту, не зачитывается. Правила оформление контрольной работы: 1. Контрольную работу необходимо выполнять в отдельной тетради, оставляя справа поля для замечаний рецензента. 2. В заголовке работы должны быть указаны фамилия и инициалы студента, факультет, курс, группа, учебный номер (шифр). Заголовок работы надо поместить на обложке тетради. 3. Необходимо записывать полное условие каждой задачи перед ее решением. 4. Решение задач записывать подробно, сопровождая необходимыми пояснениями. 5. В конце выполненной контрольной работы необходимо перечислить использованную при решении литературу. Защита контрольной работы проводится в форме собеседования по теме работы. I. Элементы линейной алгебры
Матрицы и определители Операции над матрицами.
1) Умножение матрицы на число. Произведением матрицы Например: если Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы. 2) Сложение матриц. Суммой двух матриц
3) Вычитание матриц. Разность двух матриц одинакового размера определяется через предыдущие операции:
4) Умножение матриц. Умножение матрицы Пример. Вычислить произведение матриц
Решение. 1. Найдем размер матрицы-произведения (если умножение матриц возможно):
2. а) свойства сложения матриц:
б) свойства умножения матриц:
Однако имеются и специфические свойства матриц.
5) Возведение в степень. Целой положительной степенью
Замечание: эта операция определяется только для квадратичных матриц. 6) Транспонирование матриц. Переход от матрицы Например: Свойства операции транспонирования: 1) 2) 3) 4)
Обратная матрица
Мы показали, что все основные действия над числами можно производить и над матрицами. Возникает вопрос, можно ли найти матрицу Понятие обратной матрицы вводится только для квадратной матрицы.
Чтобы найти обратную матрицу 1. Вычислить определитель матрицы 2. Найти алгебраические дополнения 3. Записать обратную матрицу по формуле:
обратив внимание на то, что матрица, составленная из алгебраических дополнений, транспонированна. Чтобы сделать проверку, необходимо перемножить данную и обратную матрицы. В результате должна получиться единичная матрица. Пример:
Решение.
Проверка:
Основные понятия Вектором называется направленный отрезок Длиной (или модулем) вектора Если начало и конец вектора совпадают, например Ортом или единичным вектором называется вектор, длина которого равна, единице. Равными называются два вектора, если они расположены на параллельных прямых и имеют одинаковые длину и направление. Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными. Компланарными называются три вектора, если они параллельны некоторой плоскости. Суммой нескольких векторов называется вектор, по величине и направлению равный замыкающей пространственной ломанной линии, построенной на данных векторах. Произведением вектора Проекцией вектора Координатами вектора
Координаты вектора Длина (модуль) вектора При сложении (вычитании) векторов их координаты складываются (вычитаются), при умножении вектора на число его координаты умножаются на это число.
Пример №1. Даны векторы а) векторы б) длины векторов в) скалярный квадрат вектора г) скалярное произведение векторов д) угол между векторами Решение. а) По определению б) По формуле
в) По формуле
г) По формуле
д) По формуле
откуда Пример №2. Найти синус угла между векторами: Решение. Из формулы
Находим
откуда Пример №3. Найти проекцию вектора Решение. По формуле (2.3) имеем:
Пример №4. Проверить, будут ли три данных вектора Решение: Для этого достаточно проверить, выполняется ли условие компланарности векторов:
Проверим:
Значит, векторы
На плоскости Аналитическая геометрия есть область математики, изучающая геометрические образы алгебраическими методами. Еще в VII веке французским математиком Рене Декартом был разработан и впервые применен так называемый «метод координат», позволяющий переводить геометрические понятия на алгебраический язык. В основе «метода координат» лежит понятие системы координат. Прямоугольная система координат на плоскости устанавливает взаимнооднозначное соответствие между множеством всех точек плоскости и множеством пар чисел (рис. 1), которое дает возможность при решении геометрических задач применять алгебраические методы.
Доказательство. Точки
обозначим через
Рис. 3 Отрезки, заключенные между параллельными прямыми
но Отсюда:
Из этих уравнений найдем неизвестные Полагая в формулах (3.2)
т.е. координаты середины отрезка равны полусуммам, одноименных координат его концов.
Линии первого порядка
Пусть на плоскости заданы: прямоугольная система координат и некоторая линия
связывающее переменные величины
Поскольку величины Понятие уравнения линии дает возможность сводить геометрические задачи к алгебраическим. Пример. Составить уравнение прямой, проходящей через точки Решение: Подставляя данные координаты в соотношение (3.9.), получаем:
Задача. Издержки производства 100 ед. некоторого товара составляют 300 тыс. грн., а 500 ед. – 600 тыс. грн. Определить издержки производства 400 ед. товара при условии, что функция издержек линейна. Решение. Используя уравнение прямой, проходящей через две точки
Подставляя
Общее уравнение прямой
определяет прямую линию. Доказательство. Первое утверждение теоремы мы уже доказали в п.3. Если прямая не перпендикулярна Докажем обратное утверждение. Пусть дано уравнение (3.10). Если Если Линии, определяемые уравнением первой степени, называются линиями первого порядка. Уравнение вида Пересечение двух прямых. Пусть две прямые заданы общими уравнениями
Решение даст точку пересечения этих прямых. Если система не имеет решения, то прямые не пересекаются, т.е. не имеют общей точки. Угол между двумя прямыми. Возьмем две прямые
Пусть Рис. 5 Из геометрических соображений устанавливаем зависимость между углами
или
Пример №1. В треугольнике
Решение: Сделаем схематический чертеж треугольника (рис. 6).
Рис.6 Сначала определим координаты точки Длину медианы определим по формуле расстояния между двумя точками
Далее составим уравнение стороны
Пример №2. Даны прямые Решение:
Таким образом, угол
Пример №3. Через точку пересечения прямых Решение: 1. Находим точку
2. Найдем угловой коэффициент прямой, перпендикулярной к прямой 3. Запишем уравнение искомой прямой: 4. Найдем расстояние полученной прямой от начала координат:
Пример №4. Перевозка груза от данного города в первый пункт, находящийся на расстоянии 100 км, стоит 200 грн., а в другой, находящейся на расстоянии 400 км – стоит 350 грн. Найти стоимость перевозки на единицу расстояния и расходы, не связанные с расстоянием. Определить также стоимость перевозки груза на расстояние 875 км. Решение. Подставляя данные в уравнение
Тогда стоимость перевозки
В частности, стоимость перевозки на расстояние 875 км:
Задача. Составить уравнение прямой, отсекающей на оси абсцисс отрезок величины Решение.
Пусть данная прямая отсекает на оси абсцисс отрезок
Рис. 7
Составим уравнение данной прямой, как прямой, проходящей через две точки
Уравнение (3.13) называется уравнением прямой в отрезках на осях. В этом уравнении Замечание. Это уравнение удобно использовать для геометрического построения прямой откладывая на оси абсцисс отрезок, равный по величине Эллипс. Эллипсом ( рис8 ) называется множество точек, сумма расстояний которых от двух фиксированных точек, называемых фокусами эллипса, есть величина постоянная
Рис. 8 Каноническое уравнение эллипса, изображенного на рисунке 8, имеет вид:
где Вершинами эллипса называются точки Окружность – частный случай эллипса, при условии, что полуоси эллипса
Общее уравнение окружности имеет вид:
Для определения координат центра и радиуса окружности, заданной общим уравнением, нужно с помощью тождественных преобразований уравнения (3.16) привести к виду (3.15) Гипербола.
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 236; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.108.241 (0.217 с.) |
 , значит Ваш вариант: №28.
, значит Ваш вариант: №28. на число
на число  называется матрица
называется матрица  , элементы которой
, элементы которой  .
. , то
, то 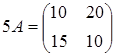
 одинакового размера
одинакового размера  называется матрица
называется матрица  , элементы которой
, элементы которой  .
. ,
,  ,
,  .
. .
. называется такая матрица
называется такая матрица 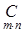 , каждый элемент которой
, каждый элемент которой  равен сумме произведений элементов
равен сумме произведений элементов  -ой строки матрицы
-ой строки матрицы 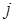 -го столбца матрицы
-го столбца матрицы 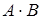 , где
, где ;
;  .
. .
.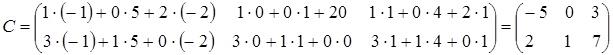 Многие свойства, присущие операциям над числами, справедливы и для операций над матрицами:
Многие свойства, присущие операциям над числами, справедливы и для операций над матрицами: ;
; ;
; .
.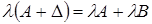 ;
; ;
; ;
; .
. , т.е. коммутативный (переместительный) закон умножения, вообще говоря, не выполняется.
, т.е. коммутативный (переместительный) закон умножения, вообще говоря, не выполняется.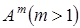 квадратной матрицы
квадратной матрицы  матриц, равных
матриц, равных  .
. , в которой строки и столбцы поменялись местами с сохранением порядка.
, в которой строки и столбцы поменялись местами с сохранением порядка.
 .
. ;
;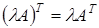 ;
;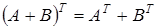 ;
; .
. , такую, что
, такую, что 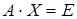 . Если она существует, то ее называют обратной матрицей.
. Если она существует, то ее называют обратной матрицей. и удовлетворяющая условиям
и удовлетворяющая условиям

 .
.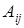 ко всем элементам матрицы
ко всем элементам матрицы  (1.4)
(1.4) . Найти
. Найти 









 ;
;
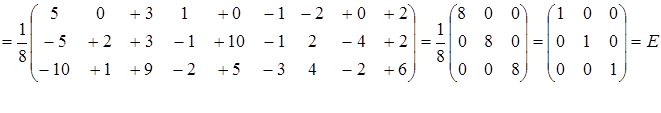
 ІІ. Элементы векторной алгебры
ІІ. Элементы векторной алгебры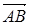 с начальной точкой
с начальной точкой  .
. , изображающего вектор. Обозначение
, изображающего вектор. Обозначение  .
.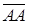 , то такой вектор называется нулевым и обозначается
, то такой вектор называется нулевым и обозначается  . Длина нулевого вектора равна нулю:
. Длина нулевого вектора равна нулю:  . Так как направление нулевого вектора произвольно, то считают, что он коллинеарен любому вектору.
. Так как направление нулевого вектора произвольно, то считают, что он коллинеарен любому вектору. на число
на число  , имеющий длину
, имеющий длину  , направление которого совпадает с направлением вектора
, направление которого совпадает с направлением вектора  , и противоположно ему, если
, и противоположно ему, если  .
. на ось
на ось  (обозначение
(обозначение  ) называется число, равное длине вектора
) называется число, равное длине вектора  , взятое со знаком плюс, если направление вектора совпадает с направлением оси
, взятое со знаком плюс, если направление вектора совпадает с направлением оси  и
и  соответственно проекции точек
соответственно проекции точек  , где
, где  -угол между вектором
-угол между вектором  и записываются:
и записываются:  или
или  .
. и
и  , то
, то  .
. .
. . Найти:
. Найти: и
и  ;
; и
и 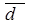 ;
; ;
; ;
; ,
,  ;
; ;
; .
. – скалярный квадрат равен квадрату модуля вектора, т.е.
– скалярный квадрат равен квадрату модуля вектора, т.е. .
.
 .
. угол между векторами
угол между векторами  ,
, .
. и
и  .
. получим, что
получим, что 

 .
.


 .
. на вектор
на вектор  .
.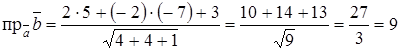 .
. ,
,  и
и  компланарны.
компланарны. .
.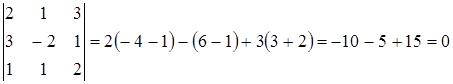
 - компланарны.
- компланарны.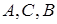 проектируем на оси координат, их проекции на ось
проектируем на оси координат, их проекции на ось 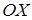

 , а на ось
, а на ось  через
через  (рис. 3).
(рис. 3). и
и  пропорциональны. Следовательно:
пропорциональны. Следовательно: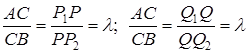 ,
, ,
, 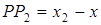 ,
,  ,
,  .
. ,
,  .
. и
и  , получим исходные формулы (3.2). Теорема доказана.
, получим исходные формулы (3.2). Теорема доказана. , имеем:
, имеем: ,
, 
 . Рассмотрим соотношение вида:
. Рассмотрим соотношение вида: , (3.3)
, (3.3) и
и  , их называют текущими координатами.
, их называют текущими координатами. и
и  .
. или
или  .
. и
и  , получаем:
, получаем: или
или  .
.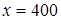 , вычисляем издержки производства 400 единиц товара:
, вычисляем издержки производства 400 единиц товара: (грн.)
(грн.) (3.10)
(3.10) (см. (3.6.)), т.е. уравнение вида (3.10), где
(см. (3.6.)), т.е. уравнение вида (3.10), где  . Если прямая перпендикулярна оси
. Если прямая перпендикулярна оси  , то все ее точки имеют одинаковые абсциссы, равные величине отрезка, отсекаемого прямой на оси
, то все ее точки имеют одинаковые абсциссы, равные величине отрезка, отсекаемого прямой на оси 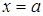 , что также является уравнением первой степени вида (3.10.), где
, что также является уравнением первой степени вида (3.10.), где 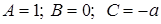 .
. , то (3.10) можно записать в виде
, то (3.10) можно записать в виде  . Полагая
. Полагая  , получим уравнение
, получим уравнение  и
и  , то (3.10) примет вид
, то (3.10) примет вид  . Обозначая –
. Обозначая –  через
через  , получим
, получим  и
и  . Найдем точку пресечения этих прямых. Очевидно, что она будет принадлежать как первой, так и второй прямой. Следовательно, ее координаты должны удовлетворять обоим уравнениям. Поэтому для отыскания точки пересечения нужно решить систему уравнений:
. Найдем точку пресечения этих прямых. Очевидно, что она будет принадлежать как первой, так и второй прямой. Следовательно, ее координаты должны удовлетворять обоим уравнениям. Поэтому для отыскания точки пересечения нужно решить систему уравнений:
 и
и  ; уравнение
; уравнение  , где
, где  , а уравнение
, а уравнение  , где
, где  (рис. 5).
(рис. 5).
 – угол между прямыми
– угол между прямыми  .
.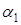 и
и  ,
, 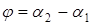 . Отсюда:
. Отсюда: ,
, . (3.11)
. (3.11) , заданном координатами своих вершин:
, заданном координатами своих вершин:  ,
,  и
и  . Найти: а) длину медианы
. Найти: а) длину медианы  , проведенной из вершины
, проведенной из вершины  , опущенной из вершины
, опущенной из вершины 
 , как точки, делящей отрезок
, как точки, делящей отрезок 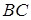 пополам:
пополам:  ,
,  ; т.е.
; т.е.  .
. .
.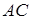 , используя уравнение прямой, проходящей через две точки (3.9)
, используя уравнение прямой, проходящей через две точки (3.9)  , а длину
, а длину  ;
;  ;
;  ;
; .
. . Найти угол между ними.
. Найти угол между ними.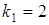 ,
,  . Тогда по формуле (3.11) находим:
. Тогда по формуле (3.11) находим: .
. .
. и
и  проведена прямая перпендикулярно первой из данных прямых. Найти расстояние полученной прямой от начала координат.
проведена прямая перпендикулярно первой из данных прямых. Найти расстояние полученной прямой от начала координат.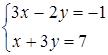
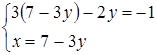



 . Следовательно
. Следовательно  .
. ,
,  , т.к.
, т.к.  , то искомый угловой коэффициент
, то искомый угловой коэффициент 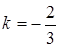 .
. или
или 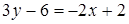 ;
;  .
. .
.
 грн.,
грн.,  грн. – ее решения.
грн. – ее решения. .
. (грн.)
(грн.) , а на оси ординат – отрезок величины
, а на оси ординат – отрезок величины  .
.
 , а на оси ординат отрезок
, а на оси ординат отрезок  . Тогда координаты точки
. Тогда координаты точки  , а координаты точки
, а координаты точки  (рис. 7).
(рис. 7). и
и 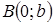 . Подставляя координаты точек
. Подставляя координаты точек  или
или  .
.
 . (3.13)
. (3.13) – параметры.
– параметры. , большая, чем расстояние между фокусами
, большая, чем расстояние между фокусами  .
.
 , (3.14)
, (3.14) .
. и
и  ,
,  и
и  пересечения эллипса с его осями симметрии (осями координат) отрезки
пересечения эллипса с его осями симметрии (осями координат) отрезки  и
и  , длины которых соответственно равны
, длины которых соответственно равны  и
и  , называются большой и малой осями соответственно. Параметры
, называются большой и малой осями соответственно. Параметры  . Очевидно, что
. Очевидно, что  .
. равны между собой
равны между собой  . Каноническое уравнение окружности с центром в точке
. Каноническое уравнение окружности с центром в точке  и радиусом
и радиусом  имеет вид:
имеет вид: . (3.15)
. (3.15)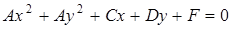 . (3.16)
. (3.16)


