
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определители квадратных матриц
Определитель матрицы
Определителем матрицы третьего порядка, или определителем третьего порядка, называется число, которое вычисляется одним из трех способов: І способ: Правило треугольников или правило Сарруса:
На этом рисунке указано правило вычисления членов, учитываемых со своим знаком, а также правило вычисления членов с обратным знаком. Определитель будет равен алгебраической сумме всех произведений, то есть:
ІI способ – это способ вычисления определителей третьего порядка, заключающийся в дописывании первых двух столбцов, в нахождении произведений по главной диагонали и параллелях к ней и по обычной диагонали и параллелях к ней. То есть:
ІІІ способ – с помощью разложения по строке или столбцу. Необходимо ввести следующие определения: 1. Минором 2. Алгебраическим дополнением
т.е. алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца Определитель равен сумме произведений элементов какой-либо строки (или столбца) определителя Например, для столбцов этот способ нахождения определителя
эта формула называется разложением определителя по элементам Пример:
Таким образом, применяя формулу (1.3), мы сводим вычисление определителя третьего порядка к вычислению определителей второго порядка. Обратная матрица
Мы показали, что все основные действия над числами можно производить и над матрицами. Возникает вопрос, можно ли найти матрицу Понятие обратной матрицы вводится только для квадратной матрицы.
Чтобы найти обратную матрицу 1. Вычислить определитель матрицы 2. Найти алгебраические дополнения 3. Записать обратную матрицу по формуле:
обратив внимание на то, что матрица, составленная из алгебраических дополнений, транспонированна. Чтобы сделать проверку, необходимо перемножить данную и обратную матрицы. В результате должна получиться единичная матрица. Пример:
Решение.
Проверка:
Основные понятия Вектором называется направленный отрезок Длиной (или модулем) вектора Если начало и конец вектора совпадают, например Ортом или единичным вектором называется вектор, длина которого равна, единице. Равными называются два вектора, если они расположены на параллельных прямых и имеют одинаковые длину и направление. Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными. Компланарными называются три вектора, если они параллельны некоторой плоскости. Суммой нескольких векторов называется вектор, по величине и направлению равный замыкающей пространственной ломанной линии, построенной на данных векторах. Произведением вектора Проекцией вектора
Координатами вектора Координаты вектора Длина (модуль) вектора При сложении (вычитании) векторов их координаты складываются (вычитаются), при умножении вектора на число его координаты умножаются на это число.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.13.255 (0.015 с.) |
 обозначается
обозначается  или
или  . Определителем матрицы второго порядка, или определителем второго порядка, называется число, которое вычисляется по формуле:
. Определителем матрицы второго порядка, или определителем второго порядка, называется число, которое вычисляется по формуле: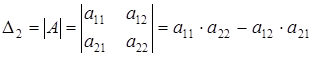 (1.1)
(1.1)






 (1.2)
(1.2)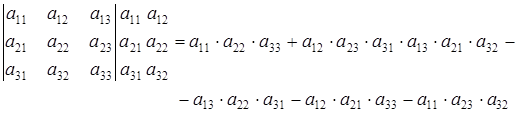
 элемента
элемента  матрицы
матрицы  -го порядка называется определитель матрицы
-го порядка называется определитель матрицы  -го порядка, полученной из матрицы
-го порядка, полученной из матрицы  -й строки и
-й строки и 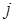 -го столбца.
-го столбца.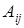 элемента
элемента  :
: ,
,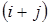 – четное число, и отличается от минора знаком, когда
– четное число, и отличается от минора знаком, когда  , (1.3)
, (1.3)


 , такую, что
, такую, что 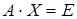 . Если она существует, то ее называют обратной матрицей.
. Если она существует, то ее называют обратной матрицей. и удовлетворяющая условиям
и удовлетворяющая условиям

 .
. (1.4)
(1.4) . Найти
. Найти 









 ;
;
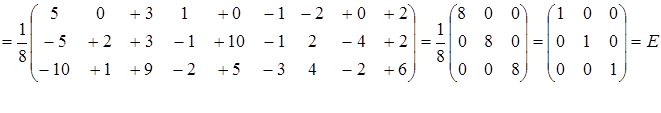
 ІІ. Элементы векторной алгебры
ІІ. Элементы векторной алгебры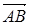 с начальной точкой
с начальной точкой  (который можно перемещать параллельно самому себе). Обозначение:
(который можно перемещать параллельно самому себе). Обозначение:  .
. , изображающего вектор. Обозначение
, изображающего вектор. Обозначение  .
.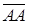 , то такой вектор называется нулевым и обозначается
, то такой вектор называется нулевым и обозначается  . Длина нулевого вектора равна нулю:
. Длина нулевого вектора равна нулю:  . Так как направление нулевого вектора произвольно, то считают, что он коллинеарен любому вектору.
. Так как направление нулевого вектора произвольно, то считают, что он коллинеарен любому вектору. на число
на число  называется вектор
называется вектор  , имеющий длину
, имеющий длину  , направление которого совпадает с направлением вектора
, направление которого совпадает с направлением вектора  , и противоположно ему, если
, и противоположно ему, если  .
. на ось
на ось  (обозначение
(обозначение  ) называется число, равное длине вектора
) называется число, равное длине вектора  , взятое со знаком плюс, если направление вектора совпадает с направлением оси
, взятое со знаком плюс, если направление вектора совпадает с направлением оси  и
и  соответственно проекции точек
соответственно проекции точек  , где
, где  -угол между вектором
-угол между вектором  и записываются:
и записываются:  или
или  .
. и
и  , то
, то  .
. .
.


