
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общая схема исследования функций и построения их графиков
1. Найти область определения функции. 2. Исследовать функцию на четность – нечетность, периодичность. 3. Найти точки пересечения графика функции с осями координат. 4. Исследовать функцию на непрерывность; найти точки разрыва (если они существуют) и установить характер разрыва. 5. Найти асимптоты кривой. 6. Найти интервалы возрастания и убывания функции и ее экстремумы. 7. Найти интервалы выпуклости и вогнутости кривой и точки ее перегиба. 8. На основе проверенного анализа построить график функции Пример. Исследовать функцию Решение. 1. Область определения 2. Функция четная, так как 3. Вертикальные асимптоты могут пересекать ось абсцисс в точках 4. Поведение функции в бесконечности. Вычислим 5. Экстремумы и интервалы монотонности. Найдем Однако критической точкой является только точка 1. Интервалы выпуклости и точки перегиба. Найдем:
Очевидно, что 7. Точки пересечения с осями
По данным исследований строим график:
VІ. Интегральное исчисление Понятие неопределеннного интеграла, свойства
В частности:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 261; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.156.212 (0.006 с.) |
 и построить ее график.
и построить ее график. , т.е.
, т.е.  .
. , и ее график симметричен относительно оси ординат.
, и ее график симметричен относительно оси ординат. . Так как пределы функции при
. Так как пределы функции при  (слева) и при
(слева) и при  (справа) бесконечны, т.е.
(справа) бесконечны, т.е. 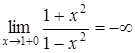 и
и 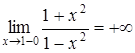 , то прямая
, то прямая  есть вертикальная асимптота. В силу симметрии графика
есть вертикальная асимптота. В силу симметрии графика  также вертикальная асимптота.
также вертикальная асимптота. . В силу четности имеем также
. В силу четности имеем также 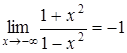 , т.е. прямая
, т.е. прямая  - горизонтальная асимптота.
- горизонтальная асимптота. ;
;  при
при  и
и  не существует при
не существует при  .
. (так как значения
(так как значения  , а при
, а при  , то
, то 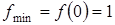 - минимум функции. На интервалах
- минимум функции. На интервалах  и
и  функция убывает, на интервалах
функция убывает, на интервалах  и
и  - возрастает.
- возрастает. .
. на интервале
на интервале  и функция выпукла вниз на этом интервале
и функция выпукла вниз на этом интервале  на интервалах
на интервалах  ,
,  и на этих интервалах функция выпукла вверх. Точек перегиба нет.
и на этих интервалах функция выпукла вверх. Точек перегиба нет. , т.е. точка пересечения с осью ординат
, т.е. точка пересечения с осью ординат  . Уравнение
. Уравнение  решений не имеет, следовательно, график функциии не пересекает ось абсцисс.
решений не имеет, следовательно, график функциии не пересекает ось абсцисс.



 называется первообразнойфункцией для функции
называется первообразнойфункцией для функции  на промежутке
на промежутке  , если в каждой точке
, если в каждой точке  .
.
 . Таким образом:
. Таким образом:
 ,где
,где
 .
.


