
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение прямой с угловым коэффициентом.
Пусть дана некоторая прямая, не перпендикулярная оси
Рис. 4
В таком случае Тангенс угла наклона к оси
Обозначим через
Отсюда, учитывая формулу (3.4), получим:
Так как точка
или
Уравнение (3.6.) называют уравнением прямой с угловым коэффициентом. Уравнение прямой, проходящей через данную точку с данным угловым коэффициентом. В ряде случаев встречается необходимость составить уравнение прямой, зная одну ее точку
Уравнение прямой, проходящей через две заданные точки. Пусть даны точки
Отсюда:
Подставив
Это уравнение, если
Замечание. При выводе уравнение (3.9) мы получим формулу (3.8) углового коэффициента прямой, проходящей через две данные точки Пример. Составить уравнение прямой, проходящей через точки Решение: Подставляя данные координаты в соотношение (3.9.), получаем:
Задача. Издержки производства 100 ед. некоторого товара составляют 300 тыс. грн., а 500 ед. – 600 тыс. грн. Определить издержки производства 400 ед. товара при условии, что функция издержек линейна. Решение. Используя уравнение прямой, проходящей через две точки
Подставляя
Общее уравнение прямой
определяет прямую линию. Доказательство. Первое утверждение теоремы мы уже доказали в п.3. Если прямая не перпендикулярна Докажем обратное утверждение. Пусть дано уравнение (3.10). Если Если Линии, определяемые уравнением первой степени, называются линиями первого порядка. Уравнение вида Пересечение двух прямых. Пусть две прямые заданы общими уравнениями
Решение даст точку пересечения этих прямых. Если система не имеет решения, то прямые не пересекаются, т.е. не имеют общей точки.
|
||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 449; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.28.48 (0.007 с.) |
 . Назовем углом наклона данной прямой к оси
. Назовем углом наклона данной прямой к оси  , на который нужно повернуть против часовой стрелки ось
, на который нужно повернуть против часовой стрелки ось 
 .
.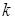 :
: . (3.4)
. (3.4) переменную точку с текущими коэффициентами
переменную точку с текущими коэффициентами  и
и  . Кроме того, введем в рассмотрение точку
. Кроме того, введем в рассмотрение точку  , в которой прямая пересекает ось
, в которой прямая пересекает ось  . Из треугольника
. Из треугольника  (рис. 4).
(рис. 4). .
.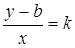 . (3.5)
. (3.5) лежит на данной прямой, то уравнение (3.5) является уравнением данной прямой, которое после преобразования примет вид:
лежит на данной прямой, то уравнение (3.5) является уравнением данной прямой, которое после преобразования примет вид:
 . (3.6.)
. (3.6.) и направление, в котором проходит эта прямая. Так как искомая прямая проходит через точку
и направление, в котором проходит эта прямая. Так как искомая прямая проходит через точку  . Определяя «
. Определяя « » из этого равенства и подставляя его в уравнение (3.6), получим искомое уравнение прямой:
» из этого равенства и подставляя его в уравнение (3.6), получим искомое уравнение прямой: . (3.7)
. (3.7) . Приняв в равенстве (3.7) точку
. Приняв в равенстве (3.7) точку  , получим:
, получим: .
. . (3.8)
. (3.8) .
. , можно записать в виде:
, можно записать в виде: . (3.9)
. (3.9) и
и  .
. или
или  .
. и
и  , получаем:
, получаем: или
или  .
.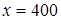 , вычисляем издержки производства 400 единиц товара:
, вычисляем издержки производства 400 единиц товара: (грн.)
(грн.) (3.10)
(3.10)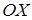 , то она определяется уравнением первой степени
, то она определяется уравнением первой степени  . Если прямая перпендикулярна оси
. Если прямая перпендикулярна оси 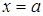 , что также является уравнением первой степени вида (3.10.), где
, что также является уравнением первой степени вида (3.10.), где 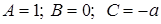 .
. , то (3.10) можно записать в виде
, то (3.10) можно записать в виде  . Полагая
. Полагая  , получим уравнение
, получим уравнение  и
и  , то (3.10) примет вид
, то (3.10) примет вид  . Обозначая –
. Обозначая –  через
через  , получим
, получим 
 и
и  . Найдем точку пресечения этих прямых. Очевидно, что она будет принадлежать как первой, так и второй прямой. Следовательно, ее координаты должны удовлетворять обоим уравнениям. Поэтому для отыскания точки пересечения нужно решить систему уравнений:
. Найдем точку пресечения этих прямых. Очевидно, что она будет принадлежать как первой, так и второй прямой. Следовательно, ее координаты должны удовлетворять обоим уравнениям. Поэтому для отыскания точки пересечения нужно решить систему уравнений:



