
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Простейшие способы интегрирования.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Непосредственное интегрирование. Способ непосредственного интегрирования основан на использовании свойств неопределенного интеграла и приведении подынтегрального выражения к табличной форме. Пример. òВычислить (2х3 – 3x2 + 2х –7)dx. Решение. В данном примере под знаком интеграла стоит алгебраическая сумма функций. Согласно свойству 5 неопределенного интеграла. ò (2х3 – 3х2 +2х –7)dx = ò 2x3dx - ò 3x2dx + ò 2xdx - ò 7dx. Последовательно применяя свойство 4 интегралов и формулы 1 и 2, получаем ò (2х3 – 3х2 + 2х – 7)dx = 2 ò x3dx -3 ò x2dx + 2 ò xdx - 7 ò dx= = Интегрирование подстановкой (заменой переменной). Этот способ заключается в переходе от данной переменной интегрирования к другой переменной для упрощения подынтегрального выражения и приведения его к одному из табличных. òВ интеграле f(x)dx сделаем подстановку x = j(t), где j(t) – функция, имеющая непрерывную производную. Тогда: f(x) = f(j(t)); dx = ¢j(t)dt; ò f(x)dx = ò f(j(t))¢j(t)dt. Пример. òВычислить sin7x cos xdx. Решение. Вычислим интеграл, использовав метод подстановки: Интегрирование по частям. Если и = и(х) и
или
Это и есть формула интегрирования по частям.
35. Основные методы интегрирования.
1. Первообразная, понятие неопределенного интеграла.. При введении понятия производной данной функции нами была рассмотрена задача о нахождении мгновенной скорости точки по известному закону ее движения S= S(t). В механике встречается обратная задача: по известному закону изменения скорости V= V(t) найти закон движения, то есть найти такую функцию S= S(t) производная которой равна V(t). Эта задача приводит к понятию первообразной функции. Определение: функция F(x) называется первообразной для функции f(x) на интервале (a, b), если функции f(x) и F(x) определены на этом интервале, функция F(x) дифференцируема на интервале (a, b) и в каждой точке интервала выполняется равенство
Первообразная существует для любой функции, непрерывной на отрезке. II. Свойства неопределенного интеграла. Перечислим основные свойства неопределенного интеграла, вытекающие из определения (3) и равенства (4): свойство 1: т.к. свойство 2: т.к.
свойство 3: Свойства (1) и (3) показывают, что знаки дифференциала и интеграла, стоящие рядом, взаимно уничтожаются. свойство 4: (свойство линейности неопределенного интеграла):
36. Таблица неопределенных интегралов от простейших функций.
Таблица простейших неопределённых интегралов 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Формулы (2.7) – (2.16) простейших неопределённых интегралов следует выучить наизусть. Знание их необходимо, но далеко не достаточно для того, чтобы научиться интегрировать. Устойчивые навыки в интегрировании достигаются только решением достаточно большого числа задач (обычно порядка 150 – 200 примеров различных типов).
37. Рациональные дроби. Основные понятия. Разложение рациональной дроби на простейшие.
Торема Правильную рациональную дробь
где Без доказательства. Согласно данному разложению, линейным множителям знаменателя Пример. Разложить на элементарные дроби Решение. Выделим из неправильной дроби целую часть, деля числитель на знаменатель
Разложим полученную в результате дробь на элементарные слагаемые:
Тогда Для нахождения коэффициентов разложения, чаще всего используется метод неопределенных коэффициентов и метод частных значений. Метод неопределенных коэффициентов.Суть метода неопределенных коэффициентов состоит в следующем. ▪ Раскладываем правильную рациональную дробь ▪ Простейшие дроби приводим к общему знаменателю ▪ Многочлен, получившийся в числителе, приравниваем к многочлену
▪ Для тождественного равенства двух многочленов необходимо и достаточно, чтобы коэффициенты при одинаковых степенях
38. Интегрирование простейших рациональных дробей.
Определение: Элементарными называются дроби следующих четырех типов: I. II. m, n – натуральные числа (m ³ 2, n ³ 2) и b2 – 4ac <0. Первые два типа интегралов от элементарных дробей довольно просто приводятся к табличным подстановкой t = ax + b. I. II. Рассмотрим метод интегрирования элементарных дробей вида III. Интеграл дроби вида III может быть представлен в виде:
Здесь в общем виде показано приведение интеграла дроби вида III к двум табличным интегралам
39. Интегрирование тригонометрических выражений.
Рациональные функции. Условимся через Интегралы вида Будем рассматривать интегралы вида Заметим, что в интегральном исчислении нет общих правил. Интегрирование может быть выполнено не единственным способом. Но даже и тогда, когда имеется теоретическое правило вычисления интеграла, оно может оказаться далеко не лучшим. Для вычисления интегралов вида Действительно, пусть
Подставляя в подынтегральное выражение вместо
Подынтегральная функция рациональна относительно
40. Интегрирование некоторых иррациональных функций.
Класс иррациональных функций очень широк, поэтому универсального способа их интегрирования просто быть не может. В этой статье попытаемся выделить наиболее характерные виды иррациональных подынтегральных функций и поставить им в соответствие метод интегрирования.
· Используя метод непосредственного интегрирования, достаточно просто находятся неопределенные интегралы вида Пример. Найти множество первообразных функции Решение. Правило интегрирования Ответ:
41. Определенный интеграл. Определение, геометрический смысл.
Сопоставляя доказанную теорему с решением задачи III, видим, что криволинейная трапеция, рассмотренная в упомянутой задаче, имеет площадь F, причем эта площадь выражается формулой
Читая эту формулу справа налево, находим Геометрический смысл определенного интеграла. Если f (x) непрерывна и положительна на [ a, b ], то интеграл
представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f (x) (см. рис. 5.).
Не следует думать, что условие непрерывности функции необходимо для того, чтобы у нее существовал определенный интеграл. Интеграл может существовать и у разрывной функции. Пусть, например, функция f (x), заданная на промежутке [ a, b ], равна нулю во всех точках этого промежутка, кроме конечного числа точек z 1, z 2,..., zN. Составим для f (x) интегральную сумму σ. Пусть из точек ξ 0, ξ 1,..., ξn -1, входящих в определение σ, p точек совпадают с точками zi, а остальные отличны от них. Тогда в сумме σ будет лишь p слагаемых, отличных от нуля. Если наибольшее из чисел | f (zi) | (i = 1, 2,..., N) есть K, то, очевидно, | σ | ≤ Kpλ ≤ KNλ, откуда ясно, что при λ → 0 будет и σ → 0. Таким образом, интеграл
существует и равен нулю. Приведем теперь пример функции, не имеющей интеграла. Пусть φ (x) задана на промежутке [0, 1] так:
Если мы, составляя сумму σ, за точки ξk выберем числа иррациональные, то окажется σ = 0. Если же все ξk взять рациональными, то получится σ = 1. Таким образом, за счет одного лишь уменьшения λ нельзя приблизить σ к какому-либо постоянному числу, и интеграл
не существует. В настоящее время известны точные признаки, позволяющие судить, имеет или нет заданная функция определенный интеграл, но мы ограничимся вышеприведенной теоремой об интегрируемости непрерывных функций.
42. Основные свойства определенного интеграла.
1. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е. II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.
III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.
IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.
V. Постоянный множитель можно выносить за знак определенного интеграла.
VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.
43. Вычисление определенного интеграла. Формула Ньютона-Лейбница.
Формула Ньютона-Лейбница. Пусть функция y = f(x) непрерывна на отрезке [a; b] и F(x) - одна из первообразных функции на этом отрезке, тогда справедлива формула Ньютона-Лейбница: Формулу Ньютона-Лейбница называют основной формулой интегрального исчисления. Для доказательства формулы Ньютона-Лейбница нам потребуется понятие интеграла с переменным верхним пределом. Если функция y = f(x) непрерывна на отрезке [a; b], то для аргумента Действительно, запишем приращение функции Перепишем это равенство в виде Вычислим F(a), используя первое свойство определенного интеграла: Приращение функции принято обозначать как Для применения формулы Ньютона-Лейбница нам достаточно знать одну из первообразных y=F(x) подынтегральной функции y=f(x) на отрезке [a; b] и вычислить приращение этой первообразной на этом отрезке. В статье методы интегрирования разобраны основные способы нахождения первообразной. Приведем несколько примеров вычисления определенных интегралов по формуле Ньютона-Лейбница для разъяснения.
44. Основные методы вычисления определенного интеграла.
|
||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 537; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.131.98.117 (0.012 с.) |


 -дифференцируемые функции, то
-дифференцируемые функции, то  откуда
откуда  Интегрируя последнее выражение, получаем
Интегрируя последнее выражение, получаем
 (1)
(1) (1)
(1) (5)
(5)
 (6)
(6)
 (7)
(7) . (8)
. (8) , где
, где 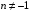 , (2.7)
, (2.7)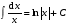 , где
, где  , (2.8)
, (2.8)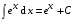 , (2.9)
, (2.9) , где
, где  ,
,  , (2.10)
, (2.10) , (2.11)
, (2.11) , (2.12)
, (2.12) , (2.13)
, (2.13) , (2.14)
, (2.14) , (2.15)
, (2.15) . (2.16)
. (2.16) , где
, где  , можно единственным образом разложить на сумму простейших дробей:
, можно единственным образом разложить на сумму простейших дробей:

 ,
, ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  – некоторые действительные числа.
– некоторые действительные числа. соответствуют простейшие дроби первого и второго типов, а квадратным множителям – третьего и четвертого типов. При этом число простейших дробей, соответствующих данному множителю (линейному или квадратному), равно степени, с которой этот множитель входит в разложение знаменателя дроби. Формула разложения правильной рациональной дроби на простейшие дроби остается справедливой для любого конечного числа линейных и квадратных множителей, входящих в разложение знаменателя
соответствуют простейшие дроби первого и второго типов, а квадратным множителям – третьего и четвертого типов. При этом число простейших дробей, соответствующих данному множителю (линейному или квадратному), равно степени, с которой этот множитель входит в разложение знаменателя дроби. Формула разложения правильной рациональной дроби на простейшие дроби остается справедливой для любого конечного числа линейных и квадратных множителей, входящих в разложение знаменателя 
 .
. .
. .
. .
. этих многочленов были равны. Учитывая это, приравниваем коэффициенты при одинаковых степенях
этих многочленов были равны. Учитывая это, приравниваем коэффициенты при одинаковых степенях  линейных алгебраических уравнений для нахождения
линейных алгебраических уравнений для нахождения  ,
, 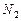 , ….,
, ….,  III.
III. 
 IV.
IV. 


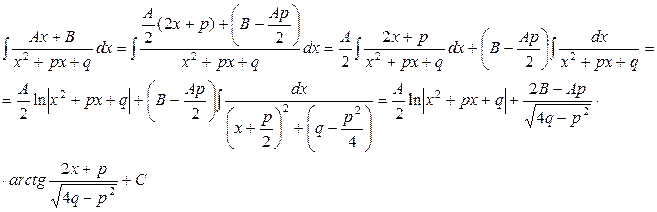
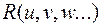 обозначать рациональную функцию относительно
обозначать рациональную функцию относительно  ,
,  ,
,  ,..., т. е. выражение, которое получено из любых величин
,..., т. е. выражение, которое получено из любых величин  . Универсальная подстановка.
. Универсальная подстановка. . Этой подстановкой интеграл
. Этой подстановкой интеграл  , который, как было показано, всегда выражается в элементарных функциях.
, который, как было показано, всегда выражается в элементарных функциях. ,
,  и
и  через
через 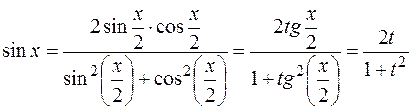 ,
, ,
, ,
,  .
. ,
,  .
. .
. , где p – рациональная дробь, k и b – действительные коэффициенты.
, где p – рациональная дробь, k и b – действительные коэффициенты.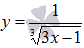 .
. и таблица первообразных сразу приводят нас к ответу:
и таблица первообразных сразу приводят нас к ответу: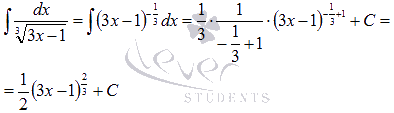
 .
.







 , где х, t – любые буквы.
, где х, t – любые буквы.
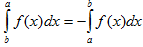


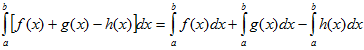
 .
. интеграл вида
интеграл вида  является функцией верхнего предела. Обозначим эту функцию
является функцией верхнего предела. Обозначим эту функцию  , причем эта функция непрерывная и справедливо равенство
, причем эта функция непрерывная и справедливо равенство  .
. , соответствующее приращению аргумента
, соответствующее приращению аргумента  и воспользуемся пятым свойством определенного интеграла и следствием из десятого свойства:
и воспользуемся пятым свойством определенного интеграла и следствием из десятого свойства:
 .
. . Если вспомнить определение производной функции и перейти к пределу при
. Если вспомнить определение производной функции и перейти к пределу при  , то получим
, то получим  . То есть,
. То есть,  , где С – произвольная постоянная.
, где С – произвольная постоянная. , следовательно,
, следовательно,  . Воспользуемся этим результатом при вычислении F(b):
. Воспользуемся этим результатом при вычислении F(b):  , то есть
, то есть  . Это равенство дает доказываемую формулу Ньютона-Лейбница
. Это равенство дает доказываемую формулу Ньютона-Лейбница 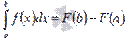 .
. . Пользуясь этим обозначением, формула Ньютона-Лейбница примет вид
. Пользуясь этим обозначением, формула Ньютона-Лейбница примет вид  .
.


