
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Достаточные условия наличия перегибаСодержание книги
Поиск на нашем сайте
1. Если меняет знак при переходе через точку x0, то x0 - точка перегиба. 2. Если то при n четном x0 - точка перегиба, при n нечетном x0 не является точкой перегиба.
31. Асимптоты графика функции. Определение, уравнения асимптот.
Призрак асимптоты давно бродил по сайту чтобы, наконец, материализоваться в отдельно взятой статье и привести в особый восторг читателей, озадаченных полным исследованием функции. Нахождение асимптот графика – одна из немногих частей указанного задания, которая освещается в школьном курсе лишь в обзорном порядке, поскольку события вращаются вокруг вычисления пределов функций, а они относятся всё-таки к высшей математике. Посетители, слабо разбирающиеся в математическом анализе, намёк, думаю, понятен;-) …стоп-стоп, вы куда? Представьте переменную точку, которая «ездит» по графику функции. Асимптота – это прямая, к которой неограниченно близко приближается график функции при удалении его переменной точки в бесконечность. На плоскости асимптоты классифицируют по их естественному расположению: 1) Вертикальные асимптоты, которые задаются уравнением вида 2) Наклонные асимптоты традиционно записываются уравнением прямой с угловым коэффициентом
32. Схема исследования функции и построения ее графика.
Процесс исследования функции состоит из нескольких этапов. Для наиболее полного представления о поведении функции и характере ее графика необходимо отыскать: 1. Область существования функции. Это понятие включает в себя и область значений и область определения функции. 2. Точки разрыва. (Если они имеются). 3. Интервалы возрастания и убывания. 4. Точки максимума и минимума. 5. Максимальное и минимальное значение функции на ее области определения. 6. Области выпуклости и вогнутости. 7. Точки перегиба.(Если они имеются). 8. Асимптоты.(Если они имеются). 9. Построение графика. Применение этой схемы рассмотрим на примере. Пример. Исследовать функцию
Находим область существования функции. Очевидно, что областью определения).¥ (1; È (-1; 1) È; -1) ¥функции является область (- В свою очередь, видно, что прямые х = 1, х = -1 являются вертикальными асимптотами кривой. Областью значений).¥; ¥данной функции является интервал (- Точками разрыва функции являются точки х = 1, х = -1. Находим критические точки. Найдем производную функции
Критические точки: x = 0; x = - Найдем вторую производную функции
Про вертикальные асимптоты было уже сказано выше. Теперь найдем наклонные асимптоты.
Итого, уравнение наклонной асимптоты – y = x. Построим график функции:
33. Первообразная. Неопределенный интеграл. Основные понятия и определения.
Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство
|
|||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 305; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.212.51 (0.009 с.) |

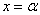 , где «альфа» – действительное число. Популярная представительница
, где «альфа» – действительное число. Популярная представительница  определяет саму ось ординат,
определяет саму ось ординат,  .
.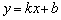 . Иногда отдельной группой выделяют частный случай – горизонтальные асимптоты
. Иногда отдельной группой выделяют частный случай – горизонтальные асимптоты  . Например, та же гипербола с асимптотой
. Например, та же гипербола с асимптотой  .
. и построить ее график.
и построить ее график.
 ; x =; x = -1; x = 1.
; x =; x = -1; x = 1.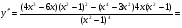


 .
.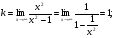


 для любого х из заданного промежутка.
для любого х из заданного промежутка.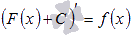 . Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.
. Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.


