
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Последовательность расчета погрешностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Прямых измерений Обобщая изложенное выше, можно предложить следующую схему расчетов результатов нескольких прямых измерений. 1. Вычислить по (2.8) среднее арифметическое 2. Рассчитать по (2.9) абсолютные погрешности 3. Определить по (2.10) среднее арифметическое 4. Отбросить из серии измерений те значения измеренных величин, абсолютная погрешность 5. Повторить п. 1…3 для оставшихся после исключения промахов значений измеренных величин. 6. Определить инструментальную погрешность 7. Если вычисленные 8. Записать окончательный результат:
Довольно часто в лабораторном практикуме проводятся однократные измерения величин. Очевидно, что в этом случае нет возможности рассчитать случайную погрешность измерений Для лучшего усвоения материала рассмотрим конкретный пример расчета абсолютной погрешности прямых измерений. ПРИМЕР 1 С помощью "плотницкого" метра с сантиметровыми делениями была измерена длина l и ширина b комнаты. При трехкратных измерениях получены следующие результаты: l 1=10,00 м; l 2=10,02 м; l 3=9,99 м; || b 1=5,01 м; b 2=5,00 м; b 3=4,98 м. 1. Средние значения измеряемых величин:
2. Абсолютные случайные погрешности каждого из измерений:
3. Средние абсолютные случайные погрешности:
4. Удвоенные абсолютные погрешности длины и ширины составляют 0,024м. Ни одна из погрешностей измерений в п.2 не превышает этого значения. Следовательно, в данных сериях измерений длины и ширины промахи отсутствуют. 5. Инструментальная погрешность измерений "плотницким" метром составляет половину цены деления, т.е.:
6. Случайная и инструментальная погрешности сравнимы, поэтому суммарная абсолютная погрешность равна их сумме:
7. Окончательный результат измерений:
Видно, что в данном примере абсолютные погрешности измерений длины и ширины одинаковы. Возникает вопрос: что же измерено точнее, длина или ширина? Для ответа на этот вопрос воспользуемся понятием относительной погрешности. Рассчитаем ее по (2.2):
Выразим относительную погрешность в процентах:
Отсюда видно, что измерение длины проведено более точно, т.к. абсолютная погрешность длины от самой длины составляет только 0,2%, в то время как абсолютная погрешность ширины по отношению к самой ширине вдвое больше. На этом примере проявляется смысл понятия относительной погрешности: ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ ПОКАЗЫВАЕТ, КАКУЮ ДОЛЮ ОТ САМОЙ ВЕЛИЧИНЫ СОСТАВЛЯЕТ ЕЕ АБСОЛЮТНАЯ ПОГРЕШНОСТЬ. Относительная погрешность является безразмерной величиной. Поэтому с ее помощью можно сравнивать точность не только однородных измерений, как в данном примере (длина и ширина имеют одну единицу измерений - метр), но и неоднородных. Это широко используется при определении погрешностей косвенных измерений. 2.3. ОПРЕДЕЛЕНИЕ ПОГРЕШНОСТЕЙ КОСВЕННЫХ ИЗМЕРЕНИЙ В большинстве случаев при проведении экспериментов не удается непосредственно измерить интересующую нас величину. Чаще всего измеряют другие величины, а затем вычисляют искомую величину, которая является функцией измеренных. Например, необходимо определить площадь комнаты. Комната имеет правильную геометрическую форму, поэтому проще всего получить площадь как произведение длины на ширину. Однако и длина, и ширина комнаты измерены с определенной погрешностью (см. Пример 1). Очевидно, что не может быть рассчитана и точная площадь. Причем величина погрешности площади зависит от точности измерения длины и ширины. Поэтому для определения погрешности расчетной величины необходимо установить взаимосвязь этой погрешности с погрешностями измеренных величин. В данном случае следует вывести формулу, связывающую погрешность площади с погрешностями длины и ширины. ФОРМУЛЫ, СВЯЗЫВАЮЩИЕ ПОГРЕШНОСТИ ВЫЧИСЛЯЕМЫХ ВЕЛИЧИН С ПОГРЕШНОСТЯМИ ИЗМЕРЯЕМЫХ ВЕЛИЧИН, НАЗЫВАЮТСЯ ФОРМУЛАМИ ПОГРЕШНОСТЕЙ. Формулы погрешностей выводятся исходя из РАБОЧИХ ФОРМУЛ, т. е. формул, связывающих вычисляемые величины с измеряемымИ. Один из способов вывода формул погрешностей основан на следующих соображениях. Относительная погрешность величины z по (2.2):
С другой стороны:
Перейдя к небольшим конечным приращениям, (2.19) можно переписать:
Сравнивая (2.18) и (2.20), получаем:
Таким образом, формулу погрешностей можно вывести, взяв дифференциал натурального логарифма рабочей формулы. Поэтому для вывода формулы погрешностей рабочую формулу логарифмируют и полученное выражение дифференцируют. Чтобы погрешность была максимальной, все знаки "минус" меняют на знаки "плюс", вместо значков дифференциала " d " ставят значки абсолютных погрешностей "Δ", над всеми символами измеряемых величин ставят значок "–", означающий, что берутся средние значения этих величин. ПРИМЕР 2 Рабочая формула:
Формула погрешностей:
ПРИМЕР 3 Рабочая формула:
Формула погрешностей:
Чтобы каждый раз при необходимости не выводить формулу грешностей, можно пользоваться табл. 2.2. При выводе формулы погрешностей следует руководствоваться правилом: Таблица 2.2 Простейшие рабочие формулы и соответствующе им формулы погрешностей.
В ОКОНЧАТЕЛЬНУЮ ФОРМУЛУ ПОГРЕШНОСТЕЙ ВХОДЯТ ПОГРЕШНОСТИ ТОЛЬКО ТЕХ ВЕЛИЧИН, КОТОРЫЕ ИЗМЕРЯЮТСЯ В ДАННОМ ЭКСПЕРИМЕНТЕ. Это правило можно обосновать с двух точек зрения. Во-первых, дифференциалы постоянных величин равны нулю (см. Пример 3). Во-вторых, очевидно, что погрешность расчетной величины в первую очередь зависит от погрешностей измерений, т. к. погрешности табличных величин, как правило, много меньше погрешностей измерений в лабораторном практикуме. Расчетную величину, как и результат прямых измерений, представляют с учетом абсолютной погрешности:
Абсолютную погрешность расчетной величины можно легко вычислить, зная среднее значение величины и относительную погрешность, вычисленную по формуле погрешностей. Действительно, из (2.18):
Следует отметить, что приведенные в таблице формулы погрешностей не совсем корректны. Они предполагают максимально возможную погрешность, т. е. случай, когда ошибки измерений всех величин допущены в одну сторону и складываются. На самом деле погрешности измерений различных величин допускаются для одних - в мень-шую, для других - в большую сторону по сравнению со средними значениями. Поэтому суммарная погрешность расчетной величины z будет несколько меньше максимальной, указанной в таблице. Для получения точной формулы погрешностей необходимо каждое слагаемое формулы, взятой из таблицы, возвести в квадрат и из получившегося выражения извлечь квадратный корень. Например, для рабочей формулы
Однако в лабораторном практикуме можно пользоваться и неоткорректированными формулами погрешностей из табл. 3. Последовательность расчета
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 1965; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

 измеряемой величины.
измеряемой величины. результатов отдельных измерений.
результатов отдельных измерений. абсолютных погрешностей.
абсолютных погрешностей. которых вдвое превышает среднюю абсолютную погрешность
которых вдвое превышает среднюю абсолютную погрешность 
 измерений по (2.7) как половину цены деления измерительного инструмента.
измерений по (2.7) как половину цены деления измерительного инструмента. следует их сложить по (2.3). Если указанные выше погрешности отличаются более чем в четыре раза, то меньшей следует пренебречь по (2.4) или (2.6).
следует их сложить по (2.3). Если указанные выше погрешности отличаются более чем в четыре раза, то меньшей следует пренебречь по (2.4) или (2.6). . (2.17)
. (2.17) . Следовательно, суммарная абсолютная погрешность измерений
. Следовательно, суммарная абсолютная погрешность измерений  м; ||
м; ||  м.
м. м; ||
м; ||  м;
м; м; ||
м; ||  м;
м; м; ||
м; || 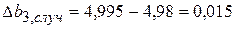 м.
м. м;
м;  м.
м. м; ||
м; || 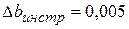 м.
м. м; ||
м; ||  м.
м.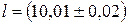 м; ||
м; ||  м.
м. ||
|| 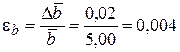
 ||
|| 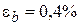
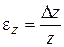 . (2.18)
. (2.18) . (2.19)
. (2.19) . (2.20)
. (2.20) . (2.21)
. (2.21) ,
, ,
, .
. .
. ,
, ,
, (т.к. 4 и π постоянные).
(т.к. 4 и π постоянные). .
.







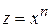


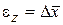






 . (2.22)
. (2.22) . (2.23)
. (2.23)



