
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение случайной погрешностиСодержание книги Поиск на нашем сайте Пусть достаточно точным прибором (настолько, чтобы пренебречь инструментальной погрешностью) проведено n измерений величины х. В результате получено n отличающихся друг от друга значений величины:
Согласно (2.1) находим абсолютные случайные погрешности каждого измерения:
................
Среднее значение абсолютной случайной погрешности измерений:
Равновероятно, что абсолютную случайную ошибку можно допустить как в сторону больших величин по сравнению со средней величиной, так и в сторону меньших. Поэтому результат записывают:
Эта запись обозначает, что истинное значение величины находится в интервале:
Однако такой способ оценки случайной погрешности является приближенным. Теория вероятностей показывает, что основной причиной этого является то, что в общем случае не совсем корректно среднее арифметическое Доверительный интервал при соответствующей ему доверительной вероятности может быть определен методом Стыодента. Для этого сначала определяют дисперсию измерений. Дисперсия D характеризует степень разбросанности результатов измерений относительно истинного значения. Она связана со среднеквадратичным отклонением среднего арифметического S (x) от истинного значения:
Величина, равная доверительному интервалу для
Стьюдентом выведено уравнение, связывающее производную доверительной вероятности Р по t с величиной t:
Графики этих функций приведены на рис. 2.1. Они показывают, что кривые имеют симметричную форму относительно вертикальной оси, проходящей через t = 0, причем крутизна кривых зависит от числа измерений n. Заштрихованная площадь под кривыми дает величину доверительной вероятности Pt, соответствующей отклонению ± t:
Из рис. 2.1 видно, что чем больше количество измерений, тем больше доверительная вероятность при одинаковом отклонении ± t. При постоянной доверительной вероятности с увеличением числа измерений уменьшается отклонение t (рис. 2.1б). Поэтому для уменьшения t, а следовательно и доверительного интервала, следует выполнять возможно большее количество измерений. Значения коэффициентов Стьюдента t для соответствующих доверительных вероятностей Р при различных количествах измерений n сведены в табл. 2.1. Следует отметить, что в лабораторном практикуме обычно расчеты проводят для доверительной вероятности P = 0,95. Найдя коэффициент Стьюдента t пo таблице, величину доверительного интервала вычисляют из (2.14):
Следует отметить, что метод Стьюдента эффективен при большом числе измерений. При типичном для лабораторного практикума
Таблица 2.1 Значения коэффициента Стьюдента t.
числе измерений n < 5 можно ограничиваться расчетом абсолютной погрешности измерений по (2.8)... (2.11). Обнаружение промахов Некоторые значения измеренных величин
|
|||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 228; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.2 (0.006 с.) |

 . Можно показать, что хорошим приближением к истинному значению величины
. Можно показать, что хорошим приближением к истинному значению величины  является среднее арифметическое значение
является среднее арифметическое значение  от всех измеренных значений
от всех измеренных значений  :
: . (2.8)
. (2.8)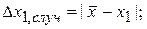
 (2.9)
(2.9) .
. . (2.10)
. (2.10) . (2.11)
. (2.11) . (2.12)
. (2.12) . (2.13)
. (2.13) , выраженному в долях дисперсии, называется коэффициентом Стьюдента:
, выраженному в долях дисперсии, называется коэффициентом Стьюдента: . (2.14)
. (2.14) . (2.10)
. (2.10) .
. . (2.16)
. (2.16)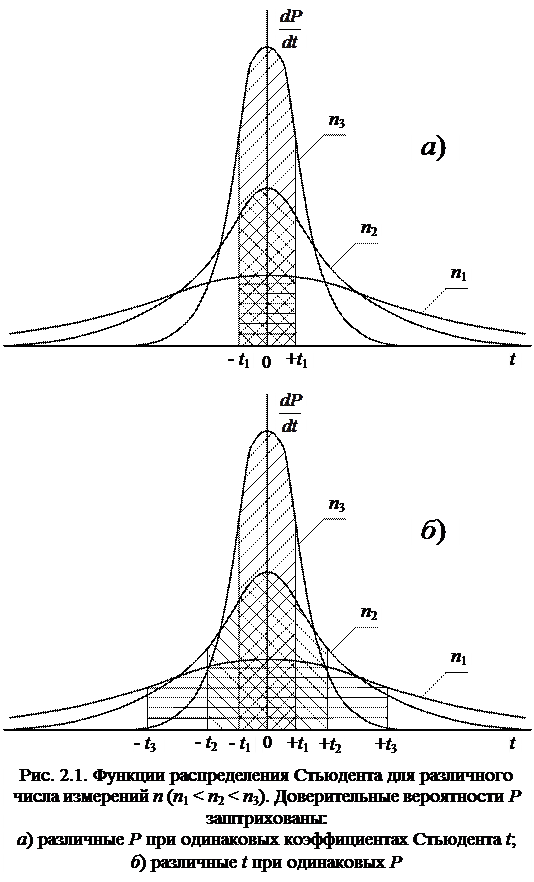
 в серии измерений резко отличаются от остальных. Если их отбросить, считая промахами, то
в серии измерений резко отличаются от остальных. Если их отбросить, считая промахами, то 



