
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основное уравнение молекулярно-кинетической теории идеальных газовСодержание книги
Поиск на нашем сайте
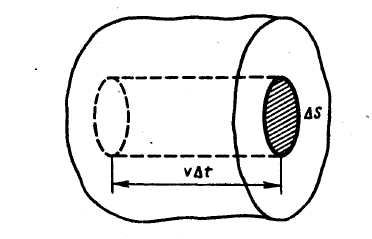
Рассмотрим одноатомный идеальный газ. Предположим, что молекулы газа движутся хаотически, число взаимных столкновений между молекулами газа мало по сравнению с числом ударов о стенки сосуда, а соударения молекул со стенками сосуда абсолютно упругие. Выделим на стенке сосуда некоторую элементарную площадку Δ S и вычислим давление на эту площадку. При каждом соударении молекула, движущаяся перпендикулярно площадке, передает ей импульс m 0 υ -(- m 0 υ) = 2 m 0 υ, где: т 0- масса молекулы, υ - ее скорость.
Необходимо учитывать, что реально молекулы движутся к площадке Δ S под разными углами и имеют различные скорости, причем скорость молекул при каждом соударении меняется. Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных направлений, так что в любой момент времени вдоль каждого из них движется 1/3 молекул, причем половина молекул, т.е. 1/6 часть, движется вдоль данного направления в одну сторону, половина — в противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку Δ S будет 1/6 n Δ Sυ Δ t. При столкновении с площадкой эти молекулы передадут ей импульс Δ P =2 m 0 υ∙ Тогда давление газа, оказываемое им на стенку сосуда, p =Δ Ρ/ (Δ S Δ t) = Если газ в объеме V содержит N молекул, движущихся со скоростями υ 1, υ 2,..., υN, то целесообразно рассматривать среднюю квадратную скорость υ cк= характеризующую всю совокупность молекул газа. Уравнение (3.1) с учетом (3.2) примет вид p= Выражение (7.14) называется основным уравнением молекулярно-кинетической теории идеальных газов. Учитывая, что n=N/V,получим pV= или pV= где W — суммарная кинетическая энергия поступательного движения всех молекул газа. Так как масса газа m=Nm 0, то уравнение (7.14) можно переписать в виде pV= Для одного моля газа т=М (М — молярная масса), поэтому pVm= где Vm — молярный объем. С другой стороны, по уравнению Клапейрона - Менделеева, pVm=RT. Таким образом, RT = откуда υcк = Так как М= NА m 0, где m 0 — масса одной молекулы, а NА — постоянная Авогадро, то из уравнения (7.16) следует, что υcк= где: k=R/NA — постоянная Больцмана. Отсюда найдем, что при комнатной температуре молекулы кислорода имеют υcк =480 м/с, водорода – 1900 м/с. При температуре жидкого гелия те же скорости будут соответственно 40 и 160 м/с. Средняя кинетическая энергия поступательного движения одной молекулы идеального газа < w 0> = пропорциональна термодинамической температуре и зависит только от нее. Из этого уравнения следует, что при N =0 имеем < w 0>=0, т. е. при 0 К прекращается поступательное движение молекул газа, а следовательно, его давление равно нулю. Таким образом, термодинамическая температура является мерой средней кинетической энергии поступательного движения молекул идеального газа, и формула (7.18) раскрывает молекулярно-кинетическое толкование температуры.
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 342; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.254.25 (0.007 с.) |

 n Δ Sυ Δ t =
n Δ Sυ Δ t = 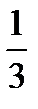 nm 0 υ2 Δ S Δ t.
nm 0 υ2 Δ S Δ t.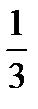 nm 0 υ2. (7.12)
nm 0 υ2. (7.12)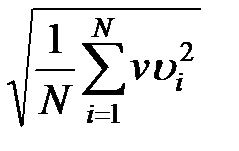 (7.13)
(7.13)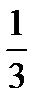 nm 0 υ cк 2. (7.14)
nm 0 υ cк 2. (7.14)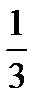 Nm 0 υ cк 2,
Nm 0 υ cк 2, N
N 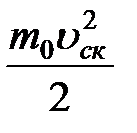 =
= 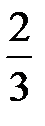 W, (7.15)
W, (7.15) mυ cк 2.
mυ cк 2.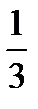 Mυ cк 2
Mυ cк 2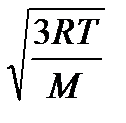 . (7.16)
. (7.16)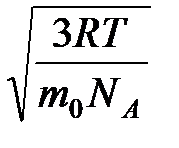 =
= 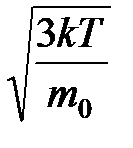 , (7.17)
, (7.17) =
= 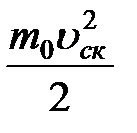 =
=  kТ (7.18)
kТ (7.18)


