
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постулаты специальной (частной) теории относительности
Классическая механика Ньютона прекрасно описывает движение макротел, движущихся с малыми скоростями (υ << c). Однако в конце XIX в. выяснилось, что выводы классической механики противоречат некоторым опытным данным, в частности при изучении движения быстрых заряженных частиц оказалось, что их движение не подчиняется законам механики. Далее возникли затруднения при попытках применить механику Ньютона к объяснению распространения света. Если источник и приемник света движутся друг относительно друга равномерно и прямолинейно, то, согласно классической механике, измеренная скорость должна зависеть от относительной скорости их движения. Американский физик А. Майкельсон в своем знаменитом опыте в 1881 г., а затем в 1887 г. совместно с Е. Морли - опыт Майкельсона - Морли - пытался обнаружить движение Земли относительно эфира (эфирный ветер), применяя интерферометр Майкельсона. Обнаружить эфирный ветер Майкельсону не удалось, как, впрочем, не удалось его обнаружить и в других многочисленных опытах. Опыты «упрямо» показывали, что скорости света в двух движущихся друг относительно друга системах равны. Это противоречило правилу сложения скоростей классической механики. Одновременно было показано противоречие между классической теорией и уравнениями Максвелла, лежащими в основе понимания света как электромагнитной волны. Для объяснения этих и некоторых других опытных данных необходимо было создать новую механику, которая, объясняя эти факты, содержала бы ньютоновскую механику как предельный случай для малых скоростей (υ<< c). Это и удалось сделать А. Эйнштейну, который заложил основы специальной теории относительности. Эта теория представляет собой современную физическую теорию пространства и времени, в которой, как и в классической ньютоновской механике, предполагается, что время однородно, а пространство однородно и изотропно. Специальная теория относительности часто называется также релятивистской теорией, а специфические явления, описываемые этой теорией, - релятивистскими эффектами. В основе специальной теории относительности лежат постулаты Эйнштейна, сформулированные им в 1905 г. I. Принцип относительности:никакие опыты (механические, электрические, оптические), проведенные внутри данной инерциальной системы отсчета, не дают возможности обнаружить, покоится ли эта система или движется равномерно и прямолинейно; все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой.
II. Принцип инвариантности скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета. Первый постулат Эйнштейна, являясь обобщением механического принципа относительности Галилея на любые физические процессы, утверждает, таким образом, что физические законы инвариантны по отношению к выбору инерциальной системы отсчета, а уравнения, описывающие эти законы, одинаковы по форме во всех инерциальных системах отсчета. Согласно этому постулату, все инерциальные системы отсчета совершенно равноправны, т. е. явления (механические, электродинамические, оптические и др.) во всех инерциальных системах отсчета протекают одинаково. Согласно второму постулату Эйнштейна, постоянство скорости света - фундаментальное свойство природы, которое констатируется как опытный факт. 5.3. Преобразования Лоренца
Эти преобразования предложены Лоренцом в 1904 г., еще до появления теории относительности, как преобразования, относительно которых уравнения Максвелла инвариантны. Рассмотрим две инерциальные системы отсчета: К (с координатами x,y, z) и К' (с координатами x′, y′, z′), движущуюся относительно К вдоль оси x со скоростью Преобразования Лоренца в этом случае имеют вид К x′ = y′ = y, y = y′, (5.5) z′ = z, z = z′, t′ =
Из сравнения приведенных уравнений вытекает, что они симметричны и отличаются лишь знаком при
Из преобразований Лоренца вытекает также, что при малых скоростях (по сравнению со скоростью света), они переходят в классические преобразования Галилея. Из преобразований Лоренца следует очень важный вывод о том, что как расстояние, так и промежуток времени между двумя событиями меняются при переходе от одной инерциальной системы отсчета к другой, в то время как в рамках преобразований Галилея эти величины считались абсолютными, не изменяющимися при переходе от системы к системе. Таким образом, теория Эйнштейна оперирует не с трехмерным пространством, к которому присоединяется понятие времени, а рассматривает неразрывно связанные пространственные и временные координаты, образующие четырехмерное пространство-время.
5.4. Следствия из преобразований Лоренца Длительность событий в разных системах отсчета. Пусть в некоторой точке (с координатой х), покоящейся относительно системы К, происходит событие, длительность которого (разность показаний часов в конце и начале события) τ = t 2 – t 1, где индексы 1 и 2 соответствуют началу и концу события. Длительность этого же события в системе К′ τ' = t' 2 - t′ 1,(5.6) причем началу и концу события, согласно (5.5), соответствуют t′ 1 = Подставляя (5.7) в (5.6), получаем τ′ = (t2 – t 1)/ Из соотношения (5.8) вытекает, что τ < τ ', т. е. длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе отсчета, относительно которой эта точка неподвижна. Этот результат может быть еще истолкован следующим образом: интервал времени τ ', отсчитанный по часам в системе К', с точки зрения наблюдателя в системе К, продолжительнее интервала τ, отсчитанного по его часам. Следовательно, часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоящихся часов, т. е. ход часов замедляется в системе отсчета, относительно которой часы движутся. Длина тел в разных системах отсчета. Рассмотрим стержень, расположенный вдоль оси х' и покоящийся относительно системы К'. Длина стержня в системе К' будет l′ 0 = x′ 2 - х' 1, где х' 1и x′ 2 - не изменяющиеся со временем t′ координаты начала и конца стержня, а индекс 0 показывает, что в системе отсчета К' стержень покоится. Определим длину этого стержня в системе К, относительно которой он движется со скоростью υ. Для этого необходимо измерить координаты его концов х 1и x 2в системе К в один и тот же момент времени t. Их разность l = х 2 – x 1и даст длину стержня в системе К. Используя преобразования Лоренца (5.5), получим l′ 0 = x′ 2 - х' 1 = Таким образом, длина стержня, измеренная в системе, относительно которой он движется, оказывается меньше длины, измеренной в системе, относительно которой стержень покоится. Если стержень покоится в системе К, то, определяя его длину в системе К', опять-таки придем к выражению (5.9). Из выражения (5.9) следует, что линейный размер тела, движущегося относительно инерциальной системы отсчета, уменьшается в направлении движения в
|
|||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 213; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.131.110.169 (0.011 с.) |
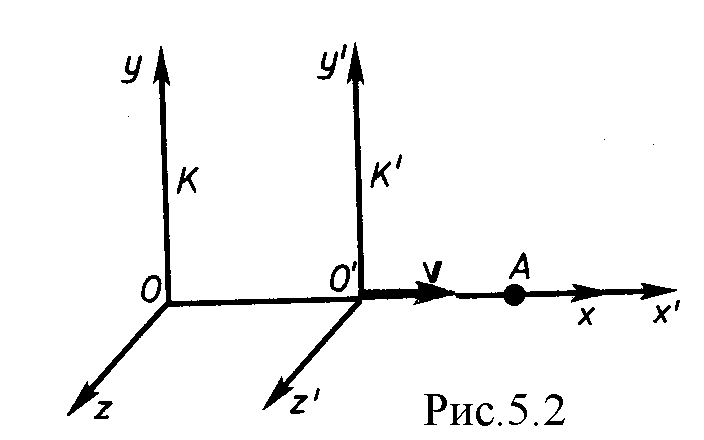 Анализ явлений в инерциальных системах отсчета, проведенный А. Эйнштейном на основе сформулированных им постулатов, показал, что классические преобразования Галилея несовместимы с ними и, следовательно, должны быть заменены преобразованиями, удовлетворяющими постулатам теории относительности.
Анализ явлений в инерциальных системах отсчета, проведенный А. Эйнштейном на основе сформулированных им постулатов, показал, что классические преобразования Галилея несовместимы с ними и, следовательно, должны быть заменены преобразованиями, удовлетворяющими постулатам теории относительности. = const (рис.5.2).
= const (рис.5.2). К' К′′
К' К′′  , x =
, x =  ,
, , t =
, t =  ,
, β = υ / c.
β = υ / c. . Это очевидно, так как если скорость движения системы К' относительно системы К равна
. Это очевидно, так как если скорость движения системы К' относительно системы К равна  , то скорость движения К относительно К' равна (-
, то скорость движения К относительно К' равна (- 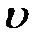 ).
). , t′ 2 =
, t′ 2 = 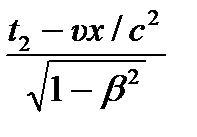 .
. 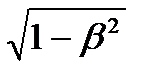 = τ /
= τ / 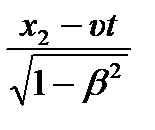 -
-  =
=  = l/
= l/  . (5.9)
. (5.9)


