Геометрична алгебра та перші нерозв’язні задачі

В грецькій матем, зокрема в Піфагорійській школі звернули увагу на відношення між геометрією і арифметикою. Арифметика базувалась на понятті цілого числа. Раціональні числа представлялись як пара цілих. Після того як вияснилось, що відношення 2-х відрізків, загалом не може бути виражено за допомогою відношення цілих чисел, матем с-ма піфагорійців була зруйнована. І вже у самій піф. школі почалась побудова алгебри на основі геометрії, так званої геометричної алгебри. Геометрична мова стала застосовуватись у теорії чисел: зображення чисел точками, розташованих у вигляді правильних фігур було замінено тим що всі числа представлялись відрізками. Основними об’єктами геом. Алгебри були відрізки і прямокутники, а також паралелепіпеди. Додавання відрізків здійснювалось шляхом приєднання одного до іншого, віднімання – шляхом відкидання із більшого відрізка меншого. Множенням 2-х відрізків вважалось побудова прямокутника, 3-х – паралелепіпед, множення більшого числа не розгядалось. Геометрична алгебра була викладена в 2 книзі «Початки» Евкліда і в працях Архімеда і Аполонія. Геометрична алгебра дозволила вперше довести деякі властивості алгебраїчних операцій. Геом. Алгебра була основана на античній планіметрії і представляла собою геометрію циркуля і лінійки. Тому вона була максим адаптована для дослідження тотожностей, обидві частини яких є квадратичними формами, і для роз квадратних рівнянь. Цим по суті і обмежувалось коло застосування геом. алгебри. Згодом з’явились перші задачі, які не вдавалось розв за допомогою циркуля і лінійки. В 5 ст до н.е були поставлені 3 задачі.

Подвоєння куба. Побудувати куб об’єм якого був би вдвічі більший об’єма заданого куба. Першого успіху у розв задачі досяг Гіпократ Хіоський, він звів її до пошуку 2-х середніх пропорцій між заданими величинами. Згодом Архит Тарентський показав що можна розв за допом перетину 3-х поверхонь –конуса, циліндра і тора.

Трисекція кута. Потрібно розділити кут на 3 рівних частини. В історії античної матем для її розв було застосовано метод «вставки» і введена 1-ша трансцендентна крива – квадратиса.

Квадратура круга. Пошук квадрата, який рівновеликий даному кругу.Цю задачу розглядали у 2-х аспектах точному і наближеному. Останній підхід до задачі привів до введення наближення площі круга вписаним або описан многокутником і до наближеного обчислення числа П. Повне трактування задачі можна отримати тільки в результаті вияснення арифметичної природи числа П. розвя’язання цієї задачі розтягнулось на багато віків.

 

11.Римська імперія. Хоча вже в римський час були відомі позиційні системи числення, які були більш досконалими і нагадували сучасну десяткову систему, консервативні римляни воліли користуватися традиційною системою рахунку, в якій числа записувалися як послідовності повторюваних букв.

Для практичних обчислень (зокрема, основних арифметичних дій) римська система числення не підходила. З цією метою використовувалася лічильна дошка (абак), за допомогою якої позначалися одиниці, десятки, сотні й інші розряди чисел. Таким чином, не тільки інженери та техніки, а й комерсанти, ремісники і ринкові торговці мали можливість легко робити елементарні обчислення.

Для повсякденних (наприклад, торгових) обчислень римляни створили переносний варіант абака з бронзи, який легко поміщався в сумці і дозволяв за допомогою невеликих камінчиків виробляти не тільки основні арифметичні дії, а й обчислення з дробами. В принципі, абак можна було використовувати в рамках будь-якої системи числення. Особливий успіх римлян полягав у стандартизації неозорого числа можливих дробів, які могли знайти застосування у світі торгівлі — унція була приведена до єдиного значення.

У римському світі для монет, мір і ваг використовувалася дванацяткова система, яка спочатку з'явилася в Єгипті і Вавилоні, була поширена по всьому Середземномор'ю і досягла Риму завдяки фінікійським купцям і грецьким колоністам Південної Італії. Поряд з вимірюванням ваги в унціях для цієї системи були характерні також дроби з знаменником 12, що спрощувало дії з дробами. У якості «проміжної пам'яті» при множенні або розподілі великих чисел часто служили загнуті фаланги пальців рабів, які таким чином служили своїм господарям підручним засобом для фіксації чисел.

У той час як комерсанти, ремісники і техніки виробляли обчислення за допомогою унцій, в деяких областях були звичайними більш точні міри ваги. Наприклад, у сфері точної механіки і при прокладці труб використовувався палець, що становив 1/16 фута.

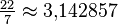В інших областях римляни також демонстрували інтерес насамперед до практичного застосування математичних знань: так, вони знали наближене значення π і використовували його крім іншого для обчислення перерізів труб. Римські землеміри, незважаючи на просту конструкцію їх приладів, могли визначати кути, підйоми і нахили.