
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Індивідуальна самостійна робота «Границя функції. Похідна елементарних функцій».Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Завдання для самостійної роботи А 1. Користуючись означенням похідної, знайдіть похідну функції f, якщо: a) б) в) г) 2. Користуючись означенням похідної, знайдіть похідну функції f, якщо: а) б) в) г) 3. Знайдіть миттєву швидкість руху точки, якщо: а) б) в) г) 4. Рух точки відбувається за законом У який момент часу швидкість руху дорівнює: а) 0; б) 10? 5. Запишіть рівняння дотичної до параболи y= 3x2 - 2 у точці а) x0= -2; б) x0= 0; в) x0= 1. Б
В 1. Знайти координати точки дотику дотичної
2. Знайти кутовий коефіцієнт дотичної до косинусоїди
3. Знайти рівняння дотичної до графіка функції а) в) ТЕМА: ДИФЕРЕНЦІЮВАННЯ ФУНКЦІЙ ПЛАН:
Правила диференціювання. Теорема: Якщо функції u(x) і n(x) мають похідні у всіх точках інтервалу (a; b), то (u(x)±(x))’ = u’(x)±n’(x) для любого х є (a; b). Коротше, (u±n)’ = u±n’ Доведення: Суму функцій u(x)+n(x), де х є (a; b), яка представляє собою нову функцію, позначимо через f(x) і знайдемо похідну цієї функції, Нехай х0 – деяка точка інтервалу (a; b).
Тоді
Також, Так як х0 – допустима точка інтервалу (a; b), то маємо:
Випадок добутку розглядається аналогічно. Теорема доведена. Наприклад, а) б) в) Зауваження. Методом математичної індукції доводиться справедливість формули (u1(x) + u2 (x) +… кінцевого числа складених. Теорема. Якщо функції u(x) і n(x) мають похідні у всіх точках інтервалу (a; b), то
для любого х є (a; b). Коротше,
Доведення. Позначимо похідні Нехай х0 – деяка точка інтервалу (a; b). Тоді
Навіть так як
то
Так як х0 – вільна точка інтервалу (a; b), то маємо
Теорема доведена. Приклад, а) б) в)
Наслідок. Постійний множник можна виносити за знак похідної:
Доведення. Застосувавши множник можна виносити за знак теорему про похідну де а – число, отримаємо
Приклади. а) б) Похідна частки двох функцій. Теорема. Якщо функції
Доведення. Позначимо тимчасово Нехай х0 – деяка точка інтервалу (a; b). Тоді,
Навіть, так як
і послідовно
Так як х0 – вільна точка інтервалу (a; b), то в останній формулі х0 можна замінити на х. Теорема доведена. Приклади. а) б) Основні правила диференціювання. Нехай u(x), v(x), – диференційовані в точці х функції, С –стала.
Похідна складної функції. Якщо функція y = f (u) має похідну в точці u, а функція u = g (x) – в точці x, то складена функція y = f (g (x)) диференційована в точці x, причому y ' = f ' (u) ∙ g ' (x). Іншими словами, похідна складеної функції y = f (u), u = g (x) дорівнює добутку похідної від зовнішньої функції, взятої по внутрішньому аргументу u, і похідної від внутрішньої функції, взятої по незалежній змінній x. Якщо u (x) - диференційовна в точці x функція, то виконуються такі формули диференціювання складених функцій:
Розглянемо приклад. Приклад 1. Нехай треба обчислити по заданому значенню χ значення функції у, яка задана формулою у = Для цього спочатку треба обчислити за заданим значенням х значення u = g(x) = 9 – x2, а потім за значенням u обчислити у = f(u) = Отже, функція g ставить у відповідність числу x число u, а функція f — числу u число у. Говорять, що у є складеною функцією із функцій g і f, і пишуть у = f(g(x))· Функцію g(x) називають внутрішньою функцією, або проміжною змінною, функцію f(u) — зовнішньою функцією. Отже, щоб обчислити значення складеної функції у = f(g(x)) в довільній точці х, спочатку обчислюють значення й внутрішньої функції g, а потім f(u). Приклад 2. Розглянемо функцію у = Приклад 3. Запишіть складені функції f(g(x)) і g(f(x)), якщо f(x) = sin х, g(x) = x2. Розв'язання f(g(x)) = sin g(x) = sin x 2; g(f(x)) = (f(x))2 = (sinx)2 = sin2 х. Виконання вправ 1. Задайте формулами елементарні функції f і g, із яких побудована складена функція у = f(g(x)): а) у = cos (2 х + 3); б) у = (2x + 3)7; в) у = Відповіді: а) u = g(х) = 2х + 3; y = f(u) = cos u; б) и = g(x) =2х+3; у = f(u) = u7; в) u = g(x) =х2 +2х; у = f(и) = У складеній функції у = f(g(x)) присутня проміжна змінна u =g(x). Тому при знаходженні похідної складеної функції ми будемо вказувати, по якій змінній взято похідну, використовуючи при цьому спеціальні позначення:
Приклад 1. Знайдіть похідну функції у = (3 x 3 – 1)5. Розв'язання у = (3х3 – 1)5 — складена функція у = u5, де u = 3x3 – 1, тоді При обчисленні похідної складеної функції явне введення допоміжної букви u для позначення проміжного аргументу не є обов'язковим. Тому похідну даної функції знаходять відразу як добуток похідної степеневої функції u5 на похідну від функції 3 х 3 – 1: у' = ((3 x 3 – 1)5)' = 5(3х3 -1)4 · (3 x 3 – 1)' = 5 · (3 x 3 – 1)4 · 9 x = 45 x (3 x 3 – 1)4. Приклад 2. Знайдіть похідні функцій: а) у = Розв'язання
б) у' = (sin(3x + 5))' = cos (3х + 5) · (3x· + 5)' = 3 cos(3x + 5);
в) у = (cos2 x)' = 2 cos x · (cos x)' = 2 cos x · (- sin x) = = -2 cos x sin x = - sin 2x; г) y’ = (cos x2)' = - sin x2 · (x2)' = -2x sin x2.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 540; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.009 с.) |

 ;
2.
;
2.  3.
3.  4.
4.  5.
5.  6.
6.  7.
7.  8.
8.  9.
9.  10.
10.  11.
11.  12.
12. 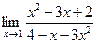 13.
13.  14.
14.  15.
15.  16.
16.  17.
17.  18.
18. 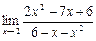 19.
19.  20.
20.  21.
21.  22.
22.  23.
23. 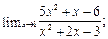 24.
24.  25.
25.  26.
26. 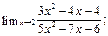 27.
27. 
 , xo =1;
2.
, xo =1;
2.  , xo = -2;
3.
, xo = -2;
3.  , xo = 2;
4.
, xo = 2;
4.  , xo = 3;
5.
, xo = 3;
5.  , xo = - 3;
6.y = 3 x 3 – 3 x 2 + 3, xo = - 1;
7.y =
, xo = - 3;
6.y = 3 x 3 – 3 x 2 + 3, xo = - 1;
7.y = 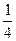 x 4 – x 2 – 4, xo = - 4;
8.у = 2 x 3 – 3 x 2 – 12 x + 3, xo =1;
9.y =3 x 3 –5 x 2 + 4 х, xo = -2;
10.y = x 4 – 2х +5, xo = - 1;
11.
x 4 – x 2 – 4, xo = - 4;
8.у = 2 x 3 – 3 x 2 – 12 x + 3, xo =1;
9.y =3 x 3 –5 x 2 + 4 х, xo = -2;
10.y = x 4 – 2х +5, xo = - 1;
11.  , xo = -2;
12.
, xo = -2;
12.  , xo = -3;
13.
, xo = -3;
13.  , xo = -2;
14.
, xo = -2;
14.  , xo = -2;
15.
, xo = -2;
15.  , xo = - 1;
16.
, xo = - 1;
16.  , xo = 1;
17.
, xo = 1;
17.  , xo = -1;
18.
, xo = -1;
18. 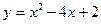 , xo = -3;
19.
, xo = -3;
19.  , xo = 2;
20.
, xo = 2;
20.  , xo = -3;
21.
, xo = -3;
21. 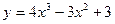 , xo = - 3;
22.y = x 3 – 4 x 2 + 7, xo = - 1;
23.y = x 2 – 8 x – 4, xo = 3;
24.у = 4 x 3 + x 2 – 5 x + 3, xo = -1;
25.y = x 3 –3 x 2 + 2, xo = -2;
26.y = 2 x 3 – 4х +6, xo = - 1;
27.y = 5 x 3 + 3х -3, xo = -2
, xo = - 3;
22.y = x 3 – 4 x 2 + 7, xo = - 1;
23.y = x 2 – 8 x – 4, xo = 3;
24.у = 4 x 3 + x 2 – 5 x + 3, xo = -1;
25.y = x 3 –3 x 2 + 2, xo = -2;
26.y = 2 x 3 – 4х +6, xo = - 1;
27.y = 5 x 3 + 3х -3, xo = -2
 ;
2.у=cosx; у=x ∙ x6
3.у=lnx; у= -arctgx;
4.у= - х; у= 5х ;
5.у=sinx; у=7x
6.у=x-3; у= 3х ;
7.у=х9 ; у= -arcctgx;
8.у=arccosx; у=
;
2.у=cosx; у=x ∙ x6
3.у=lnx; у= -arctgx;
4.у= - х; у= 5х ;
5.у=sinx; у=7x
6.у=x-3; у= 3х ;
7.у=х9 ; у= -arcctgx;
8.у=arccosx; у=  ;
9. у=e x ; у=13x;
10. у=5; у=x -3 ∙ x6
11. у=log4x; у=
;
9. у=e x ; у=13x;
10. у=5; у=x -3 ∙ x6
11. у=log4x; у=  12. у=arcsinx; у=
12. у=arcsinx; у=  ;
13. у=х -5; у= lоg8x;
14. у= -lnx; у=x3 ∙ x6
15. у= 2х ; у=x3 ∙ x -2
16. у=х 8; у= 7х ;
17. у=lgx; у=x -8 ∙ x6
18. у=arctgx; у=
;
13. у=х -5; у= lоg8x;
14. у= -lnx; у=x3 ∙ x6
15. у= 2х ; у=x3 ∙ x -2
16. у=х 8; у= 7х ;
17. у=lgx; у=x -8 ∙ x6
18. у=arctgx; у=  ;
19. у=-4х; у=
;
19. у=-4х; у=  20. у=10x; у=log7x;
21. у=arcctgx; у=
20. у=10x; у=log7x;
21. у=arcctgx; у=  ;
22. у=
;
22. у=  ; у=log15x;
23. у=- lgx; у=x6 ∙ x9
24. у= - cosx; у=x6 ∙ x6
25. у=-8; у= 11х ;
26. у=
; у=log15x;
23. у=- lgx; у=x6 ∙ x9
24. у= - cosx; у=x6 ∙ x6
25. у=-8; у= 11х ;
26. у=  ; у=log11x;
27. у=log7x; у=
; у=log11x;
27. у=log7x; у=  ;
;
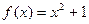 в точці 1;
в точці 1; в точці 1;
в точці 1;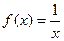 в точці 1;
в точці 1; в точці 1.
в точці 1. ;
;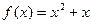 ;
;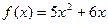 ;
;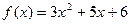 .
. ;
;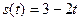 ;
; ;
; .
.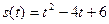 .
. у точці перетину кривої з віссю абсцис.
у точці перетину кривої з віссю абсцис.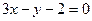 є рівнянням дотичної до її графіка в точці А(1;1): a)
є рівнянням дотичної до її графіка в точці А(1;1): a)  ; б)
; б)  ; в)
; в)  ; г)
; г) 
 ; б)
; б) 
 , де s – шлях у метрах, t – час у секундах. Знайти пройдений шлях у той момент, коли швидкість дорівнює нулю.
, де s – шлях у метрах, t – час у секундах. Знайти пройдений шлях у той момент, коли швидкість дорівнює нулю. до кривої, заданої рівнянням
до кривої, заданої рівнянням .
. у точці з абсцисою
у точці з абсцисою  .
. в точці з абсцисою x = x0:
в точці з абсцисою x = x0: ; б)
; б)  ;
;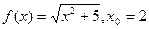 .
.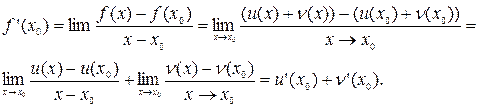








 через
через  х є (a; b), і найдемо похідну цієї функції, виходячи із визначення.
х є (a; b), і найдемо похідну цієї функції, виходячи із визначення.
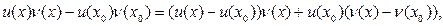






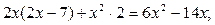

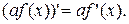


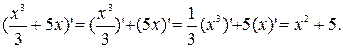
 мають похідні у всіх точках інтервалу (a; b), причому
мають похідні у всіх точках інтервалу (a; b), причому  для любого х є (a; b), то
для любого х є (a; b), то для любого х є (a; b).
для любого х є (a; b).
 через
через  знайдемо
знайдемо 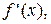 використовуючи визначення похідної.
використовуючи визначення похідної.
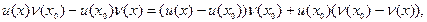 то
то




 ;
; 
 ;
; 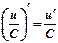 ;
; 
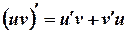 ;
; 


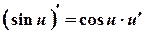

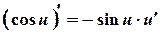












 .
. .
. . Вона є складеною із функцій u = cos х, у =
. Вона є складеною із функцій u = cos х, у =  ; г) у = sin2 x.
; г) у = sin2 x. — похідна функції у по аргументу x;
— похідна функції у по аргументу x; — похідна функції у по аргументу u;
— похідна функції у по аргументу u; — похідна функції u по аргументу x.
— похідна функції u по аргументу x.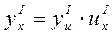 y' = (u5)' · (3х3 – 1)’ = 5u4 · 9х = 5(3х3 -1)4 · 9х = 45х(3х3 – 1)4.
y' = (u5)' · (3х3 – 1)’ = 5u4 · 9х = 5(3х3 -1)4 · 9х = 45х(3х3 – 1)4. ; б) у = sin (3х + 5); в) у = cos2x; г) y = cos x2.
; б) у = sin (3х + 5); в) у = cos2x; г) y = cos x2.



