
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інваріантність форми диференціала.Содержание книги
Поиск на нашем сайте
Правило знаходження похідної функції від функції (складної функції) має можливість одержати важливу власність диференціала. Нехай функції y = f (x) i x =
Диференціал dy, коли х вважати незалежною змінною, визначається за формулою dy = уx '·dx. Перейдемо тепер до незалежної змінної t: y цьому випадку маємо другий вираз для диференціала dy = yt'·dt. Заміною похідної уt' її виразом (8) одержимо
тому Отже, канонічний вираз диференціала функції виявляється справедливим незалежно від вибору останнього аргументу (незалежної змінної). Канонічний вираз диференціала функції залишається незмінним при різному доборі аргументу. Ми завжди можемо записати диференціал dx y вигляді: dy = yx'dx не дивлячись на те, чи буде х незалежною змінною, чи ні; різниця лише в тому, що якщо за незалежну змінну вибране t. То dx не довільний приріст Застосування до наближених обчислень. При досить малому прирості х аргументу
якщо позначити
Таким чином, для значення де, близьких до х0, функцію f (x) наближено можна замінити лінійною функцією. Геометричне це заміні ділянки кривої y=f(x), прилеглої до точки (x0,f(x0), відрізком дотичної до кривої в цій точці:
(див. Рис. 1). Беручи значення х0 = 0 і обмежуючись малими значеннями х, одержимо наближену формулу
Звідси, підставляючи замість f (x) різні елементарні функції, легко одержати ряд формул
Приведемо декілька прикладів. Приклад 1. Обчислимо наближено sin 46°. Розв’язання: Приймемо за початкове значення незалежної змінної х0 = 45° =
Приклад 2. Обчислити наближено Розв’язання: Розглянемо функцію
Приклад 3. Обчислити наближено Розв’язання: Перетворимо вираз, що стоїть під знаком радикала:
При обчисленні Формула запишеться так: Інакше Підставивши (2) у рівність (1), дістанемо
Приклад 4. Наближено обчислити значення Розв’язання. В даному випадку Нехай
Приклад 4. Наближено обчислити значення ln 0,97. Розв’язання.
Приклад 4. Наближено обчислити значення (3,045)5. Розв’язання.
|
||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 1083; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.129.241 (0.005 с.) |

 (t) такі, що з них можна одержати складну функцію y = f (
(t) такі, що з них можна одержати складну функцію y = f ( (8)
(8) але
але  (9)
(9)
 х, а диференціал dx як функцію від t. Цю властивість і називають інваріантність форм.
х, а диференціал dx як функцію від t. Цю властивість і називають інваріантність форм. або
або  (10)
(10) або
або  (11)
(11)


 (наприклад
(наприклад  );
);

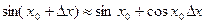

 , а за
, а за  . Тоді згідно (11)
. Тоді згідно (11)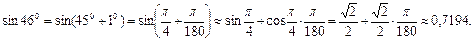
 .
. і приймемо за початкове значення незалежної змінної x0 = 4, а за
і приймемо за початкове значення незалежної змінної x0 = 4, а за 
 .
.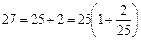 , звідки
, звідки  . (1)
. (1) введемо функцію
введемо функцію  , тоді
, тоді  .
. .
. . (2)
. (2) .
. .
. .
. ,
,  , тоді
, тоді  і за формулою:
і за формулою:  , отримаємо, що:
, отримаємо, що: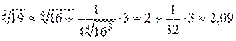 .
. .
.




