
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Миттєва швидкість прямолінійного рухуСтр 1 из 7Следующая ⇒
Границя функції в точці.
g(x) = Функція g(x) = Якщо х наближається до 1 (зліва чи справа), то у наближається до 2 (відповідно знизу чи зверху).
Розглянемо третій приклад. Побудуємо графік функції
При х → 1 (що наближається до 1) границі функції h(x) не існує, поскільки не існує єдиного числа, до якого наближається функція при х, що прямує до 1. (Якщо х наближається до 1 зліва, то h(x) наближається до 1; якщо ж х наближається до 1 справа, то h(x) наближається до 2). Таким чином: Якщо при значеннях х, що прямують до деякого числа а, значення функції f(x) прямують до єдиного значення b, то говорять, що при х, що наближається до а, функція f(x) має границю, яка дорівнює b, і це записується так: Нехай задано деяку функцію, наприклад, f(x) = 2х + 1. Розглянемо таблицю значень цієї функції в точках, що досить близько розташовані до числа 1 (і в самій точці 1), та знайдемо |х – 1| та |f(x) – 3| у відповідних точках.
З таблиці видно, що при наближенні значення аргументу до числа 1 значення функції наближається до числа 3, при цьому похибка значень функції може бути досягнена як завгодно малою, шляхом зменшення похибки аргументу. Дійсно, взявши довільне ε > 0, тоді |f(x) – 3| < ε,
Отже, щоб похибка значень функції не перевищувала ε > 0, слід взяти значення х такі, що |х – 1| < О Число b називається границею функції у = f(x) в точці а, якщо для будь-якого ε > 0 існує таке число δ = δ(ε) > 0, що для всіх х: 0 < |х – а| < δ, виконується нерівність |f(x) – b| < ε. (Рис. 13). Приклад. Доведіть, що Розв'язання Задамо довільне ε > 0 і покажемо, що існує δ > 0 таке, що із нерівності |х - 3| < δ випливає нерівність |(2х - 1) - 5| < ε. Маємо |(2х - 1) - 5| < є, |2х - б| < ε; |2(х - 3)| < ε; 2·|х - 3| < ε; |х - 3| <
| x - 3| < δ приведе до виконання нерівності |(2x - 1) - 5| < ε. Отже, згідно з означенням границі маємо: Основні теореми про межу. теореми, які ми приймемо без доведення. 1. Якщо функція f(x) має границю при х → а, то ця границя єдина. 2. Границя постійної функції дорівнює постійній 3. Границя суми (різниці) двох функцій дорівнює сумі (різниці) їхніх границь, при умові, що границі доданків існують.
4. Границя добутку двох функцій дорівнює добутку границь цих функцій, якщо границі множників існують
5. Постійний множник можна виносити за знак границі
6. Границя частки двох функцій дорівнює частці границь цих функцій, якщо границі чисельника і знаменника існують і границя знаменника не дорівнює нулю
Сформульовані теореми використовуються при знаходженні границь функцій.
Приклад 1. Знайдіть
Розв'язання
Відповідь: 3. Приклад 2. Знайдіть Розв'язання
Відповідь: 2. Приклад 3. Знайдіть Розв'язання В цьому прикладі безпосередньо скористатися теоремами про границі не можна, бо границя знаменника дорівнює нулю. Оскільки в означенні границі |х – а| > 0, тобто |х — а|
Відповідь: 4. Приклад 4. Знайдіть Розв'язання
Відповідь: – 1.
Перша чудова границя Приклад. Знайти Розв'язання
Відповідь: 7.
Розкриття невизначеностей Перш ніж перейти к обчисленню границь, запишемо за допомогою символів основні теореми теорії границь. Нагадаємо символи: a – стала ∞ - нескінченна велика додатня -∞ - нескінченна велика від’ємна +0 – нескінченна мала додатня -0 – нескінченна мала від’ємна 1) a +0= a; a ∙ 0=0; 2) 3) a +∞=∞; a ∙ ∞=∞; ∞+∞=∞; ∞ ∙ ∞=∞ 4) ∞∞=∞; 0 ∙ ∞=∞
Але при обчисленні границь дуже часто з’являються так названі невизначеності. Символічно їх можна записати так:
Ці умовні записи характеризують поведінку змінних величин. Щоб знайти границю невизначеності виразу, треба усунути цю невизначеність.
Розглянемо деякі окремі випадки. 1) Невизначеність виду
= Тобто, щоб розкрити невизначеність 1. Якщо найвищий степінь чисельника вище найвищого степеня знаменника, то границя дробу нескінченно велика. 2. Якщо найвища степінь чисельника нижче найвищого степеня знаменника, то границя дробу дорівнює нулю. 3. Якщо найвищі степені чисельника і знаменника однакові, то границя дорівнює частки від поділу коефіцієнтів біля старших степенів. 2) Невизначеність виду
Розкладемо чисельник і знаменник на множини:
Множини (x-1), через який чисельник і знаменник прямують до нуля, називають критичним множником. Таким чином, щоб розкрити невизначеність 3) Невизначеність
(х-2) – критичний множник. Позбудемося від ірраціональності в чисельнику.
4) Невизначеності виду ∞-∞ задані ірраціональними виразами.
Матеріальної точки.
S=0S0= f(t0 )S1= f(t1 ) S t=0 t0 t1 ЗАДАЧА1. Нехай матеріальна точка М рухається прямолінійно по закону s=f (t). В момент часу t0 вона зайняла положення М0 і пройшла шлях s0 =f (t0). Знайдемо швидкість точки в момент часу t0. Припустимо, що за довільно вибраний проміжок часу ∆t, починаючи з моменту t0, точка перемістилась на відстань ∆s і зайняла положення М1. Тоді t1 = t0 + ∆t, s1 = f (t1) = s0 + ∆ s.
За проміжок часу ∆t матеріальна точка проходить шлях ∆x = f (t1) - f (t0) = f (t0 + ∆t) - f (t0).
Середня швидкість Vсер. руху на проміжку М0М1 дорівнює:
Vсер. = Якщо проміжок ∆t буде зменшуватися, то ця величина буде більш точніша. Таким чином, можна вважати, якщо ∆t наближається до нуля, то середня швидкість Vсер. буде наближатися до швидкості в момент часу t0. О1 . Миттєвою швидкістю точки, яка рухається прямолінійно, в момент часу t0 називається границя середньої швидкості при умові, що t наближається до нуля. V мит . = Числа ∆t, ∆s називаються відповідно приростом часу, приростом шляху. Отже, миттєвою швидкістю точки, яка рухається прямолінійно, є границя відношення приросту шляху ∆ s до відповідного приросту часу ∆ t, коли приріст часу наближається до нуля. Дотична до кривої
Розглянемо функцію y = f (x) і її графік – криву лінію. АМ – січна. Зафіксуємо точку А. Нехай точка М, рухаючись по кривій, наближається до точки А.При цьому січна АМ буде повертатися навколо точки А і в граничному положенні при наближенні точки М до точки А січна займе положення прямої АТ. Пряму АТ називають дотичною до даної кривої в точці А.
О2. Дотичною АТ до графіка функції y = f (x) в точці А називається граничне положення січної АМ, коли точка М, рухаючись по кривій, наближається до точки А.
ЗАДАЧА 2. Провести дотичну до графіка функції y = f(x) в точці А(x0;y0). Положення прямої y= kx+b визначається кутовим коефіцієнтом прямої k = tg a, де a – кут між прямою і додатнім напрямом осі OX. Провести дотичну до графіка означає знайти число k. Нехай в точці А(x0;y0) кривої y = f (x) існує дотична. Визначимо кутовий коефіцієнт дотичної.
Для цього:
3. Знайдемо відношення:
Із трикутника АМК маємо: Так як 4. Якщо ∆x → 0, то ∆y → 0 і точка М буде переміщуватися по кривій, наближаючись до точки А. Граничним положенням січної АМ при ∆x → 0 буде дотична АТ, яка утворює з додатним напрямом осі ОX деякий кут, величину якого позначимо через ά. Отже, коефіцієнт дотичної. Поняття похідної. Ці дві задачі розв’язуються одним і тим же самим способом, який складається з таких етапів: 1. Незалежній змінній x надаємо приросту ∆x. 2. Знаходимо приріст залежної змінної - ∆y.
О3 Похідною функції y=f (x) в точці x0 називається границя відношення приросту функції до приросту аргументу при умові, що приріст аргументу прямує до нуля, а границя існує, тобто:
Функцію, яка має скінчену похідну в точці x, називають диференційованою в цій точці. Обчислення похідної називають диференціюванням. Позначення похідної: y '(x), f '(x) (за Лагранжем) або З означення похідної випливає, що похідна y '(x), в точці x є числом. Але якщо таке число існує для кожної внутрішньої точки проміжку (a, b), то похідну можна розглядати як функцію точки x з даного проміжку. Якщо Порівнюючи одержані результати першої і другої задач із означенням похідної, можна зробити висновок: якщо матеріальна точка рухається прямолінійно і її координата змінюється по закону s = s(t), то швидкість її руху v (t) в момент часу t дорівнює похідній s '(t): V(t) = S'(t) - механічний зміст похідної. Приклад 1. Точка рухається прямолінійно по закону s(t) = 5t2 + t + 3 (s — шлях в метрах, t – час в секундах). Знайдіть швидкість точки: а) в довільний момент t0; б) в момент часу t = 2 с. Розв'язання а) 1) нехай значення аргументу t0 одержало приріст Δ t, тоді t1 = t0 + Δ t. 2) Знайдемо відповідний приріст шляху Δ s = s(t0 + Δ t) - s(t0) = 5(t0 + Δ t)2 + (t0 + Δ t) + 3 – (5 t0 2 + t0 + 3) = 5 t0 2 +10 t0 Δ t + 5Δ t 2 + t0 + Δ t + 3 – 5 t0 2 – t0 – 3 = 10 t0 Δ t + 5Δ t 2 + Δ t. 3) Знайдемо відношення приросту шляху до приросту часу (середню швидкість):
4) Знайдемо границю відношення приросту шляху до приросту часу (середньої швидкості):
Отже, миттєва швидкість точки в довільний момент часу t0 дорівнює 10 t0 + 1. Отже, при заданому законі руху s(t) миттєва швидкість v(t) в довільний момент часу t обчислюється по формулі v (t) = 10 t + 1. б) Якщо t = - 2 с, то маємо v (2) = 10 · 2 +1 = 21 Відповідь: а) 10 t + 1; б)21 Геометричний зміст похідної: значення похідної функції y=f (x) в точці x0 дорівнює кутовому коефіцієнту дотичної до графіка функції в точці з абсцисою x0 : f '(x0)= k= tg ά. Фізичний зміст похідної: 1) Миттєва швидкість нерівномірного прямолінійного руху є похідна від функції, яка виражає залежність пройденого шляху 2) Сила струму є похідна від функції, яка виражає залежність кількості електрики 3) Кутова швидкість обертання тіла навколо осі є похідна від функції, яка виражає залежність кута повороту якщо 4) Лінійна густина матеріальної лінії в даній точці є похідна від функції, яка виражає залежність маси якщо 5) Теплоємність тіла при даній температурі є похідна від функції, яка виражає залежність кількості тепла якщо 6) Швидкість хімічної реакції є похідною від функції, яка виражає залежність кількості речовини якщо Таблиця похідних: - Похідні степеневих функцій. для всіх цілих n виконується рівність: (xn)' = nxn – 1. 1. Знайдіть похідні функції: а) у = х 6; б) у = х 8; в) y = x 2· x 5; г) y = Розв’язання: а) у ' = (х 6)' = 6 х 6-1 = 6 х 5; б) у ' = (х 8)' = 8 х 8-1 = 8 х 7; в) у ' = (x 2· x 5)' =(х 2+5)' =(х 7)' = 7 х 7-1 = 7 х 6; г) у ' = 2. Знайдіть похідні функцій: а) у = х -10; б) y = x 2· x - 5; в) y = Розв’язання: а) у ' =(х -10)' = -10 х -10-1 = –10 х -11; б) у ' =(x 2· x -5)' = (x 2-5)' =(х -3)' = -3 х -3-1 = -3 х -4; в) у ' = г) у ' = 3. Знайдіть похідні функції: а)
Розв'язання
- Похідні показникових та логарифмічних функцій. (еx)’ = еx. Знайдемо похідну функції f(x) = ax, скориставшись основною логарифмічною тотожністю та правилом знаходження похідної складеної функції:
Похідна показникової функції дорівнює добутку цієї функції на натуральний логарифм її основи. Приклад 1. Знайдіть похідні функцій: а) у = 5 х; б) у = е3 - 2х; в) у = (0,3sin x ); г) у = Розв'язання а) у' = (5х)' = 5хln 5; б) у' = (е3 – 2 x )' = e3 – 2 x · (3 - 2х)' = -2e3 – 2 x ; в) y' = ((0,3)sin x ) ' = (0,3)sin x ln 0,3 · (sin x)' = (0,3)sin x ln 0,3 · cos x = = ln 0,3cos x (0,3)sin x ;
г) у = (
Приклад 1. Знайдіть похідну функцій: а) у = log2x; б) у = ln (х2 + 1); в) y = lg (3x); г) у = ln2 (5х + 1). Розв'язання а) y’ = (log2x)’ = б) y’ = (ln(x2+1))’ = в) y’ = (lg(3x))’ = г) y’ = (ln2(5x+1))’ = 2ln(5x+1)·(ln(5x+1))’ = 2ln(5x+1)· = 2ln(5x+1)·
- Похідні тригонометричних функцій.
Приклад Розв’язання 1) y ' = ((l + sin x)2)' = 2(l + sin x)·(l + sin. x)' = = 2 (1 + sin x) · cos x; 2) у’ = ( 3) у' = (ctg3 x)’ = 3ctg2 x · (ctg x)' = 3ctg2 x · 4) y’ = - Похідні обернених тригонометричних функцій.
Таблиця похідних (формули диференціювання основних елементарних функцій)
Розв'язання Виконання вправ 1. Задайте формулами елементарні функції f і g, із яких побудована складена функція у = f(g(x)): а) у = cos (2 х + 3); б) у = (2x + 3)7; в) у = Відповіді: а) u = g(х) = 2х + 3; y = f(u) = cos u; б) и = g(x) =2х+3; у = f(u) = u7; в) u = g(x) =х2 +2х; у = f(и) = У складеній функції у = f(g(x)) присутня проміжна змінна u =g(x). Тому при знаходженні похідної складеної функції ми будемо вказувати, по якій змінній взято похідну, використовуючи при цьому спеціальні позначення:
Приклад 1. Знайдіть похідну функції у = (3 x 3 – 1)5. Розв'язання у = (3х3 – 1)5 — складена функція у = u5, де u = 3x3 – 1, тоді При обчисленні похідної складеної функції явне введення допоміжної букви u для позначення проміжного аргументу не є обов'язковим. Тому похідну даної функції знаходять відразу як добуток похідної степеневої функції u5 на похідну від функції 3 х 3 – 1: у' = ((3 x 3 – 1)5)' = 5(3х3 -1)4 · (3 x 3 – 1)' = 5 · (3 x 3 – 1)4 · 9 x = 45 x (3 x 3 – 1)4. Приклад 2. Знайдіть похідні функцій: а) у = Розв'язання
б) у' = (sin(3x + 5))' = cos (3х + 5) · (3x· + 5)' = 3 cos(3x + 5);
в) у = (cos2 x)' = 2 cos x · (cos x)' = 2 cos x · (- sin x) = = -2 cos x sin x = - sin 2x; г) y’ = (cos x2)' = - sin x2 · (x2)' = -2x sin x2. Тоді
де а Помноживши обидві частини (2) на Ах, дістанемо:
Перший з доданків лінійний відносно
Другий доданок - нескінченно мала вищого порядку, ніж Цей доданок не є лінійним відносно Тоді доданок f'(x)· Диференціал функції визначається добутком похідної на приріст незалежної змінної і позначається dy або df(x). Отже, маємо dy = f'(x) · Диференціалом dy називають також диференціал першого порядку. З виразу (4) бачимо що диференціал функції є функція двох незалежних змінних х і На цій підставі для будь-якої диференційованої функції y = f (x) можемо формулу (4) записати так: dy = f' (x) dx (5) Останній вираз називатимемо канонічним виразом диференціала функції y = f (x). З (5) діленням на dх (dх
Виходить, що похідну можна розглядати як відношення двох диференціалів. Тепер у позначенні похідної Вираз (3) можемо записати ще так:
Звідки
де Зауважимо, що коли в точці х0 похідна Геометричний зміст диференціалу зрозумілий з рисунка.
PN =
Отже, маємо функції f (x) при заданих значеннях x0 і ординати кривої. Таким чином, заміна приросту функції на її Рис. 1 диференціал геометричне означає заміну ординати АР кривої ординатою дотичної AQ. Зрозуміло, що така заміна доцільна для достатньо малих значень Ітак, сформулюємо геометричний зміст диференціалу: Диференціал функції дорівнює приросту ординати дотичної до графіка даної функції, коли аргумент отримує приріст Формули диференціювання. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. Правила диференціювання: I. II. III. IV. Ці правила легко одержати із відповідних правил для похідних. Доведемо, наприклад, два останніх:
Розв'язання 1. Область визначення даної функції — R. 2. Знайдемо f`(x): f`(x) = (x3 - 3x)' =3х2- 3. Похідна існує для всіх x є R. 3. Знайдемо стаціонарні (критичні) точки: f(x) = 0, 3 х2 - 3 = 0, х2 — 1 = 0, x = ±1. 4. f`(-2) = 3 · (-2)2 - 3 = 9 > 0; f`(0) = 3 · (0)2 - 3 = -3 < 0; f`(2) = 3 · (2)2 - 3 = 9 > 0. 5. Точка х = -1 є точкою максимуму, бо похідна при переході через цю точку змінює знак з «+» на «-»: хmax = -1. Точка х = 1 — є точкою мінімуму, бо похідна при переході через цю точку змінює знак з «-» на «+»: хmin = 1. Відповідь: хmax= -1, хmin= 1.
Розв'язання
f`(x)= (x4 – 4х3) = 4 x 3 – 12 х2 = 4 x 2(х – 3).
4. Наносимо стаціонарні точки на координатну пряму (рис. 49) та визначаємо знак похідної на кожному інтервалі. 5. x = 3 — точка мінімуму, бо при переході через цю точку похідна змінює знак з «–» на «+»: хmin = 3. Точка x = 0 не є точкою екстремуму, бо похідна не змінює знак при переході через цю точку. Отже, уmin = f (3) = 34 – 4 · 33 = – 27. Відповідь: уmin = f (3) = – 27. Розв'язання 1. D(f)= R. 2. Знайдемо абсциси точок перетину графіка з віссю ОХ: x3 - 3х2 = 0; х2 (х - 3) = 0; х = 0 або х = 3. Знайдемо ординату точки перетину графіка з віссю ΟΥ: у = 03 - 3 · 02 = 0. 3. Оскільки f(-x) = (-x)3 - 3(- х)2 = -x3 - 3х2, то функція не є парною, не є непарною. Функція неперіодична. 4. Знайдемо похідну f'(x) = 3 х 2 – 6 х = 3 х (х - 2). D(f’) = R. Знайдемо
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 621; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.125.7 (0.284 с.) |
 Побудуємо графік функції
Побудуємо графік функції і розглянемо поведінку цієї функції при х, близьких до 1.
і розглянемо поведінку цієї функції при х, близьких до 1. визначена при х
визначена при х  (-
(- 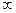 ; 1)
; 1)  (1; +
(1; +  не визначена в точці х = 1.
не визначена в точці х = 1. Отже,
Отже, 
 (рис. 11) і розглянемо поведінку функції при х, що наближається до 1.
(рис. 11) і розглянемо поведінку функції при х, що наближається до 1. f(x) = b або f(x) → b при х → а.
f(x) = b або f(x) → b при х → а. або |2х + 1 – 3| < ε; |2х – 2| < ε, 2|х – 1| < ε; |х – 1| <
або |2х + 1 – 3| < ε; |2х – 2| < ε, 2|х – 1| < ε; |х – 1| <  .
. .
. .
. Отже, якщо взяти δ =
Отже, якщо взяти δ = 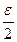 , то виконання нерівності
, то виконання нерівності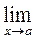 С = С, де С — постійна.
С = С, де С — постійна. ,
,  .
. .
.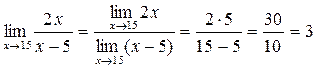 .
. .
.

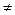 0, то маємо
0, то маємо .
.
 .
. .
. .
.
 ;
;  .
. ;
; ;
;










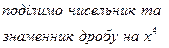 =
=
 =
=




 0 М0 М1
0 М0 М1


 .
. .
. .
. 

 tg
tg 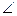 МАК.
МАК. – кутовий
– кутовий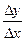 .
.  .
. .
.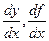 (за Лейбніцем).
(за Лейбніцем). , тоді функція f(x) має в точці x нескінченну похідну.
, тоді функція f(x) має в точці x нескінченну похідну.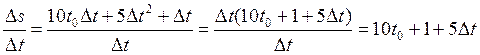

 ;
; .
. від часу
від часу  :
: 
 , яка протікає за час
, яка протікає за час  , то
, то  .
. тіла відносно осі від часу
тіла відносно осі від часу  , то
, то 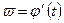 .
. від довжини цієї лінії:
від довжини цієї лінії: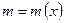 , то
, то 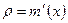
 від температури
від температури  :
: , то
, то 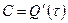 .
. , то
, то 
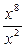 .
. = (x 8-2)' =(х 6)' = 6 х 6-1 = 6 х 5.
= (x 8-2)' =(х 6)' = 6 х 6-1 = 6 х 5. ; г) y =
; г) y = 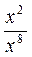 .
. = (x -6)' = -6 х -6-1 = -6 х -7;
= (x -6)' = -6 х -6-1 = -6 х -7;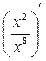 = (x 2-8)' =(х -6)' = -6 х -6-1 = -6 х -7.
= (x 2-8)' =(х -6)' = -6 х -6-1 = -6 х -7. ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.




 Отже,
Отже, .
. .
. .
.
 ;
; · (x2+1)’ =
· (x2+1)’ =  ;
; · (3x)’ =
· (3x)’ =  =
=  ;
; · (5x+1)’=
· (5x+1)’= =
=  .
.
 )’ =
)’ =  · (cos x)’ =
· (cos x)’ =  ;
; = =
= =  =
=  .
.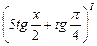 = 5
= 5 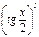 +
+ 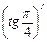 =
= 
 + 0 =
+ 0 =  .
.






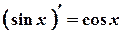






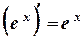



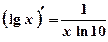



 ; г) у = sin2 x.
; г) у = sin2 x. ; г) u = g(x) = sin x; у = f(u) = u2.
; г) u = g(x) = sin x; у = f(u) = u2. — похідна функції у по аргументу x;
— похідна функції у по аргументу x; — похідна функції у по аргументу u;
— похідна функції у по аргументу u; — похідна функції u по аргументу x.
— похідна функції u по аргументу x.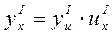 y' = (u5)' · (3х3 – 1)’ = 5u4 · 9х = 5(3х3 -1)4 · 9х = 45х(3х3 – 1)4.
y' = (u5)' · (3х3 – 1)’ = 5u4 · 9х = 5(3х3 -1)4 · 9х = 45х(3х3 – 1)4. ; б) у = sin (3х + 5); в) у = cos2x; г) y = cos x2.
; б) у = sin (3х + 5); в) у = cos2x; г) y = cos x2.
 (2)
(2) 0, якщо
0, якщо  х
х  (3)
(3)

 (6)
(6) можемо надавати dy і dx самостійного значення:
можемо надавати dy і dx самостійного значення: (7)
(7)
 Якщо
Якщо  отже, і
отже, і  0.
0. то перший доданок f формулі (3) дорівнює нулю і вже не є головною частиною приросту
то перший доданок f формулі (3) дорівнює нулю і вже не є головною частиною приросту  Маємо
Маємо
 .
.



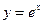



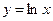







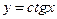





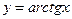






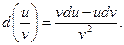


 Наносимо область визначення та стаціонарні точки на координатну пряму (рис. 48 ) і визначимо знак похідної на кожному проміжку:
Наносимо область визначення та стаціонарні точки на координатну пряму (рис. 48 ) і визначимо знак похідної на кожному проміжку: Приклад 3. Знайдіть екстремуми функції f(x) = х4 - 4х3.
Приклад 3. Знайдіть екстремуми функції f(x) = х4 - 4х3.


