
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Самостійна робота «Похідна елементарних функцій. Застосування похідної до наближених обчислень.»
1. Знайти:
2.Знайти:
Завдання для самостійної роботи А 1. Знайдіть похідні функцій:
 ; ;
б) в) г) д) е) 2. Для функції а) 3. Обчислити значення похідної функції в точці x0, якщо: а) в) Б 1. Знайдіть похідні функцій: а) б) в) г) 2. Розв’язати рівняння а) б) 3. Знайти область визначення похідної функції: а)
4. Розв’язати рівняння
В 1. Знайти точку графіка функції 2. Знайти похідну функції: а) б) 3. Розв’язати нерівність а)
ТЕМА: Зростання, спадання та екстремуми функцій. ПЛАН: 1. Ознаки зростання і спадання функції. Екстремум функції. 2. Застосування похідної до побудови графіків та їх досліджень. 3. Найбільше та найменше значення функції на проміжку. Ознаки зростання і спадання функції. Екстремум функції За допомогою похідної можна встановити проміжки зростання і спадання функції. ОЗНАКА 1. Якщо f ' (x) > 0 на проміжку, то функція f (x) зростає на цьому проміжку. ОЗНАКА 2. Якщо f ' (x) < 0 на проміжку, то функція f (x) спадає на цьому проміжку. Проміжки зростання і спадання функції часто називають проміжками монотонності цієї функції. __________________________________________________________________________________
СХЕМА №1 Знаходження проміжків зростання та спадання функції можна виконувати за таким планом: 1.Знайти область визначення заданої функції y = f (x). 2.Знайти похідну f ' (x). 3.Розв`язати нерівності (методом інтервалів): а) f ' (x) > 0, вказати проміжки зростання функції y = f (x); б) f ' (x) < 0, вказати проміжки спадання функції y = f (x). _________________________________________________________________________________
ОЗНАЧЕННЯ 1. Внутрішні точки області визначення функції, у яких похідна дорівнює нулю, або не існує називаються критичними (стаціонарними). Ці точки розбивають область визначення функції на проміжки, в яких похідна зберігає сталий знак. (Теорема Дарбу). Розглянемо функцію y = f (x), яка визначена в деякому околі точки x0 і має похідну в цій точці.
ТЕОРЕМА ФЕРМА: Якщо x0 – точка екстремуму диференційованої функції y = f (x), то f ' (x0) = 0. П`єр Ферма – французький математик (1601-1665) Теорема Ферма має наочний геометричний зміст: в точці екстремуму дотична паралельна осі абсцис, і тому її кутовий коефіцієнт f ' (x0) дорівнює нулю. Усі точки екстремуму є стаціонарними (обернене твердження невірне). Сформулюємо достатні умови того, що стаціонарна точка є точкою екстремуму (максимуму або мінімуму функції). ТЕОРЕМА. 1) Якщо функція f неперервна в точці x0, а f ' (x) > 0 на
інтервалі (а; x0) і f ' (x) < 0 на інтервалі (x0; в), то x0 – точка максимуму. ТЕОРЕМА. 1) Якщо функція f неперервна в точці x0, а f ' (x) < 0 на інтервалі (а; x0) і f ' (x) > 0 на інтервалі (x0; в), то x0 – точка мінімуму. Або: якщо похідна при переході через стаціонарну точку змінює свій знак з „+” на „ -”, то ця стаціонарна точка є точкою максимуму; якщо похідна при переході через стаціонарну точку змінює свій знак з „ -” на „+”, то ця стаціонарна точка є точкою мінімуму. СХЕМА № 2 Дослідження функції на екстремум.
2. Знайти похідну f ' (x). 3. Знайти критичні точки. 4. Відмітити критичні точки на координатній прямій, визначити знак похідної і дослідити характер поведінки функції на кожному з інтервалів, на якій робимо область визначення. 5. Визначити відносно кожної критичної точки, чи є вона точкою максимуму, мінімуму або не є точкою екстремуму взагалі.
Приклад 1. Знайдіть проміжки монотонності функції у = х3 - 3х2.
1. Область визначення функції: D(y) = R. 2. Знаходимо похідну у' = 3х2 -6х. 3. Розв'язуємо нерівності: а) у' > 0; б) у' < 0. Розв'язуємо ці нерівності методом інтервалів, для цього знаходимо нулі похідної: 3 х2 - 6х = 0, 3х(х - 2) = 0, х = 0 або х = 2. Наносимо на координатну пряму (рис. 37) нулі похідної і визначаємо знаки похідної на кожному проміжку: y'(-1) = 3 · (-1)2 - 6 · (-1) = 3 + 6 = 9 > 0; y'(1) = 3 · І2 – 6 - 1 = -3 < 0; у'(3) = 3 · 32 – 6 · 3 = 27 - 18 = 9 > 0. а) у' > 0 в кожному із проміжків (- б) у' < 0 на проміжку (0; 2), отже, функція на цьому проміжку спадає. Відповідь: функція зростає на кожному із проміжків (- Приклад 2. Знайдіть точки екстремуму функції f(x) = х3 – 3х. Розв'язання 1. Область визначення даної функції — R. 2. Знайдемо f`(x): f`(x) = (x3 - 3x)' =3х2- 3. Похідна існує для всіх x є R. 3. Знайдемо стаціонарні (критичні) точки: f(x) = 0, 3 х2 - 3 = 0, х2 — 1 = 0, x = ±1. 4. f`(-2) = 3 · (-2)2 - 3 = 9 > 0; f`(0) = 3 · (0)2 - 3 = -3 < 0; f`(2) = 3 · (2)2 - 3 = 9 > 0. 5. Точка х = -1 є точкою максимуму, бо похідна при переході через цю точку змінює знак з «+» на «-»: хmax = -1. Точка х = 1 — є точкою мінімуму, бо похідна при переході через цю точку змінює знак з «-» на «+»: хmin = 1. Відповідь: хmax= -1, хmin= 1.
Розв'язання
f`(x)= (x4 – 4х3) = 4 x 3 – 12 х2 = 4 x 2(х – 3).
4. Наносимо стаціонарні точки на координатну пряму (рис. 49) та визначаємо знак похідної на кожному інтервалі. 5. x = 3 — точка мінімуму, бо при переході через цю точку похідна змінює знак з «–» на «+»: хmin = 3. Точка x = 0 не є точкою екстремуму, бо похідна не змінює знак при переході через цю точку. Отже, уmin = f (3) = 34 – 4 · 33 = – 27. Відповідь: уmin = f (3) = – 27.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 983; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.60.166 (0.087 с.) |






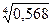



















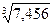






 ;
2.у = 2 x + cos x -
;
2.у = 2 x + cos x -  ;
3.у= 2 x + sin x – lnx;
4.у= x 2 - sin x +
;
3.у= 2 x + sin x – lnx;
4.у= x 2 - sin x +  ;
5.у=2 x - sin x +
;
5.у=2 x - sin x +  ;
6.y =x2 - 4x + tgx;
7.у= -
;
6.y =x2 - 4x + tgx;
7.у= -  x 3 +
x 3 +  +ctg x;
8.y = 5 x – ln x +
+ctg x;
8.y = 5 x – ln x +  ;
9.y =
;
9.y = 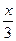 +
+  - ctgx;
10.
- ctgx;
10.  ;
11.
;
11.  ;
12.
;
12.  ;
13.
;
13. 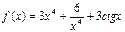 ;
14.y =3 x 3 - sin x -
;
14.y =3 x 3 - sin x -  ;
15.у = 5 x3 - cos x -
;
15.у = 5 x3 - cos x -  ;
16.у= 2 x4 - sin x +5 lnx;
17.у= 3 x 3 + 4sin x -
;
16.у= 2 x4 - sin x +5 lnx;
17.у= 3 x 3 + 4sin x - 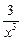 ;
18.у=5 x - 2sin x +
;
18.у=5 x - 2sin x +  ;
19.y =3x2 - 8x - 4tgx;
20.у=
;
19.y =3x2 - 8x - 4tgx;
20.у= 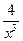 - ctg x;
21.y = 7 x3 +3 ln x -
- ctg x;
21.y = 7 x3 +3 ln x - 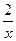 ;
22.y =
;
22.y =  -
-  + tgx;
23.
+ tgx;
23.  ;
24.
;
24.  ;
25.
;
25.  ;
26.
;
26.  ;
27.у=5 x - 2sin x +
;
27.у=5 x - 2sin x +  ∙
∙  ;
5.
;
5.  ;
6.
;
6.  ;
7.
;
7. 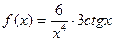 ;
8.y =cos x ∙
;
8.y =cos x ∙  ;
10.у= sin x ∙
;
10.у= sin x ∙  ∙ ctg x;
15.y = (2 x3 + 3) ∙ ln x;
16.y =
∙ ctg x;
15.y = (2 x3 + 3) ∙ ln x;
16.y =  ∙
∙ 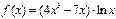 ;
18.
;
18.  ;
19.
;
19.  ;
20.
;
20.  ;
21.y =4cos x ∙
;
21.y =4cos x ∙  ;
22.у = (2 x3 +5)∙
;
22.у = (2 x3 +5)∙  ;
24.у= (2 x 2 - 5х) ∙ lnx;
25.у=(5 x3 - х)∙
;
24.у= (2 x 2 - 5х) ∙ lnx;
25.у=(5 x3 - х)∙  ;
26.у=
;
26.у=  ∙ ctg x;
27.
∙ ctg x;
27. 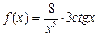 .
.
 ;
2.f(x) =
;
2.f(x) =  ;
3.f(x) =
;
3.f(x) =  ;
4.f(x) =
;
4.f(x) =  ;
5.f(x) =
;
5.f(x) =  ;
6.f(x) =
;
6.f(x) =  ;
7.f(x) =
;
7.f(x) =  ;
8.f(x) =
;
8.f(x) =  ;
9.f(x) =
;
9.f(x) = 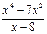 ;
10.f(x) =
;
10.f(x) =  ;
11.f(x) =
;
11.f(x) =  ;
12.f(x) =
;
12.f(x) =  ;
13.f(x) =
;
13.f(x) =  ;
14.f(x) =
;
14.f(x) =  ;
15.f(x) =
;
15.f(x) =  ;
16.f(x) =
;
16.f(x) =  ;
17.f(x) =
;
17.f(x) = 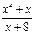 ;
18.f(x) =
;
18.f(x) =  ;
19.f(x) =
;
19.f(x) =  ;
20.f(x) =
;
20.f(x) =  ;
21.f(x) =
;
21.f(x) =  ;
22.f(x) =
;
22.f(x) =  ;
23.f(x) =
;
23.f(x) =  ;
24.f(x) =
;
24.f(x) =  ;
25.f(x) =
;
25.f(x) =  ;
26.f(x) =
;
26.f(x) =  ;
27.f(x) =
;
27.f(x) =  .
.
 ;
ж)
;
ж)  ;
з)
;
з)  ;
к)
;
к)  ;
л)
;
л)  ;
м)
;
м)  .
.
 ;
; ;
; ;
; ;
; ;
; знайти:
знайти: ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г) 
 ; д)
; д)  ;
;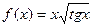 ; е)
; е)  .
. ;
; ;
; , якщо:
, якщо: ;
; .
. ; б)
; б)  .
. , якщо
, якщо  .
. , у якій не можна побудувати до нього дотичну.
, у якій не можна побудувати до нього дотичну. в)
в) 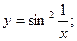 г)
г) 
 д)
д) 
 , якщо:
, якщо: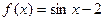 ; б)
; б)  .
. Розв'язання
Розв'язання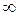 ; 0); (2; +
; 0); (2; +  Наносимо область визначення та стаціонарні точки на координатну пряму (рис. 48 ) і визначимо знак похідної на кожному проміжку:
Наносимо область визначення та стаціонарні точки на координатну пряму (рис. 48 ) і визначимо знак похідної на кожному проміжку: Приклад 3. Знайдіть екстремуми функції f(x) = х4 - 4х3.
Приклад 3. Знайдіть екстремуми функції f(x) = х4 - 4х3.


