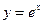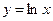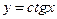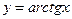Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Друга похідна, її фізичний зміст.
Дії знаходження похідних функцій називаються диференціюванням функцій і виконуються за такими правилами: - Похідна суми певної скінченої кількості функцій дорівнює сумі похідних доданків. - Похідна різниці двох функцій дорівнює різниці похідних зменшуваного і від’ємника. - Похідна добутку двох функцій дорівнює сумі добутків першої функції на похідну другої функції і другої функції на похідну першої функції. Друга похідна та її фізичний зміст. Нехай функція
Приклад 1.: Знайти другу похідну слідуючих функцій:
Розв’язання: 1) Знайдемо першу похідну: Тепер знайдемо другу похідну
2)
3)
Похідна від швидкості за часом є прискорення:
Приклад 2. Точка рухається прямолінійно за законом Розв’язання: Знайдемо прискорення даної точки. Для цього знайдемо похідну від шляху: Тепер знайдемо прискорення, для цього знайдемо другу похідну від шляху:
Величина прискорення являється постійною для довільного значення Приклад 2. Закон руху тіла знаходиться рівнянням Розв’язання: Знайдемо прискорення тіла в будь який момент часу, для цього знайдемо другу похідну від шляху:
Далі розв’яжемо рівняння
Диференціал функції, його геометричних зміст. Нехай функція y = f (x) має в даній точці похідну
Тоді
де а Помноживши обидві частини (2) на Ах, дістанемо:
Перший з доданків лінійний відносно
Другий доданок - нескінченно мала вищого порядку, ніж Цей доданок не є лінійним відносно Тоді доданок f'(x)·
Диференціал функції визначається добутком похідної на приріст незалежної змінної і позначається dy або df(x). Отже, маємо dy = f'(x) · Диференціалом dy називають також диференціал першого порядку. З виразу (4) бачимо що диференціал функції є функція двох незалежних змінних х і На цій підставі для будь-якої диференційованої функції y = f (x) можемо формулу (4) записати так: dy = f' (x) dx (5) Останній вираз називатимемо канонічним виразом диференціала функції y = f (x). З (5) діленням на dх (dх
Виходить, що похідну можна розглядати як відношення двох диференціалів. Тепер у позначенні похідної Вираз (3) можемо записати ще так:
Звідки
де Зауважимо, що коли в точці х0 похідна Геометричний зміст диференціалу зрозумілий з рисунка.
PN =
Отже, маємо функції f (x) при заданих значеннях x0 і ординати кривої. Таким чином, заміна приросту функції на її Рис. 1 диференціал геометричне означає заміну ординати АР кривої ординатою дотичної AQ. Зрозуміло, що така заміна доцільна для достатньо малих значень Ітак, сформулюємо геометричний зміст диференціалу: Диференціал функції дорівнює приросту ординати дотичної до графіка даної функції, коли аргумент отримує приріст Формули диференціювання. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. Правила диференціювання: I. II. III. IV. Ці правила легко одержати із відповідних правил для похідних. Доведемо, наприклад, два останніх:
|
||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 1845; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.165.246 (0.023 с.) |
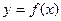 диференційована на деякому проміжку
диференційована на деякому проміжку 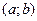 та має похідну
та має похідну 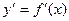 . Якщо ця функція є диференційованою в деякій точці
. Якщо ця функція є диференційованою в деякій точці 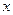 інтервалу
інтервалу 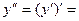
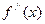
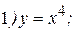
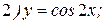

 .
.
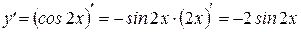 ;
;
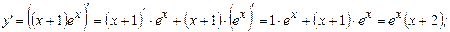

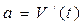

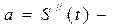 механічний (фізичний) зміст похідної другого порядку.
механічний (фізичний) зміст похідної другого порядку.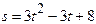 . Знайти прискорення точки в момент
. Знайти прискорення точки в момент 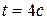 .
.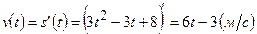 .
. .
.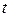 , отже рух точки за даним законом проходить із постійним прискоренням, тобто
, отже рух точки за даним законом проходить із постійним прискоренням, тобто 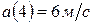 .
.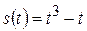 . Яке прискорення тіла в момент, коли його швидкість дорівнює 11 м/с?
. Яке прискорення тіла в момент, коли його швидкість дорівнює 11 м/с?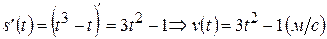
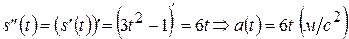
 і знайдемо потрібний нам момент часу:
і знайдемо потрібний нам момент часу:  . Тепер знайдемо прискорення тіла в момент
. Тепер знайдемо прискорення тіла в момент  :
: 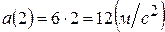 .
.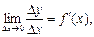 (1)
(1) (2)
(2) 0, якщо
0, якщо  х
х  (3)
(3)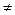 0 є нескінченно малою одного порядку з
0 є нескінченно малою одного порядку з 

 (6)
(6) можемо надавати dy і dx самостійного значення:
можемо надавати dy і dx самостійного значення: (7)
(7)
 Якщо
Якщо  отже, і
отже, і  0.
0. то перший доданок f формулі (3) дорівнює нулю і вже не є головною частиною приросту
то перший доданок f формулі (3) дорівнює нулю і вже не є головною частиною приросту  Маємо
Маємо
 .
.