
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Относительный покой жидкостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы: Визуальное наблюдение формы свободной поверхности жидкости во вращающемся сосуде; опытная проверка аналитического выражения (3.3); построение эпюр гидростатического давления для абсолютного и относительного покоя; определение сил действия жидкости на боковые стенки и дно резервуара.
Основные положения и расчетные зависимости Из уравнения гидростатики, определяющего равновесие покоящейся жидкости, запишем:
Для поверхности равного давления (dp=0) имеем
При вращении сосуда с жидкостью с постоянной скоростью вокруг вертикальной оси на каждую частицу жидкости действуют массовые силы–сила тяжести и центробежная сила инерции. Проекции ускорения массовых сил ах, ау, az на оси координат в данном случае будут (рис. 3.1):
С учетом этого выражение (3.2) примет вид
Интегрирование последнего выражения дает уравнение параболоида вращения:
где Закон распределения давления в жидкости при относительном покое имеет вид
где Рабс - абсолютное давление в любой точке жидкости с текущими координатами r и z (рис. 3.1).
Рис. 3.1. Схема установки для изучения относительного покоя жидкости во вращающемся относительно вертикальной оси цилиндре
Например: если точка А находится на дне резервуара, совпадая с началом координат, тогда r = 0, z = 0, по уравнению (3.5) имеем
Если точка В находится на дне резервуара у его боковой стенки (рис. 3.1), имеем r = R, z = 0, тогда по уравнению (3.5)
Изменение давления по вертикали такое же, как и в неподвижном сосуде.
Порядок выполнения работы Опыт проводится на специальной установке, состоящей из цилиндра 1 с прозрачными стенками из органического стекла, вставленного в обойму 2. Осевой валик 3 обоймы с помощью редуктора соединен с электродвигателем. Число оборотов электродвигателя регулируется реостатом по тахометру. Над цилиндром установлена горизонтальная линейка с передвижной мерной иглой 4. В цилиндр наливается глицерин (ρ = 1240 кг/м3) (примерно до половины цилиндра). Замеряется уровень жидкости Но и внутренний радиус сосуда R. Установка включается в сеть. Затем цилиндр приводится во вращение с постоянным числом оборотов n, которое замеряется по тахометру. Когда поверхность жидкости примет установившуюся форму, мерной иглой измеряются координаты нескольких точек на свободной поверхности (CDN, рис. 3.1).
Данные замеров и расчетов помещаются в таблицу 3.1
Таблица 3.1
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 428; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.123.56 (0.008 с.) |

 . (3.1)
. (3.1) (3.2)
(3.2)
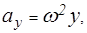
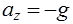
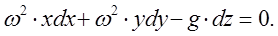 (3.3)
(3.3)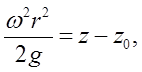 (3.4)
(3.4)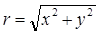 ; х, у, z - текущие координаты точек на свободной поверхности жидкости; z0 - координата пересечения параболоида с осью вращения; w - угловая скорость вращения; ρ - плотность жидкости.
; х, у, z - текущие координаты точек на свободной поверхности жидкости; z0 - координата пересечения параболоида с осью вращения; w - угловая скорость вращения; ρ - плотность жидкости.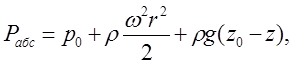 (3.5)
(3.5)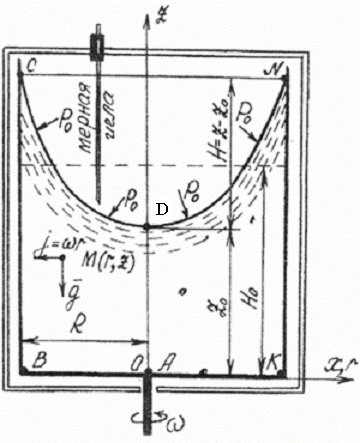
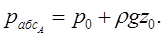 (3.6)
(3.6)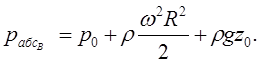 (3.7)
(3.7)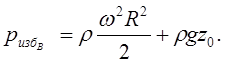 (3.7)*
(3.7)* оп
оп



