Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Одинаково распределенные взаимно независимыеСодержание книги
Поиск на нашем сайте
случайные величины. Рассмотрим n взаимно независимых случайных величин X1, X2,…, Xn, которые имеют одинаковые распределения, а следовательно, одинаковые математические ожидания и дисперсии, т.е. М(X1) = М(X2) =…= М(Xn) = μx D(X1) = D(X2) =…= D(Xn) = Обозначим среднее арифметическое случайных величин как
Теорема. Математическое ожидание, дисперсия и стандартное отклонение средней арифметической n одинаково распределенных взаимно независимых случайных величин есть
▼ Вычислим математическое ожидание и дисперсию
Пример. Дисперсия каждой из 9 одинаково распределенных взаимно независимых случайных величин равна 36. Найти дисперсию и стандартное отклонение среднего арифметического этих величин. ▼ По условию n = 9,
Математическое ожидание и дисперсия числа появления событий В n независимых испытаниях
I. Теорема. Математическое ожидание числа появления событий в одном испытании равно вероятности р этого события, а дисперсия - произведению pq, т.е. М(Х) = р, D(X) = pq. ▼ Пусть производится 1 испытание, в котором вероятность события А равно р. Случайная величина Х (число появления события А в одном испытании) может принимать только два значения: х1 = 0, (событие А не наступило) с вероятностью q = 1 – p, и х2 = 1, (событие А наступило) с вероятностью p, Запишем закон распределения Х в виде таблицы M(X) = 0∙q + 1∙p = p, μ = p; M(X2) = 02∙q + 12∙p = p, D(X) = M(X2) - μ2 = p – p2 = p(1 – p) = pq. II. Теорема. Математическое ожидание и дисперсия числа появления события А в n независимых испытаниях, в каждом из которых вероятность появления события А постоянна и равна p есть M(X) = np, D(X) = npq. ▼ Случайная величина Х (общее число появлений события А в n испытаниях) равна сумме появлений события в отдельных испытаниях: Х = X1+ X2 +…+ Xn. Величины X1, X2,…, Xn взаимно независимые и имеют одинаковые распределения, т.е. М(X1) = М(X2) =…= М(Xn) = p D(X1) = D(X2) =…= D(Xn) = pq, тогда М(Х) = М(X1) + М(X2) +…+ М(Xn) = np, D(Х) = D(X1) + D(X2) +…+ D(Xn) = npq, Пример. Производится 10 независимых испытаний, в каждом из которых вероятность появления события равна 0,6. Найти математическое ожидание и дисперсию случайной величины Х (число появлений события в этих испытаниях). ▼ n = 10. p = 0,6; q = 0,4. M(X) = np = 10∙0,6 = 6, т.е. в 10 испытаниях событие появится в среднем в 6 случаях, D(X) = npq = 10∙0,6∙0,4 = 2,4. Следствие. Математическое ожидание и дисперсия частости m/n появления события А в n независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна
▼ Случайная величина Х = m – общее число появления события А в n независимых испытаниях. Вычислим математическое ожидание и дисперсию частости:
Пример. Вероятность выигрыша по облигации за все время его действия равна 0,1. Найти математическое ожидание, дисперсию и стандартное отклонение доли (частости) выигравших облигаций среди 19 приобретенных. ▼ n = 19. p = 0,1; q = 0,9.
Основные законы распределения ДСВ.
Биномиальное распределение. Дискретная случайная величина Х, которая принимает значение m с вероятностью Теорема. Математическое ожидание и дисперсия случайной величины Х, распределенной по биномиальному закону, есть: M(X) = np, D(X) = npq. Пример. Вероятность попадания стрелком в мишень равна 0,8. Записать закон распределения случайной величины Х (числа попаданий в мишень), если стрелок сделал 20 выстрелов. Найти М(Х), D(X). ▼ n = 20. p = 0,8; q = 0,2. P(X = m) = М(Х) = np= 20∙0,8 = 16 – среднее число попаданий в мишень при 20 выстрелах, D(X) = npq = 20∙0,8∙0,2 = 3,2.
Закон распределения Пуассона. Дискретная случайная величина Х, которая принимает значение m с вероятностью Теорема. Математическое ожидание и дисперсия случайной величины Х, распределенной по закону Пуассона, совпадают и равны параметру λ этого закона, т.е. M(X) = λ, D(X) = λ. Пример. Случайная величина Х распределена по закону Пуассона с параметром λ =2. Найти вероятности Р(Х = 0), Р(Х > 0). ▼ m = 0, P(X = 0) = e 1 – 0,1353 = 0,8675.
Геометрическое распределение. Пусть производятся независимые испытания, в каждом из которых вероятность появления события А равна р, и, следовательно, вероятность его непоявления q = 1 – p. Испытания заканчиваются, как только появится событие А. Таким образом, если событие А появилось в m – ом испытании, то в предшествующих m – 1 испытаниях оно не появилось. Пусть в первые m – 1 испытаниях событие А не наступило, а в m – ом испытании появилось, т.е.
Вероятность такой цепочки по теореме умножения вероятности независимых событий есть Дискретная случайная величина Х, которая принимает значение m с вероятностью
называется геометрическим распределением с параметром р. Теорема. Математическое ожидание и дисперсия случайной величины Х, имеющей геометрическое распределение с параметром р, равна M(X) = 1/p, D(X) = q/p2, где q = 1 – p. Пример. Из большой партии изделий контроль качества проводится до 1 – го появления бракованного изделия. В результате проверок обнаружилось, что бракованное изделие впервые появляется в среднем при десятом испытании.. Определить вероятность р брака изделия. ▼ Случайная величина Х – число испытаний до 1 – го появления бракованного изделия. По условию, среднее значение М(Х) = 10. Из выражения M(X) = 1/p = 10 следует, что р = 1/10 = 0,1.
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 429; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.008 с.) |

 .
.

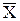
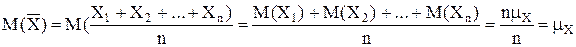


 = 36, тогда
= 36, тогда  .
.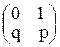 , тогда
, тогда .
. ,
,  .
. .
.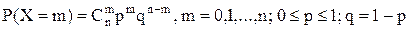 , называется распределенной по биномиальному закону с параметрами n, p.
, называется распределенной по биномиальному закону с параметрами n, p. - закон распределения Х,
- закон распределения Х, , называется распределенной по закону Пуассона с параметром λ
, называется распределенной по закону Пуассона с параметром λ