
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые характеристики ДСВ.
Пусть ДСВ Х задана таблицей распределения. Математическим ожиданием ДСВ Х называется сумма произведений всех ее возможных значений на соответствующие им вероятности, т.е. M(X) = x1p1+ x2p2 +… = ∑xipi, где суммирование производится по всем возможным значениям случайной величины. Пример. Найти М(Х) случайной величины Х, заданной таблицей
▼ М(Х) = 2∙0,3 + 3∙0,1 + 5∙0,6 = 3,9. Математическое ожидание случайной величины – это среднее ее значение и обозначается М(Х) = μХ. Замечание. Если ясно, о какой случайной величине идет речь, то нижний индекс в μХ можно не указывать и записывать как μ. Геометрически – математическое ожидание случайной величины – это центр распределения. Математическое ожидание случайной величины является величиной неслучайной, постоянной. Математическое ожидание функции g(X) определяется: M(g(X)) = ∑g(xi)pi, где суммирование производится по все возможным значениям Х. В частности, если g(X) =Х2, то M(Х2) = ∑
Свойства математического ожидания. Пусть a, b – const, а Х, У – случайные величины, тогда 1. M(a) = a; 2. M(bX) = bM(X); 3. M(X + Y) = M(X) + M(Y); 4. M(XY) = M(X)M(Y), если Х, У независимы; 5. M(X – μ) = 0. Пример. Найти M(Z), где Z = 8X – 5Y + 7, если M(X) =3. M(Y) = 2. ▼ M(Z) = M(8X – 5Y + 7) = 8M(X) – 5M(Y) + 7 = 8∙3 - 5∙2 + 7 = 21.
Дисперсия ДСВ. Пусть Х – случайная величина, а μ = М(Х). Дисперсией случайной величины Х называется математическое ожидание квадрата отклонения случайной величины Х относительно математического ожидания, т.е. D(X) = M(X – μ)2, где μ = М(Х). Для вычисления дисперсии часто используется другое выражение, получаемое из определения дисперсии: D(X) = M(X2) – μ2. ▼ D(X) = M(X – μ)2 = M(X2 - 2μX + μ2) = M(Х2) -2μМ(Х) + μ2 = M(Х2) - 2μ2 + μ2 = M(X)2 – μ2. Дисперсия ДСВ Х определяется выражением: D(X) = ∑(xi – μ)2pi, или D(X) = ∑ Пример. Найти D(X) случайной величины Х, заданной таблицей
▼ М(Х) = 2∙0,3 + 3∙0,1 + 5∙0,6 = 3,9, μ = 3,9. Дисперсию можно вычислить двумя способами: 1) D(X) = ∑(xi – μ)2pi= (2 – 3,9)2∙0,3 + (3 – 3,9)2∙0,1+ (5 – 3,9)2∙0,6 =1,89. 2) M(X)2 = ∑ D(X) = ∑ Дисперсия является мерой рассеяния случайной величины относительно средней (центра). Размерность дисперсии не совпадает с размерностью случайной величины.
Стандартным отклонением (средним квадратическим отклонением) случайной величины Х называется корень квадратный из ее дисперсии, т.е.
Стандартное отклонение показывает, насколько в среднем отклоняется случайная величина Х относительно средней. Дисперсия (стандартное отклонение) случайной величины Х является величиной неслучайной, постоянной.
Свойства дисперсии. Пусть a, b – const, а Х, У – случайные величины, тогда 1. D(a) = a; 2. D(bX) = b2D(X); 3. D(X ± Y) = D(X) + D(Y), если Х, У независимы. Докажем свойство 3. ▼ D(X ± Y) = M[(X ± Y) – (μx ± μy)] 2 = M[(X - μx) ± (Y - μy)] 2 = M[(X - μx)2 + (Y - μy) 2 ± 2(X - μx) (Y - μy)] = D(X) + D(Y) ± 2M[(X - μx) (Y - μy)]. Если Х, У – независимы, то M[(X - μx) (Y - μy)] = 0, следовательно, D(X ± Y) = D(X) + D(Y). Пример. Найти D(Z), где Z = 8X – 5Y + 7, если известно, что случайные величины Х, У независимы и D(X) = 1,5; D(Y) = 1. ▼ D(Z) = D(8X – 5Y + 7) = 64D(X) + 25D(Y) = 64∙1,5 + 25∙1 = 121.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 243; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.172.146 (0.007 с.) |
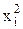 pi. Например, для рассматриваемого примера M(Х2) = 22∙0,3 + 32∙0,1 + 52∙0,6 = 17,7.
pi. Например, для рассматриваемого примера M(Х2) = 22∙0,3 + 32∙0,1 + 52∙0,6 = 17,7.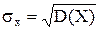 .
.


