
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Для обучающихся по проведениюСодержание книги
Поиск на нашем сайте
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ОБУЧАЮЩИХСЯ ПО ПРОВЕДЕНИЮ ПРАКТИЧЕСКИХ ЗАНЯТИЙ для специальности 210414 «Техническое обслуживание и ремонт радиоэлектронной техники (по отраслям)» 140448 «Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (по отраслям)»
Учебная дисциплина «МАТЕМАТИКА»
Смоленск Г.
Рассмотрено и одобрено ЦМК общеобразовательных дисциплин Предс. ЦМК ____________ /Воронова Ю.А./ Протокол №______ «___»___________20__г.
Составитель: Полякова Л.П., преподаватель ОГБОУ СПО «Смоленский политехнический колледж»
Рецензент: Елисеев Ю. Г., директор ОГБОУ СПО «Смоленский политехнический колледж»
Методические указания для обучающихся по проведению практических занятий являются частью основной профессиональной образовательной программы ОГБОУ СПО «Смоленский политехнический колледж» по специальностям 210414 «Техническое обслуживание и ремонт радиоэлектронной техники (по отраслям)» в соответствии с требованиями федеральных государственных образовательных стандартах третьего поколения (далее – ФГОС). Методические указания для обучающихся по проведению практических занятий включают в себя предисловие, цели работы, пояснения к работе, задание, порядок иобразец отчёта, контрольные вопросы, литературу, приложения.
СОДЕРЖАНИЕ
ПРЕДИСЛОВИЕ
УВАЖАЕМЫЕ СТУДЕНТЫ! Методические указания для обучающихся по проведению практических занятий по учебной дисциплине «Математика» созданы вам в помощь для работы на занятиях, правильного составления отчётов. Приступая к выполнению задания, вы должны внимательно прочитать цели, ознакомиться с пояснениями к работе, содержащими краткие теоретические сведения по теме работы и методические рекомендации, ответить на контрольные вопросы. Практическое занятие содержит задание, состоящее из шести вариантов, включающих задачи, соответствующиеуказаннымв ФГОСтребованиям к уровню вашей подготовки. Выполнять задание, делать выводы по проделанной работе вы должны согласно инструкции преподавателя. Отчёт о работе вы должны оформить по приведённому образцу. Наличие положительных оценок по практическим занятиям необходимо для допуска к экзамену по учебной дисциплине «Математика.». В случае отсутствия на учебном занятии по любой причине или получения неудовлетворительной оценки за практическое занятиевы должны выполнить работу или пересдать. ВНИМАНИЕ! В результате выполнения заданий практических занятий по УД «Математика» вы освоите умения
- решать прикладные задачи в области профессиональной деятельности, на основе знаний: – значения математики в профессиональной деятельности и при освоении профессиональной образовательной программы; - основных математических методов решения прикладных задач в области профессиональной деятельности; - основных понятий и методов математического анализа, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики; - основ интегрального и дифференциального исчисления. Желаем вам успехов! Практическое занятие № 1 Действия над комплексными числами вразличных формах Цели: в результате выполнения практической работы, обучающиеся должны уметь выполнять действия над комплексными числами в алгебраической, тригонометрической и показательной формах, уметь переходить от алгебраической формы комплексного числа к тригонометрической, показательной и обратно.
Пояснения к работе Комплексными числами называют числа вида a + bi, где a и b – действительные числа, а число i, определяемое равенством Модулем комплексного числа Угол φ между положительным направлением оси Ох и вектором Введение мнимой единицы позволило вычислять корень квадратный из отрицательного числа. Так Рассмотрим решение квадратное уравнение Запись комплексного числа z = a + bi называют алгебраической формой записи комплексного числа. Тригонометрическая форма записи комплексного числа: Для представления комплексного числа в тригонометрической или показательной форме надо: 1) найти модуль этого числа
Представить в тригонометрической и показательной форме числа: 1) Для того, чтобы сложить или вычесть комплексные числа надо раскрыть скобки и привести подобные,например: (-2+3 i) + (5+2 i) = (-2+5)+(3+2) i = 3+5 i. 2. (-2+3 i) - (5+2 i) = (-2-5)+(3-2) i = -7+ i. Можно произвести умножение по правилу умножения многочленов, учесть, что Деление можно выполнить умножив числитель и знаменатель на число сопряженное знаменателю, например: Произведение сопряженных комплексных чисел – число действительное и неотрицательное, равное сумме квадратов действительной и мнимой части числа
Умножение, деление, возведение в степень, извлечение корня удобно выполнять в тригонометрической или показательной формах.
Задание Вариант 1 Задача 1. Найдите корни уравнения и изобразите их на комплексной плоскости: Задача 2.Выполните действия над комплексными числами: а) Вариант 2 Задача 1. Найдите корни уравнения и изобразите их на комплексной плоскости: Задача 2.Выполните действия над комплексными числами: а) Вариант 3 Задача 1. Найдите корни уравнения и изобразите их на комплексной плоскости: Задача 2.Выполните действия над комплексными числами, в пункте в ответ запишите в алгебраической, тригонометрической и показательной формах: а) Вариант 4 Задача 1. Найдите корни уравнения и изобразите их на комплексной плоскости: Задача 2.Выполните действия над комплексными числами, в пункте в ответ запишите в алгебраической, тригонометрической и показательной формах: а) Вариант 5 Задача 1. Найдите корни уравнения и изобразите их на комплексной плоскости: Задача 2.Выполните действия над комплексными числами, в пункте в ответ запишите в алгебраической, тригонометрической и показательной формах: а) Вариант 6 Задача 1. Найдите корни уравнения и изобразите их на комплексной плоскости: Задача 2.Выполните действия над комплексными числами, в пункте в ответ запишите в алгебраической, тригонометрической и показательной формах: а) Содержание отчёта Отчёт о проделанной работе должен содержать: - название темы практического занятия; - цели практического занятия; - условие задачи; - подробное решение задачи; - ответ. Контрольные вопросы 1. Могут ли числа, 2. Как умножают, делят, возводят в степень, извлекают корни из комплексных чисел, записанных в алгебраической, тригонометрической и показательной формах? 3. Какими формулами пользуются для перехода от одной формы комплексного числа к другой? 4. Укажите на комплексной плоскости точки, соответствующие числам
Литература: 1. Богомолов Н.В. Практические занятия по математике. – М.: «Высшая школа» 2002. с. 229 – 242 2. Валуцэ И.И., Дилигул Г.Д. Математика для техникумов. – М.: «Наука» 1995. с. 78-117
Практическое занятие № 2 Пояснения к работе Пусть функция Если предел функции Аналогично, Функцию Функцию называют бесконечно малой при Если функция ƒ(x) – бесконечно малая, то функция Теоремы о пределах. Теорема 1. Пусть
Теорема 2. Предел многочлена Вычислить пределы: 1. 2. 3. Замечательные пределы позволяют раскрыть неопределенности Первый замечательный предел: Второй замечательный предел: Вычислить пределы функций: 1. 2.
3. 4.
Здесь использовали свойство предела. «Пусть дана функция ƒ(φ(х)), причем функция ƒ - непрерывная на множестве значений функции у = φ(х), тогда Задание. Вариант 1. Задача 1. Найдите пределы функций: а) Задача 2. Примените замечательные пределы для нахождения пределов функций: а) б) Вариант 2. Задача 1. Найдите пределы функций: а) Задача 2. Примените замечательные пределы для нахождения пределов функций: а) Вариант 3. Задача 1. Найдите пределы функций: а) Задача 2. Примените замечательные пределы для нахождения пределов функций: а) Вариант 4. Задача 1. Найдите пределы функций: а) Задача 2. Примените замечательные пределы для нахождения пределов функций: а) Вариант 5. Задача 1. Найдите пределы функций: а) Задача 2. Примените замечательные пределы для нахождения пределов функций: а) Вариант 6. Задача 1. Найдите пределы функций: а) Задача 2. Примените замечательные пределы для нахождения пределов функций: а) Содержание отчёта Отчёт о проделанной работе должен содержать: - название темы практического занятия; - цели практического занятия; - условие задачи; - подробное решение задачи; - ответ. Контрольные вопросы 1. Какая существует связь между бесконечно большой и бесконечно малой функциями?
2. Как раскрывают неопределенности 3. Какими теоремами о пределах вы пользовались при вычислении пределов? 4. Какие неопределенности помогают раскрыть замечательные пределы?
Литература: 1. Богомолов Н.В. Практические занятия по математике. – М.: «Высшая школа» 2002. с. 75 – 83. 2. Омельченко В.П., Курбатова Э.В. Математика. - Ростов-на-Дону: «Феникс» 2011.- с. 73 – 85. Практическое занятие № 3 Пояснения к работе Производной функции Функция Основные правила дифференцирования: Пусть U=U(x) и V=V(x) – функции, имеющие производные.
Формулы дифференцирования: 1. Производная сложной функции: Пример 1. Найти производные функций: 1) Решение. 1) 2) 3) 4) 5) 6) Задание Вариант 1 Задача 1. Найдите производные функций: а) Задача 2. Вычислите значение производных заданных функций в указанных точках: а) Вариант 2 Задача 1. Найдите производные функций: а) Задача 2. Вычислите значение производных заданных функций в указанных точках: а) Вариант 3 Задача 1. Найдите производные функций: а) Задача 2. Вычислите значение производных заданных функций в указанных точках: а) Вариант 4 Задача 1. Найдите производные функций: а) Задача 2. Вычислите значение производных заданных функций в указанных точках: а) Вариант 5 Задача 1. Найдите производные функций: а) Задача 2. Вычислите значение производных заданных функций в указанных точках: а) Вариант 6 Задача 1. Найдите производные функций: а) Задача 2. Вычислите значение производных заданных функций в указанных точках: а) Содержание отчёта Отчёт о проделанной работе должен содержать: - название темы практического занятия; - цели практического занятия; - условие задачи; - подробное решение задачи; - ответ. Контрольные вопросы 1. Как вычисляют производную сложной функции? 2. Какими правилами дифференцирования вы пользовались при нахождении производных функций? 3. Какими формулами дифференцирования вы пользовались при нахождении производных функций? 4. Как называют операцию нахождения производной функции?
Литература: 1. Богомолов Н.В. Практические занятия по математике. – М.: «Высшая школа» 2002. с. 94 – 100. 2. Омельченко В.П., Курбатова Э.В. Математика. - Ростов-на-Дону: «Феникс» 2011.- с. 98 – 104. Практическое занятие № 4 Решение прикладных задач Цели: в результате выполнения практической работы, обучающиеся должны уметь применять знания физического смысла производной к решению практических задач и исследовать функции на монотонность, экстремумы. Пояснения к работе Задание Вариант 1 Задача 1. Изменение силы тока Задача 2. Исследовать функцию Вариант 2 Задача 1. Изменение силы тока Задача 2. Исследовать функцию Вариант 3 Задача 1. Закон изменения температуры Т в зависимости от времени задан уравнением Задача 2. Исследовать функцию Вариант 4 Задача 1. Закон изменения температуры Т в зависимости от времени задан уравнением Задача 2. Исследовать функцию Вариант 5 Задача 1. Тело массой 10 кг движется прямолинейно по закону Задача 2. К источнику постоянного тока с электродвижущейся силой Е и внутренним сопротивлением Вариант 6 Задача 1. Тело массой 100 кг движется прямолинейно по закону Задача 2. Из N одинаковых элементов можно различными способами составить батарею, соединяя n элементов последовательно, а затем полученные группы (числом |

 , называется мнимой единицей; а называют действительной частью комплексного числа, b – его мнимой частью.
, называется мнимой единицей; а называют действительной частью комплексного числа, b – его мнимой частью. называют число
называют число  . Модуль комплексного числа – неотрицательное действительное число, причем
. Модуль комплексного числа – неотрицательное действительное число, причем  тогда и только тогда, когда
тогда и только тогда, когда  .
. , называют аргументом комплексного числа
, называют аргументом комплексного числа  . Для числа
. Для числа  аргумент не определен.
аргумент не определен.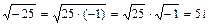 , так как
, так как  . Значит можно решить квадратное уравнение, которое имеет отрицательный дискриминант.
. Значит можно решить квадратное уравнение, которое имеет отрицательный дискриминант. ,
,  ,
,  ,
,  . Ответ:
. Ответ:  .
. , п оказательная форма записи комплексного числа:
, п оказательная форма записи комплексного числа:  , аналогично,
, аналогично, 
 ,
, 

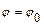
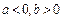


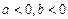
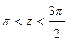



 или
или 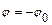


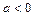 ,
, 




 . Решение:
. Решение:  ,
, 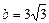 . Значит,
. Значит, 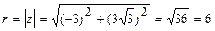 . Найдем
. Найдем  . Поскольку
. Поскольку  и
и  . Поэтому,
. Поэтому,  – тригонометрическаяформа комплексного числа,
– тригонометрическаяформа комплексного числа,  – показательная форма комплексного числа.
– показательная форма комплексного числа. .
. .
. .
.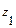 и
и 
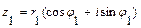



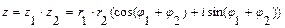
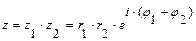



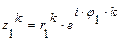
 ,
где k = 0,1,…, n -1
,
где k = 0,1,…, n -1
 ,
где k = 0,1,…, n -1
,
где k = 0,1,…, n -1
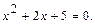
 ; б)
; б)  ; в)
; в)  .
.
 ; б)
; б)  ; в)
; в)  .
.
 ; б)
; б) 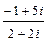 ; в)
; в)  ; г)
; г) 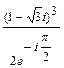 .
.
 ; б)
; б) 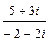 ; в)
; в)  ; г)
; г)  .
.
 ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  .
.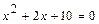
 ; б)
; б)  ; в)
; в)  ; г)
; г) 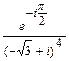 ; д)
; д) 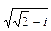 .
.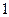 и
и  быть корнями какого-нибудь квадратного уравнения с действительными коэффициентами?
быть корнями какого-нибудь квадратного уравнения с действительными коэффициентами? .
. определена в некоторой окрестности точки
определена в некоторой окрестности точки  , кроме, быть может, самой точки
, кроме, быть может, самой точки  , если для любого сколь угодно малого ε > 0 найдется такое δ > 0, что
, если для любого сколь угодно малого ε > 0 найдется такое δ > 0, что  при
при 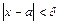 . Запись
. Запись 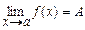 .
. в точке
в точке  существует, то он единственный.
существует, то он единственный. , если
, если  .
. называют бесконечно большой при
называют бесконечно большой при 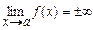 .
. .
. есть бесконечно большая функция и наоборот: если функция ƒ(x) – бесконечно большая, то
есть бесконечно большая функция и наоборот: если функция ƒ(x) – бесконечно большая, то  существуют, тогда
существуют, тогда  ;
;

 ;
;  .
. в точке
в точке  равен значению этого многочлена в точке
равен значению этого многочлена в точке  .
.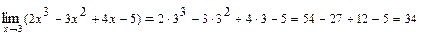 .
.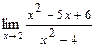 . Здесь пределы числителя и знаменателя равны 0, т. е. мы получили неопределенность
. Здесь пределы числителя и знаменателя равны 0, т. е. мы получили неопределенность  . Разложим на множители числитель и знаменатель дроби. Числитель разложим на множители по формуле
. Разложим на множители числитель и знаменатель дроби. Числитель разложим на множители по формуле  , где
, где  и
и  корни уравнения
корни уравнения  . Знаменатель разложим на множители по формуле
. Знаменатель разложим на множители по формуле 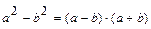 .
.  .
. . При
. При 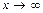 числитель и знаменатель дроби – бесконечно большие функции, т. е. дана неопределенность
числитель и знаменатель дроби – бесконечно большие функции, т. е. дана неопределенность  . Раскрывают такую неопределенность делением числителя и знаменателя дроби на наибольшую степень переменной знаменателя, в данном случае на
. Раскрывают такую неопределенность делением числителя и знаменателя дроби на наибольшую степень переменной знаменателя, в данном случае на  .
.  .
.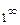 .
.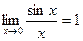 или
или 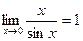 .
. или
или 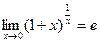 .
. .
. . Решение. Обозначим
. Решение. Обозначим 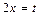 , тогда
, тогда  . Если
. Если  , то
, то  , а значит
, а значит  .
. .
. Решение. Сделаем замену переменной, полагая
Решение. Сделаем замену переменной, полагая  , тогда при
, тогда при  . Следовательно,
. Следовательно,  .
. Решение. Обозначим
Решение. Обозначим  , тогда
, тогда  . Если
. Если 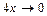 , а значит
, а значит  .
. .
. ».
». ; б)
; б)  ; в)
; в)  .
. ;
; .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б) 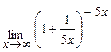 .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б)  .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б)  .
. ; б)
; б)  ; в)
; в)  .
.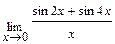 ; б)
; б) 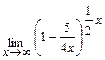 .
. ; б)
; б)  ; в)
; в)  .
.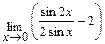 ; б)
; б)  .
. ?
? к приращению аргумента
к приращению аргумента  , когда приращение аргумента стремится к нулю:
, когда приращение аргумента стремится к нулю:  .
.
 ; 2.
; 2.  ; 3.
; 3.  ; 4.
; 4.  ; 5.
; 5. 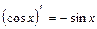 ; 6.
; 6.  ;7.
;7.  ; 8.
; 8. 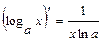 ; 9.
; 9.  ; 10.
; 10.  ; 11.
; 11. 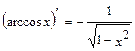 ; 12.
; 12. 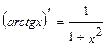 ; 13.
; 13.  ; 14.
; 14.  .
.
 , 2)
, 2) 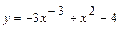 , 3)
, 3)  , 4 )
, 4 )  , 6)
, 6)  , 7)
, 7)  , 8)
, 8) 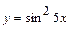 .
. . При вычислении производной перешли от корня к степени с рациональным показателем
. При вычислении производной перешли от корня к степени с рациональным показателем  , затем использовали правилом 5 и 1 формулой дифференцирования.
, затем использовали правилом 5 и 1 формулой дифференцирования.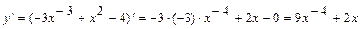 . При вычислении производной пользовались правилами 1, 3, 5 и 1 формулой дифференцирования.
. При вычислении производной пользовались правилами 1, 3, 5 и 1 формулой дифференцирования. . При вычислении производной пользовались правилом вычисления производной сложной функции и правилами 1, 3, 5, а также 1 формулой дифференцирования.
. При вычислении производной пользовались правилом вычисления производной сложной функции и правилами 1, 3, 5, а также 1 формулой дифференцирования.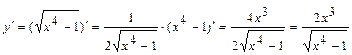 . При вычислении производной пользовались правилом вычисления производной сложной функции и правилами 1, 3, а также формулами дифференцирования 1 и 14.
. При вычислении производной пользовались правилом вычисления производной сложной функции и правилами 1, 3, а также формулами дифференцирования 1 и 14. . При вычислении производной пользовались правилом вычисления производной сложной функции и правилом 3 и 9 формулой дифференцирования.
. При вычислении производной пользовались правилом вычисления производной сложной функции и правилом 3 и 9 формулой дифференцирования. . При вычислении производной пользовались правилом вычисления производной сложной функции, 4 и 1 формулами дифференцирования. При упрощении результата пользовались формулой двойного аргумента
. При вычислении производной пользовались правилом вычисления производной сложной функции, 4 и 1 формулами дифференцирования. При упрощении результата пользовались формулой двойного аргумента  .
.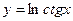 ; б)
; б) 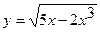 .
. ,
,  ; б)
; б) 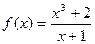 ,
,  ; в)
; в)  ,
,  ;
; ; б)
; б)  .
. ,
, 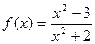 ,
, 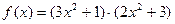 ,
,  ; б)
; б)  .
. ,
,  ,
,  ,
,  .
. ; б)
; б)  .
.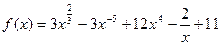 ,
,  ,
,  ,
,  ; б)
; б) 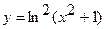 .
. ,
, 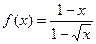 ,
,  ,
,  ; б)
; б)  .
.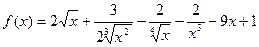 ,
,  ,
,  ,
,  в зависимости от времени дано уравнением
в зависимости от времени дано уравнением  А/с. Найти скорость изменения силы тока в конце десятой секунды.
А/с. Найти скорость изменения силы тока в конце десятой секунды. на монотонность и экстремумы.
на монотонность и экстремумы.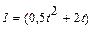 А/с. Найти скорость изменения силы тока в конце шестой секунды.
А/с. Найти скорость изменения силы тока в конце шестой секунды. на монотонность и экстремумы.
на монотонность и экстремумы. . С какой скоростью нагревается это тело в момент времени
. С какой скоростью нагревается это тело в момент времени 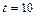 ?
? на монотонность и экстремумы.
на монотонность и экстремумы. . С какой скоростью нагревается это тело в момент времени
. С какой скоростью нагревается это тело в момент времени  ?
? на монотонность и экстремумы
на монотонность и экстремумы . Найти кинетическую энергию тела через 4 с после начала движения.
. Найти кинетическую энергию тела через 4 с после начала движения. подключеновнешнее сопротивление
подключеновнешнее сопротивление  . При каком
. При каком  и
и  ? Построить график мощности.
? Построить график мощности. . Найти кинетическую энергию тела через 2 с после начала движения.
. Найти кинетическую энергию тела через 2 с после начала движения. ) – параллельно. Определить при каком значении n батарея даст наибольший ток, если электродвижущая сила одного элемента Е, внутреннее сопротивление
) – параллельно. Определить при каком значении n батарея даст наибольший ток, если электродвижущая сила одного элемента Е, внутреннее сопротивление 


